660A - Взаимнопростый массив
Задача предложена пользователем Ali Ibrahim C137.
Заметим, что если есть пара соседних не взаимнопростых чисел, то мы обязаны между ними вставить какое-нибудь число. С другой стороны мы всегда можем вставить число 1.
Сложность: O(nlogn).
660B - Рассадка в автобусе
Задача предложена пользователем Srikanth Bhat bharsi.
В этой задаче нужно было сделать ровно то, что написано в условии. Никаких хитростей и подвохов.
Сложность: O(n).
660C - Сложный процесс
Задача предложена пользователем Mohammad Amin Raeisi Smaug.
Назовём отрезок [l, r] хорошим если в нём не более k ноликов. Заметим, что если отрезок [l, r] хороший, то отрезок [l + 1, r] тоже хороший. Таким образом, можно воспользоваться методом двух указателей: один указатель это l, а второй это r. Будем перебирать l слева направо и двигать r пока можем (для этого нужно просто поддерживать количество ноликов в текущем отрезке).
Сложность: O(n).
660D - Количество параллелограммов
Задачу предложена участником Sadegh Mahdavi smahdavi4.
Как известно диагонали параллелограмма делят друг друга пополам. Переберём пару точек a, b и рассмотрим середину отрезка 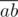 :
: 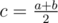 . Для всех середин отрезков посчитаем число cntc — количество пар точек, с этой серединой. Легко видеть, что ответ это
. Для всех середин отрезков посчитаем число cntc — количество пар точек, с этой серединой. Легко видеть, что ответ это 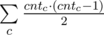 .
.
Сложность: O(n2logn).
660E - Различные подмножества по всем кортежам
Задача предложена пользователем Lewin Gan Lewin.
Рассмотрим некоторую подпоследовательность длины k > 0 (пустые подпоследовательности можно учесть отдельно, прибавив в конце к ответу число mn) и посчитаем количество последовательностей в которых она будет учтена. Нам это нужно сделать аккуратно, чтобы всё посчитать ровно по одному разу. Пусть x1, x2, ... , xk это наша подпоследовательность. Тогда в исходной последовательности перед элементом x1 могли находиться ещё числа, но число x1 не могло встретиться (поскольку мы хотим всё посчитать по разу, варианты когда x1 уже встречалось нам не нужно учитывать). Таким образом, у нас (m - 1) вариант для каждого из чисел перед x1. Аналогичо, между числами x1 и x2 могут находиться некоторые числа (но не может находиться число x2). И так далее. После числа xk может находиться ещё некоторое количество чисел (пусть их j штук), причём на них не накладывается никаких ограничений (то есть m вариантов для каждого числа). Мы зафиксировали, что в конце стоит j чисел, значит n - k - j чисел нужно распределить между числами перед x1, между x1 и x2, \ldots , между xk - 1 и xk. Легко видеть, что это можно сделать 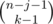 способами (это просто биномиальный коэффициент с повторениями). Количество последовательностей x1, x2, ... , xk, конечно, равно mk. Таким образом, ответ это
способами (это просто биномиальный коэффициент с повторениями). Количество последовательностей x1, x2, ... , xk, конечно, равно mk. Таким образом, ответ это 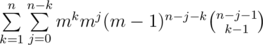 . Последнюю сумму легко преобразовать к виду
. Последнюю сумму легко преобразовать к виду 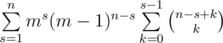 . Заметим, что последняя внутренняя сумма легко суммируется с помощью известной формулы параллельного суммирования:
. Заметим, что последняя внутренняя сумма легко суммируется с помощью известной формулы параллельного суммирования: 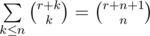 . Таким образом, ответ равен:
. Таким образом, ответ равен: 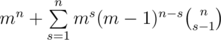 . Можно далее сворачивать сумму, чтобы получить логарифмическое решение (закнутую формулу), но в задаче это не требовалось.
. Можно далее сворачивать сумму, чтобы получить логарифмическое решение (закнутую формулу), но в задаче это не требовалось.
Сложность: O((n + m)log MOD), где MOD = 109 + 7.
660F - Медведь и боулинг 4
Задача предложена пользователем Kamil Debowski Errichto.
Далее приводится разбор моего решения. Также вы можете посмотреть разбор от автора задачи в английском треде.
Применим метод разделяй и властвуй. Рассмотрим отрезок [l, r] и найдём в нём подотрезок с максимальной взвешенной суммой. Для этого разобьём отрезок на две части [l, md - 1] и [md, rg], где 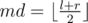 . Согласно методу разделяй и властвуй посчитаем рекурсивно ответ, если он лежит целиком в левой или правой половине. Теперь нужно учесть отрезки, пересекающие середину. Рассмотрим некоторый отрезок [i, j], i < md, md ≤ j. Взвешенная сумма на ней равна:
. Согласно методу разделяй и властвуй посчитаем рекурсивно ответ, если он лежит целиком в левой или правой половине. Теперь нужно учесть отрезки, пересекающие середину. Рассмотрим некоторый отрезок [i, j], i < md, md ≤ j. Взвешенная сумма на ней равна: 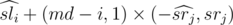 , где
, где 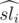 --- взвешенная сумма в подотрезке [i, md],
--- взвешенная сумма в подотрезке [i, md], 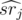 — взвешенная сумма на подотрезке [md + 1, r], а srj — просто сумма на подотрезке [md + 1, r]. Знак × применяется в смысле геометрического псевдовекторного произведения. Таким образом, у нас есть набор векторов вида (md - i, 1) и некоторый набор точек и для каждого вектора первого набора нужно найти точку из второго набора, максимизирующую значение векторного произведения. Это легко сделать, построив выпуклую оболочку по множеству точек и далее, двигая указатель по выпуклой оболочке.
— взвешенная сумма на подотрезке [md + 1, r], а srj — просто сумма на подотрезке [md + 1, r]. Знак × применяется в смысле геометрического псевдовекторного произведения. Таким образом, у нас есть набор векторов вида (md - i, 1) и некоторый набор точек и для каждого вектора первого набора нужно найти точку из второго набора, максимизирующую значение векторного произведения. Это легко сделать, построив выпуклую оболочку по множеству точек и далее, двигая указатель по выпуклой оболочке.
Обратите внимание, что в данном решении есть проблема переполнения значений векторного произведения. Эту проблему можно обойти, если сначала сравнивать значение векторного произведения в типе long double или double и только потом в типе long long. Оригинальное решение автора задачи не имеет такой проблемы.
Сложность: O(nlog2n).











We don't need divide and conquer in F. We can use only convex hull trick. This way the solution has better complexity and is easier to implement.
Let's say that S1 is a normal prefix sum array, that is S1[i]=A[1]+A[2]+...+A[i] and S2 is again a prefix sum array but this time every element is multiplied by its index, that is S2[i]=A[1]+2*A[2]+3*A[3]+...+i*A[i]. Let's choose some R which will be the right end of our chosen interval. Now we are looking for the L that minimizes S2[R]-S2[L-1]-(L-1)*(S1[R]-S1[L-1]) which is a standard use of CHT — http://codeforces.net/contest/660/submission/17245184.
The complexity is O(NlogN).
Nice! And is it possible to implement it with integers only?
Ah yes, since we need to compare A1/B1 and A2/B2 where A1, B1, A2 and B2 are integers. Thanks if you asked to make me think about it, I will know that in future! :)
But I think your B may be up to N2·107 and A is up to N·107 so long long's won't be enough to multiply them. So maybe the intended solution was valuable anyway because it allowed to use integers only.
Oh yeah, they are too big, sorry. But don't think that I want to say it's not valuable, of course it is.
In a previous educational round we've learnt how to compare fractions of long longs in integers http://codeforces.net/blog/entry/21588?#comment-262867
sum_so_far can be N * 107
score_so_far can be N2 * 107
When we will calculate f.a*f.b it can be N3 * 107, which is bigger than 1022.
Am I missing something?
f.a is up to N and f.b is up to N2·107 but we don't multiply some random values. Values of f.a increase by 1 and values of f.b increase by N·107, as we move from fi to fi + 1 (and we multiply differences like f1.a - f2.a). I came up with a proof that it amortizes but I don't see that proof right now. I will try to get it again (and I hope it exists).
My approach for
Problem Fis as follow (It didn't work, but I can't find the bug in this algorithm):We can determine the stop point (deleted suffix) by looping back from
nto1:then I implemented this for loop to get the best stop point for every
i:So now
go[i]+1--->nwill be the deleted suffix for itemi.I think if this part of code works , I think this problem can be solved in
O(n)Complexity, And if it doesn't work, my approach will fail entirely.So, what is wrong with my code?
In C problem, why complexity O(n + k)? even if k > n it will be O(n).
Well technically you are right.
Anyway considering the fact, that (by the statement) K<=N, then O(n+k) == O(n) (the complexities are equal)
So → you are right, but so is Edvard (at least in asymptote) ^_^
But I agree that it might be slightly misleading, considering, that the "k" really does not have to be used for counting of the complexity :)
Thanks. Fixed.
For D, another interpretation is to count pairs (dx, dy) for all pairs of points and then for each such pair add to answer count * (count - 1) / 2. Since the parallel sides are parallel and has same length. But we will count each parallelogram twice, so divide the answer by 2.
It's just a building vectors on each parallelogram's side, isn't it?
an easier aproach and easy to implement is to find miidle of each line then use the fact that in every parallogram diagonals intersect at the middle.
It will be not working if more than 3 points can lie on the same line. For example, {(2,2),(4,4),(-2,-2),(-4,-4)} is not a parallelogram. Yes, I know, following by problem statement it`s impossible, but the fact remains.
exactly as you say!
Build vectors, merge them (count number of same vectors) and use Gauss's formula!
^_^
Названия задач E и F не из этого контеста. Копипаста-с :)
Спасибо. Поправил.
How can you solve Problem E?
I could not understand the editorial. Can someone please explain?
Out of A,B,C,D guess which one I found the hardest? That's right! A. FML ;_;
There is another method of solving B with sorting. Some people might find it easier and shorter to code
17235532
For Problem F you can just make a form of slope such that (p[j] — p[k]) / (j — k) <= s[i], where p[i] = i * sigma(a[i]) — sigma(i * a[i]), s[i] = sigma(a[i]). then you can make a convex hull, for each i, you just to use binary search to find the best choice and update the answer. this complexity is O(nlogn)
for E ,in 5th line ,there should be m - 1 choices for each of them but not k-1 choices.
Thanks. Fixed.
Here's just a funny story I want to tell you guys.
I solved problem F by a weird O(N) algorithm, which is not correct.
http://codeforces.net/contest/660/submission/17264773 (Accepted)
Maybe test cases are weak, so my solution passed 52/54 tests (failed on 2 tests, I had to write "if n=... cout..." in order to AC). Seem crazy right ?
An O(n) alternative for E:
This is more direct from the statement of the problem. We build the set of all sequences, element by element, from left to right, and
currenttracks the count of distinct subsequences within all the sequences (visualise a different room for each sequence maybe). At each step for each room we createmnew rooms. Also, in each room, each subsequence splits into two: one with the newly added element, and one without. Except we have just created some subsequences that were already there; all of them, in fact (except the empty ones), so we subtract them (the number of empty ones ispowr, which ism**i).Seems to work: 17242031.
It seems I forgot how to solve recurrences. But Wolfram Alpha hasn't. Edit: for some reason that link doesn't work. Here it is: https://www.wolframalpha.com/input/?i=solve+recurrence+a%5Bi%5D+%3D+a%5Bi-1%5D*K+%2B+M%5E%28i-1%29
So there's a O(lg (n+m+MOD)) solution. Logarithmic time means we can solve it in Python!
Complete solution:
Apparently it works: 17273456
Hey,this may be a bit naive question but please can you explain how the answer for n=2 & m=2 for this problem is 14.
There are 4 sequences and in each we need to count unique subsequences:
00: [], [0], [0,0]
01: [], [0], [1], [0,1]
10: [], [0], [1], [1,0]
11: [], [1], [1,1]
That's 3+4+4+3.
For B, you say "There are no tricks." What about 17246985?
thank you)
I don't understand why the problem D is complexity O(n^2*logn), I know that the n^2 is there because we have to compare every segment with every other segment but I don't understand why the log(n).
The log(n) comes up from the complexity of the data structure needed to handle cnt, such as a C++ map. Note that you need to count how many times a point appears as a middle point.
Кину камень в огород человеку, писавшему решения.
Что это за "магические" define, которые не добавлены в решение?
Неужели было так трудно написать нормально циклы?
I didnt understand the samples in the question for E, could someone help me out here?
Can someone elaborate on the following from problem E's editorial?
+1
4 years later, you finally get your answer! :D
Claim 1:
$$$\sum_{k=1}^{n}{\sum_{j = 0}^{n - k}{m^km^j(m - 1)^{n - j - k}{n - j - 1 \choose k - 1}}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{k = 0}^{s - 1}{n - s + k \choose k}}$$$
Proof:
We have:
$$$\sum_{k=1}^{n}{\sum_{j = 0}^{n - k}{m^km^j(m - 1)^{n - j - k}{n - j - 1 \choose k - 1}}} = \sum_{k = 1}^{n}{\sum_{j = 0}^{n - k}{m^{k + j}(m - 1)^{n - (k + j)}{n - j - 1 \choose k - 1}}}$$$
Observe that the quantity $$$k + j$$$ appears in most of the members of the inner multiplication, so summing over it in the outer sigma would simply the sum. Let $$$s = j + k$$$. Instead of summing over $$$k$$$ in the outer and $$$j$$$ in the inner, let's sum over all of the values of $$$s$$$ in the outer and $$$j$$$ in the inner, and the corresponding value of $$$k$$$ will be $$$s - j$$$.
This is useful because $$$m^{k + j}(m-1)^{n - (k + j)}$$$ will turn into $$$m^{s}(m - 1)^{n - s}$$$ and we can take that quantity outside of the inner sum because it's independent of $$$j$$$. Also, note that the minimum value for $$$s$$$ is $$$1 + 0 = 1$$$, and the maximum value for $$$s$$$ is simply $$$n$$$. Finally, note that when fixing $$$s$$$, $$$j$$$'s possible range is $$$[0, s - 1]$$$, as $$$k$$$'s possible range is $$$[1, s]$$$ and $$$j = s - k$$$.
So we get: $$$\sum_{k = 1}^{n}{\sum_{j = 0}^{n - k}{m^{k + j}(m - 1)^{n - (k + j)}{n - j - 1 \choose k - 1}}} = \sum_{s = 1}^{n}{\sum_{j = 0}^{s - 1}{m^s(m - 1)^{n - s}{n - j - 1 \choose s - j - 1}}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{j = 0}^{s - 1}{n - j - 1 \choose s - j - 1}}$$$
Now we have to deal with the inner creature, $$$\sum_{j = 0}^{s - 1}{n - j - 1 \choose s - j - 1}$$$. Let $$$k$$$ (note that this is NOT the $$$k$$$ from before, this is simply bad variable name choice) be $$$s - j - 1$$$. we want to sum over all values of this $$$k$$$ instead all values of $$$j$$$. obsevre that based on the definition we gave for $$$k$$$, $$$j = s - k - 1$$$, and because the range for $$$j$$$ is $$$[0, s - 1]$$$, the range for $$$k$$$ will be $$$[0, s-1]$$$ (because when $$$j$$$ is $$$0$$$ $$$k$$$ will be $$$s - 1$$$ and when $$$j$$$ is $$$s - 1$$$, $$$k$$$ will be $$$0$$$ (we did a similar thing when converting to summing over $$$s$$$)).
We get: $$$\sum_{j = 0}^{s - 1}{n - j - 1 \choose s - j - 1} = \sum_{k = 0}^{s - 1}{n - (s - k - 1) - 1 \choose k} = \sum_{k = 0}^{s - 1}{n - s + k \choose k}$$$
Finally, substituting and combining everything: $$$\sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{j = 0}^{s - 1}{n - j - 1 \choose s - j - 1}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{k = 0}^{s - 1}{n - s + k \choose k}}$$$.
To conclude, coming back to the initial equality we found: $$$\sum_{k=1}^{n}{\sum_{j = 0}^{n - k}{m^km^j(m - 1)^{n - j - k}{n - j - 1 \choose k - 1}}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{k = 0}^{s - 1}{n - s + k \choose k}}$$$, as desired. $$$\blacksquare$$$
Claim 2:
$$$\sum_{k = 0}^{s - 1}{n - s + k \choose k} = {n \choose s-1}$$$
Proof:
Introducing: The Hockey-Stick Identity
Our intuition is to use the Hockey-Stick Identity. The Mirror-Image Hockey-Stick Identity is stated as follows (specifically MHS & RHS of it in Wikipedia): $$$\sum_{k = 0}^{n - r}{k + r \choose k} = {n+1 \choose n-r}$$$ (note that $$$n \ge r$$$ must be satisfied).
We have $$$k$$$ in the bottom part of the choose, so the thing added to it, $$$r$$$, should be the upper part of the choose in the summation minus $$$k$$$, namely, let $$$r = n - s$$$. also, let the $$$n$$$ from the Hockey-Stick identity $$$n - 1$$$ (where this $$$n$$$ is the length of the sequence). Note that $$$n - 1 \ge n - s$$$ therefore the $$$n \ge r$$$ condition is satisfied.
Substituting: (HockeyStick($$$r = n - s$$$, $$$n = n - 1$$$))
$$$\sum_{k = 0}^{n - 1 - (n - s)}{k + n - s \choose k} = {n - 1 + 1 \choose n - 1 - (n - s)} \implies \sum_{k = 0}^{s - 1}{n - s + k \choose k} = {n \choose s-1}$$$, as desired. $$$\blacksquare$$$
Substituting into Claim 1:
$$$\sum_{k=1}^{n}{\sum_{j = 0}^{n - k}{m^km^j(m - 1)^{n - j - k}{n - j - 1 \choose k - 1}}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}{n \choose s-1}}$$$
And now, the only thing left is to include the empty sequence, we should count every sequence of length $$$n$$$, and there are $$$m$$$ options for each position therefore $$$m^n$$$ such sequences therefore we arrive at our final answer:
$$$m^n + \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}{n \choose s-1}}$$$ $$$\square$$$
I will need to go back to this problem again lol. Thanks for writing this down!
You're welcome! :)
Once you finish reading & upsolving, please update here, I wrote this explanation in 2 AM and error checking would be cool :p
The closed formula being referred to in problem E is:
$$$ans = m^n + \frac{m}{m-1}((2m-1)^n - m^n)$$$.
It doesn't work when $$$m = 1$$$ (because of division by 0). But in that case, since there is only a single sequence of length $$$n$$$ comprising of all $$$1$$$-s, the answer is simply $$$(n + 1)$$$.
A note for Problem E: Different Subsets For All Tuples
What got me stuck on the problem is that I initially considered the sequence x1, x2 .. xk but I said xi cant appear in the range (position of xi-1, position of xi+1), but that completely ignored cases in which the value appears multiple times in the same segment.
So usually, in combinatorics we like to rephrase things and identify things, so the idea for cases in which the sequence appears multiple times is to only consider the sequence with the smallest lexicographical position vector. this is what allows for the described approach.
Since math is hard, I have a solution for $$$E$$$ which requires basically no math and is really easy to implement! I can't prove the correctness of it in any nice way.
So first is to try out small $$$(n, m)$$$ and brute force the answers, probably using some computer program or something. That way, we can try to find a pattern.
If you put this in a table, we get:
2 4 6 8 10 12
3 14 33 60 95 138
4 46 174 436 880 1554
5 146 897 3116 8045 17310
6 454 4566 22068 73030 191706
I index the table such that the column index represents $$$m$$$ and the row index represent $$$n$$$.
Let's read the table column by column. The third column is:
6 33 174 897 4566
Notice that everything seems to be around $$$5$$$ times bigger than the previous number. There's a little bit of an offset, though. The offsets are powers of $$$3$$$.
The fourth column:
8 60 436 3116 22068
Notice that everything seems to be around $$$7$$$ times bigger than the previous number. There's a bit of an offset, by powers of $$$4$$$.
And that's the main observation.
$$$\boxed{f(n, m) = f(n - 1, m) \cdot (2 \cdot m + 1) + m^{n - 1}}.$$$
Easy to constructive recursive solution from there.
DP solution for Problem E:
For a specific sequence $$$a_1, a_2, a_3, ... $$$, it's known that $$$dp[i] = dp[i-1] * 2 - dp[j-1]$$$ in which $$$j$$$ is the latest position that $$$a_j = a_i$$$.
Now, let $$$dp[i]$$$ represent the sum of $$$dp[i]$$$ sequence whose last element is specific $$$x$$$. $$$x$$$ may be any number between $$$1$$$ to $$$m$$$, but it doesn't matter. $$$dp[i] = dp[i-1] * m * 2$$$ is hold for every sequence. And we should subject some $$$dp[j]$$$ from it. We can iterator the latest $$$j$$$, count the number, so we can get:
$$$dp[i] = dp[i-1] * 2 - \sum_j dp[j-1] * m * {(m-1)}^{i-j-1} $$$
And the sum is very easy to maintain when we loop it.
146751249
Here's insight into "parallel summing" in problem e solution: https://codeforces.net/blog/entry/104172