→ Languages
The following languages are only available languages for the problems from the contest
Microsoft Q# Coding Contest - Summer 2018:
- Microsoft Q#
→ Virtual participation
Virtual contest is a way to take part in past contest, as close as possible to participation on time. It is supported only ICPC mode for virtual contests.
If you've seen these problems, a virtual contest is not for you - solve these problems in the archive.
If you just want to solve some problem from a contest, a virtual contest is not for you - solve this problem in the archive.
Never use someone else's code, read the tutorials or communicate with other person during a virtual contest.
→ Problem tags
*special problem
*1500
No tag edit access
→ Contest materials
The problem statement has recently been changed. View the changes.
×
E1. Bernstein-Vazirani algorithm
time limit per test
2 secondsmemory limit per test
256 megabytesinput
standard inputoutput
standard outputYou are given a quantum oracle - an operation on N + 1 qubits which implements a function 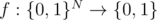 . You are guaranteed that the function f implemented by the oracle is scalar product function (oracle from problem D1):
. You are guaranteed that the function f implemented by the oracle is scalar product function (oracle from problem D1):
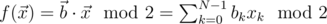
Here 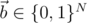 (an array of N integers, each of which can be 0 or 1).
(an array of N integers, each of which can be 0 or 1).
Your task is to reconstruct the array 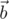 . Your code is allowed to call the given oracle only once.
. Your code is allowed to call the given oracle only once.
You have to implement an operation which takes the following inputs:
- an integer N - the number of qubits in the oracle input (1 ≤ N ≤ 8),
- an oracle Uf, implemented as an operation with signature ((Qubit[], Qubit) => ()), i.e., an operation which takes as input an array of qubits and an output qubit and has no output.
The return of your operation is an array of integers of length N, each of them 0 or 1.
Your code should have the following signature:
namespace Solution {
open Microsoft.Quantum.Primitive;
open Microsoft.Quantum.Canon;
operation Solve (N : Int, Uf : ((Qubit[], Qubit) => ())) : Int[]
{
body
{
// your code here
}
}
}
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/27/2025 03:59:47 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|



