- Microsoft Q#
You are given a quantum oracle - an operation on N + 1 qubits which implements a function 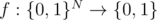 . You are guaranteed that the function f implemented by the oracle can be represented in the following form (oracle from problem D2):
. You are guaranteed that the function f implemented by the oracle can be represented in the following form (oracle from problem D2):
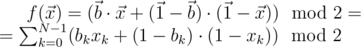
Here 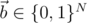 (a vector of N integers, each of which can be 0 or 1), and
(a vector of N integers, each of which can be 0 or 1), and 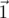 is a vector of N 1s.
is a vector of N 1s.
Your task is to reconstruct the array 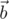 which could produce the given oracle. Your code is allowed to call the given oracle only once.
which could produce the given oracle. Your code is allowed to call the given oracle only once.
You have to implement an operation which takes the following inputs:
- an integer N - the number of qubits in the oracle input (1 ≤ N ≤ 8),
- an oracle Uf, implemented as an operation with signature ((Qubit[], Qubit) => ()), i.e., an operation which takes as input an array of qubits and an output qubit and has no output.
The return of your operation is an array of integers of length N, each of them 0 or 1.
Note that in this problem we're comparing the oracle generated by your return to the oracle Uf, instead of comparing your return to the (hidden) value of 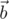 used to generate Uf. This means that any kind of incorrect return results in "Runtime Error" verdict, as well as actual runtime errors like releasing qubits in non-zero state.
used to generate Uf. This means that any kind of incorrect return results in "Runtime Error" verdict, as well as actual runtime errors like releasing qubits in non-zero state.
Your code should have the following signature:
namespace Solution {
open Microsoft.Quantum.Primitive;
open Microsoft.Quantum.Canon;
operation Solve (N : Int, Uf : ((Qubit[], Qubit) => ())) : Int[]
{
body
{
// your code here
}
}
}
| Name |
|---|



