| VK Cup 2019 - Квалификация (Engine) |
|---|
| Finished |
Для надежного, но компактного хранения картинок во ВКонтакте используются избыточные коды. Все картинки разбиваются на группы по 15, и для каждой группы картинок вычисляются 13 избыточных кодов. Избыточные коды необходимы, чтобы суметь восстановить некоторые картинки, если они будут утеряны вследствие поломки жесткого диска.
Перед вычислением избыточных кодов 15 картинок из одной группы записываются в матрицу из 3 строк и 5 столбцов. Далее к получившейся матрице справа добавляются два столбца с 6 избыточными кодами (каждая пара кодов вычисляется на основе картинок в той же строке), а затем снизу добавляется еще одна строка из 7 избыточных кодов (каждый из них считается на основе картинок или избыточных кодов в том же столбце).
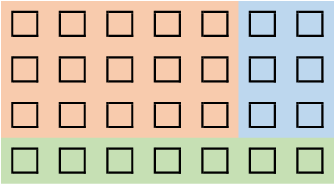
Будем называть картинки и избыточные коды блоками. Таким образом, из 15 картинок мы получили 28 блоков, расставленных в виде матрицы 4 на 7. В данной задаче вам не будут даны формулы вычисления избыточных кодов, но даны их свойства: а именно по 3 любым блокам из одного столбца можно однозначно восстановить утерянный четвертый блок в том же столбце, а также по 5 любым блокам из одной строки можно однозначно восстановить оставшиеся два из той же строки, если они были утеряны. Естественно, операцию восстановления можно применять несколько раз к разным строкам и столбцам в любом порядке, а также в следующих операциях использовать блоки, восстановленные ранее.
Пусть у вас есть 28 блоков (15 картинок и 13 избыточных кодов), и вы потеряли случайные $$$k$$$ из них (равновероятно среди всех вариантов). Ваша задача посчитать вероятность, что хотя бы одну из 15 картинок будет невозможно восстановить, а также матожидание количества потерянных картинок.
В единственной строке входных данных записано целое число $$$k$$$ ($$$0 \le k \le 28$$$) — количество потерянных блоков.
Выведите два числа — вероятность, что хотя бы одну картинку невозможно восстановить из оставшихся блоков, и матожидание количества картинок, которые невозможно восстановить из оставшихся блоков.
Ответы будут считаться корректными, если их абсолютная или относительная погрешность не превосходит $$$10^{-9}$$$.
28
1.00000000000000000000 15.00000000000000000000
6
0.00055741360089186175 0.00179168657429526999
В первом примере утеряны все 28 блоков, очевидно, с 100% вероятностью потеряны все 15 картинок.
Во втором примере только в 210 случаев из 376740 будет невозможно восстановить хотя бы одну картинку, поэтому вероятность $$$210/376740$$$. В зависимости от расположения утерянных блоков будет невозможно восстановить от 1 до 6 картинок, матожидание равно $$$15/8372$$$.
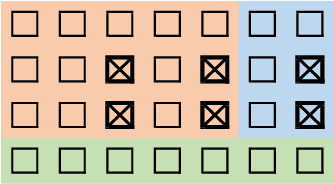
Приведены два возможных способа потерять 6 блоков.
На первом случае утеряны 3 картинки и 3 избыточных кода (отмечены крестиками). Вначале мы можем восстановить один утерянный блок в первой строке (используя 5 других из этой же строки) и восстановить два утерянных блока в четвертой строке (используя 5 других из той же строки). Затем мы можем восстановить три оставшихся блока (используя 3 других блока из соответствующих столбцов). Заметим, что при восстановлении по столбцу мы использовали в том числе и восстановленные на первом шаге блоки. Таким образом, нам удалось восстановить все блоки и не было потеряно ни одной картинки.

На втором случае утеряны 4 картинки и 2 избыточных кода. Во второй и третьей строках по три утерянных блока, а значит мы не можем однозначно восстановить ни один из блоков в них. Аналогично, в третьем, пятом и седьмом столбцах по два утерянных блока, а значит мы не можем однозначно восстановить ни один из блоков в них. В остальных строках и столбцах все блоки остались целыми, восстанавливать нечего. Таким образом, нам не удастся восстановить ни один из шести утерянных блоков, но только из четыре из них были картинками.
| Name |
|---|




