This problem is split into two tasks. In this task, you are required to find the minimum possible answer. In the task Village (Maximum) you are required to find the maximum possible answer. Each task is worth $$$50$$$ points.
There are $$$N$$$ houses in a certain village. A single villager lives in each of the houses. The houses are connected by roads. Each road connects two houses and is exactly $$$1$$$ kilometer long. From each house it is possible to reach any other using one or several consecutive roads. In total there are $$$N-1$$$ roads in the village.
One day all villagers decided to move to different houses — that is, after moving each house should again have a single villager living in it, but no villager should be living in the same house as before. We would like to know the smallest possible total length in kilometers of the shortest paths between the old and the new houses for all villagers.
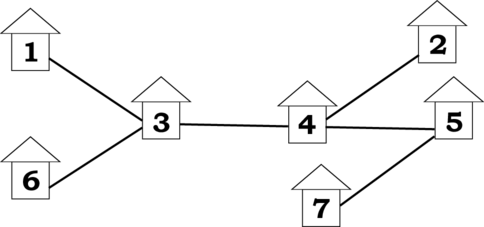
Example village with seven houses
For example, if there are seven houses connected by roads as shown on the figure, the smallest total length is $$$8$$$ km (this can be achieved by moving $$$1 \to 6$$$, $$$2 \to 4$$$, $$$3 \to 1$$$, $$$4 \to 2$$$, $$$5 \to 7$$$, $$$6 \to 3$$$, $$$7 \to 5$$$).
Write a program that finds the smallest total length of the shortest paths in kilometers and an example assignment of the new houses to the villagers.
The first line contains an integer $$$N$$$ ($$$1 < N \le 10^5$$$). Houses are numbered by consecutive integers $$$1, 2, \ldots, N$$$.
Then $$$N-1$$$ lines follow that describe the roads. Each line contains two integers $$$a$$$ and $$$b$$$ ($$$1 \le a, b \le N$$$, $$$a \neq b$$$) denoting that there is a road connecting houses $$$a$$$ and $$$b$$$.
In the first line output the smallest total length of the shortest paths in kilometers.
In the second line describe one valid assignment of the new houses with the smallest total length: $$$N$$$ space-separated distinct integers $$$v_1, v_2, \ldots, v_N$$$. For each $$$i$$$, $$$v_i$$$ is the house number where the villager from the house $$$i$$$ should move ($$$v_i \neq i$$$). If there are several valid assignments, output any of those.
Subtasks:
- (6 points) $$$N \leq 10$$$
- (19 points) $$$N \leq 1\,000$$$
- (25 points) No further constraints
4 1 2 2 3 3 4
4 2 1 4 3
7 4 2 5 7 3 4 6 3 1 3 4 5
8 3 4 6 2 7 1 5
| Name |
|---|




