| Codeforces Round 791 (Div. 2) |
|---|
| Finished |
You have a square chessboard of size $$$n \times n$$$. Rows are numbered from top to bottom with numbers from $$$1$$$ to $$$n$$$, and columns — from left to right with numbers from $$$1$$$ to $$$n$$$. So, each cell is denoted with pair of integers $$$(x, y)$$$ ($$$1 \le x, y \le n$$$), where $$$x$$$ is a row number and $$$y$$$ is a column number.
You have to perform $$$q$$$ queries of three types:
- Put a new rook in cell $$$(x, y)$$$.
- Remove a rook from cell $$$(x, y)$$$. It's guaranteed that the rook was put in this cell before.
- Check if each cell of subrectangle $$$(x_1, y_1) - (x_2, y_2)$$$ of the board is attacked by at least one rook.
Subrectangle is a set of cells $$$(x, y)$$$ such that for each cell two conditions are satisfied: $$$x_1 \le x \le x_2$$$ and $$$y_1 \le y \le y_2$$$.
Recall that cell $$$(a, b)$$$ is attacked by a rook placed in cell $$$(c, d)$$$ if either $$$a = c$$$ or $$$b = d$$$. In particular, the cell containing a rook is attacked by this rook.
The first line contains two integers $$$n$$$ and $$$q$$$ ($$$1 \le n \le 10^5$$$, $$$1 \le q \le 2 \cdot 10^5$$$) — the size of the chessboard and the number of queries, respectively.
Each of the following $$$q$$$ lines contains description of a query. Description begins with integer $$$t$$$ ($$$t \in \{1, 2, 3\}$$$) which denotes type of a query:
- If $$$t = 1$$$, two integers $$$x$$$ and $$$y$$$ follows ($$$1 \le x, y \le n$$$) — coordinated of the cell where the new rook should be put in. It's guaranteed that there is no rook in the cell $$$(x, y)$$$ at the moment of the given query.
- If $$$t = 2$$$, two integers $$$x$$$ and $$$y$$$ follows ($$$1 \le x, y \le n$$$) — coordinates of the cell to remove a rook from. It's guaranteed that there is a rook in the cell $$$(x, y)$$$ at the moment of the given query.
- If $$$t = 3$$$, four integers $$$x_1, y_1, x_2$$$ and $$$y_2$$$ follows ($$$1 \le x_1 \le x_2 \le n$$$, $$$1 \le y_1 \le y_2 \le n$$$) — subrectangle to check if each cell of it is attacked by at least one rook.
It's guaranteed that among $$$q$$$ queries there is at least one query of the third type.
Print the answer for each query of the third type in a separate line. Print "Yes" (without quotes) if each cell of the subrectangle is attacked by at least one rook.
Otherwise print "No" (without quotes).
8 10 1 2 4 3 6 2 7 2 1 3 2 3 6 2 7 2 1 4 3 3 2 6 4 8 2 4 3 3 2 6 4 8 1 4 8 3 2 6 4 8
No Yes Yes No Yes
Consider example. After the first two queries the board will look like the following picture (the letter $$$R$$$ denotes cells in which rooks are located, the subrectangle of the query of the third type is highlighted in green):

Chessboard after performing the third and the fourth queries:

Chessboard after performing the fifth and the sixth queries:
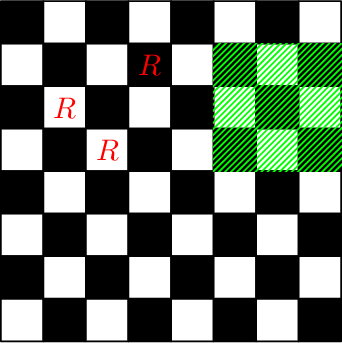
Chessboard after performing the seventh and the eighth queries:
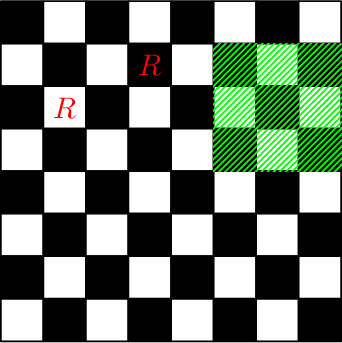
Chessboard after performing the last two queries:
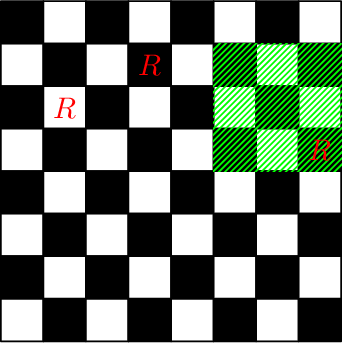
| Name |
|---|




