| 2022-2023 ICPC, NERC, Northern Eurasia Onsite (Unrated, Online Mirror, ICPC Rules, Teams Preferred) |
|---|
| Finished |
Emma loves playing with blocks. She has several cubic blocks of the same size that are numbered with distinct integers written on them. She assembles towers from those blocks by stacking them vertically.
A configuration of her game is a set of towers that she has assembled from the blocks. Emma can perform two kinds of operations on a configuration of towers:
- Split any tower with more than one block in it by taking any number of blocks from the top of the tower and moving them to a new tower keeping their order, so that the top block of the old tower becomes the top block of the new tower. As a result of this operation, the number of towers increases by one.
- Combine any two towers by moving blocks from one tower on top of the other tower in the same order. As a result of this operation, the number of towers decreases by one.
Emma wants to stack all the blocks into a single tower so that all blocks come in order sorted by the numbers — from the block with the minimal number at the top to the block with the maximal number at the bottom. Emma wants to do as little of splitting and combining operations as possible. Your task is to find the minimal number of operations she has to make and output how many splits and combines are needed.
The first line of the input file contains an integer $$$n$$$ ($$$1 \le n \le 10\,000$$$) — the number of towers in the initial configuration. Next $$$n$$$ lines describe towers. Each tower $$$i$$$ is described by a line that starts with the number $$$k_i$$$ ($$$k_i \ge 1$$$; $$$\sum_1^n{k_i} \le 10\,000$$$) — the number of blocks in the tower, followed by $$$k_i$$$ numbers $$$b_{i,j}$$$ ($$$1 \le b_{i,j} \le 10^9$$$) — numbers written on the blocks in the $$$i$$$-th tower, listed from top to bottom. All block numbers listed in the input are different.
Output a line with two integers $$$s$$$ and $$$c$$$ — the number of split and combine operations Emma should make to get a single tower with blocks sorted by their numbers, so that the total number of operations is minimized.
2 3 3 5 8 2 9 2
1 2
The example needs the following operations (1 split and 2 combines).
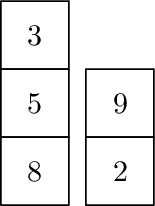 | 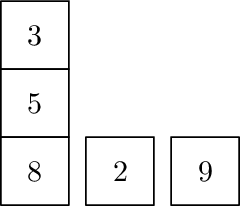 | 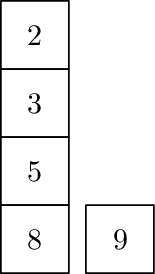 |  |
| Initial | Split last | Combined 2nd onto 1st | Combined 1st onto 2nd |
| Name |
|---|




