You are given a tree with $$$n$$$ nodes labelled $$$1,2,\dots,n$$$. The $$$i$$$-th edge connects nodes $$$u_i$$$ and $$$v_i$$$ and has an unknown positive integer weight $$$w_i$$$. To help you figure out these weights, you are also given the distance $$$d_i$$$ between the nodes $$$i$$$ and $$$i+1$$$ for all $$$1 \le i \le n-1$$$ (the sum of the weights of the edges on the simple path between the nodes $$$i$$$ and $$$i+1$$$ in the tree).
Find the weight of each edge. If there are multiple solutions, print any of them. If there are no weights $$$w_i$$$ consistent with the information, print a single integer $$$-1$$$.
The first line contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$).
The $$$i$$$-th of the next $$$n-1$$$ lines contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i,v_i \le n$$$, $$$u_i \ne v_i$$$).
The last line contains $$$n-1$$$ integers $$$d_1,\dots,d_{n-1}$$$ ($$$1 \le d_i \le 10^{12}$$$).
It is guaranteed that the given edges form a tree.
If there is no solution, print a single integer $$$-1$$$. Otherwise, output $$$n-1$$$ lines containing the weights $$$w_1,\dots,w_{n-1}$$$.
If there are multiple solutions, print any of them.
5 1 2 1 3 2 4 2 5 31 41 59 26
31 10 18 8
3 1 2 1 3 18 18
-1
9 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 2 236 205 72 125 178 216 214 117
31 41 59 26 53 58 97 93
In the first sample, the tree is as follows:
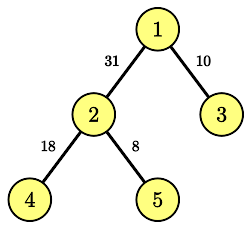
In the second sample, note that $$$w_2$$$ is not allowed to be $$$0$$$ because it must be a positive integer, so there is no solution.
In the third sample, the tree is as follows:
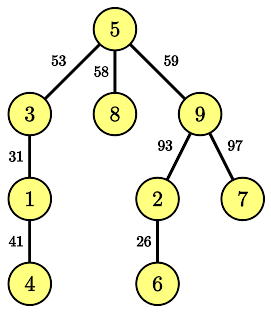
| Name |
|---|




