| Codeforces Round 924 (Div. 2) |
|---|
| Finished |
Bob has a rectangle of size $$$a \times b$$$. He tries to cut this rectangle into two rectangles with integer sides by making a cut parallel to one of the sides of the original rectangle. Then Bob tries to form some other rectangle from the two resulting rectangles, and he can rotate and move these two rectangles as he wishes.
Note that if two rectangles differ only by a $$$90^{\circ}$$$ rotation, they are considered the same. For example, the rectangles $$$6 \times 4$$$ and $$$4 \times 6$$$ are considered the same.
Thus, from the $$$2 \times 6$$$ rectangle, another rectangle can be formed, because it can be cut into two $$$2 \times 3$$$ rectangles, and then these two rectangles can be used to form the $$$4 \times 3$$$ rectangle, which is different from the $$$2 \times 6$$$ rectangle.
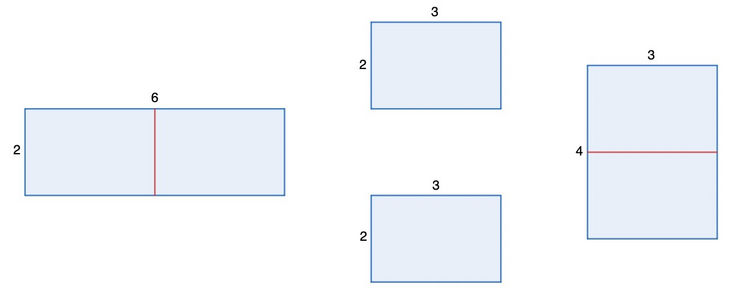
However, from the $$$2 \times 1$$$ rectangle, another rectangle cannot be formed, because it can only be cut into two rectangles of $$$1 \times 1$$$, and from these, only the $$$1 \times 2$$$ and $$$2 \times 1$$$ rectangles can be formed, which are considered the same.
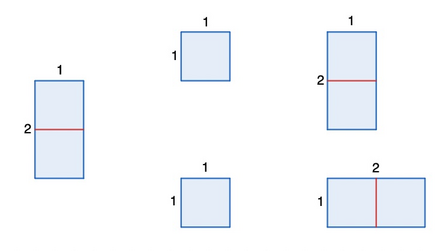
Help Bob determine if he can obtain some other rectangle, or if he is just wasting his time.
Each test consists of multiple test cases. The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — the number of test cases. This is followed by the description of the test cases.
The single line of each test case contains two integers $$$a$$$ and $$$b$$$ ($$$1 \le a, b \le 10^9$$$) — the size of Bob's rectangle.
For each test case, output "Yes" if Bob can obtain another rectangle from the $$$a \times b$$$ rectangle. Otherwise, output "No".
You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive answers.
71 12 12 63 22 22 46 3
No No Yes Yes Yes Yes No
In the first test case, the $$$1 \times 1$$$ rectangle cannot be cut into two rectangles, so another rectangle cannot be obtained from it.
In the fourth test case, the $$$3 \times 2$$$ rectangle can be cut into two $$$3 \times 1$$$ rectangles, and from these, the $$$1 \times 6$$$ rectangle can be formed.
In the fifth test case, the $$$2 \times 2$$$ rectangle can be cut into two $$$1 \times 2$$$ rectangles, and from these, the $$$1 \times 4$$$ rectangle can be formed.
| Name |
|---|




