E. Xenia and String Problem
time limit per test
1 second
memory limit per test
256 megabytes
input
stdin
output
stdout

Xenia the coder went to The Olympiad of Informatics and got a string problem. Unfortunately, Xenia isn't fabulous in string algorithms. Help her solve the problem.

String s is a sequence of characters s1s2... s|s|, where record |s| shows the length of the string.

Substring s[i... j] of string s is string sisi + 1... sj.

String s is a Gray string, if it meets the conditions:

  • the length of string |s| is odd;
  • character 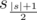occurs exactly once in the string;
  • either |s| = 1, or substrings 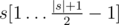and 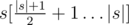are the same and are Gray strings.

For example, strings "abacaba", "xzx", "g" are Gray strings and strings "aaa", "xz", "abaxcbc" are not.

The beauty of string p is the sum of the squares of the lengths of all substrings of string p that are Gray strings. In other words, consider all pairs of values i, j (1 ≤ i ≤ j ≤ |p|). If substring p[i... j] is a Gray string, you should add (j - i + 1)2 to the beauty.

Xenia has got string t consisting of lowercase English letters. She is allowed to replace at most one letter of the string by any other English letter. The task is to get a string of maximum beauty.

Input

The first line contains a non-empty string t (1 ≤ |t| ≤ 105). String t only consists of lowercase English letters.

Output

Print the sought maximum beauty value Xenia can get.

Please do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64d specifier.

Examples
Input
zzz
Output
12
Input
aba
Output
12
Input
abacaba
Output
83
Input
aaaaaa
Output
15
Note

In the first test sample the given string can be transformed into string p = "zbz". Such string contains Gray strings as substrings p[1... 1], p[2... 2], p[3... 3] и p[1... 3]. In total, the beauty of string p gets equal to 12 + 12 + 12 + 32 = 12. You can't obtain a more beautiful string.

In the second test case it is not necessary to perform any operation. The initial string has the maximum possible beauty.