Define the simple skewness of a collection of numbers to be the collection's mean minus its median. You are given a list of n (not necessarily distinct) integers. Find the non-empty subset (with repetition) with the maximum simple skewness.
The mean of a collection is the average of its elements. The median of a collection is its middle element when all of its elements are sorted, or the average of its two middle elements if it has even size.
The first line of the input contains a single integer n (1 ≤ n ≤ 200 000) — the number of elements in the list.
The second line contains n integers xi (0 ≤ xi ≤ 1 000 000) — the ith element of the list.
In the first line, print a single integer k — the size of the subset.
In the second line, print k integers — the elements of the subset in any order.
If there are multiple optimal subsets, print any.
4
1 2 3 12
3
1 2 12
4
1 1 2 2
3
1 1 2
2
1 2
2
1 2
In the first case, the optimal subset is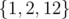 
, which has mean 5, median 2, and simple skewness of 5 - 2 = 3.
In the second case, the optimal subset is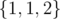 
. Note that repetition is allowed.
In the last case, any subset has the same median and mean, so all have simple skewness of 0.
