| Codeforces Round 366 (Div. 1) |
|---|
| Finished |
Tony Stark is playing a game with his suits (they have auto-pilot now). He lives in Malibu. Malibu has n junctions numbered from 1 to n, connected with n - 1 roads. One can get from a junction to any other junction using these roads (graph of Malibu forms a tree).
Tony has m suits. There's a special plan for each suit. The i-th suit will appear at the moment of time ti in the junction vi, and will move to junction ui using the shortest path between vi and ui with the speed ci roads per second (passing a junctions takes no time), and vanishing immediately when arriving at ui (if it reaches ui in time q, it's available there at moment q, but not in further moments). Also, suits move continuously (for example if vi ≠ ui, at time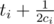 
it's in the middle of a road. Please note that if vi = ui it means the suit will be at junction number vi only at moment ti and then it vanishes.
An explosion happens if at any moment of time two suits share the same exact location (it may be in a junction or somewhere on a road; while appearing, vanishing or moving).
Your task is to tell Tony the moment of the the first explosion (if there will be any).
The first line of the input contains two integers n and m (1 ≤ n, m ≤ 100 000) — the number of junctions and the number of suits respectively.
The next n - 1 lines contain the roads descriptions. Each line contains two integers ai and bi — endpoints of the i-th road (1 ≤ ai, bi ≤ n, ai ≠ bi).
The next m lines contain the suit descriptions. The i-th of them contains four integers ti, ci, vi and ui (0 ≤ ti ≤ 10 000, 1 ≤ ci ≤ 10 000, 1 ≤ vi, ui ≤ n), meaning the i-th suit will appear at moment of time ti at the junction vi and will move to the junction ui with a speed ci roads per second.
If there would be no explosions at all, print -1 in the first and only line of output.
Otherwise print the moment of the first explosion.
Your answer will be considered correct if its relative or absolute error doesn't exceed 10 - 6.
6 4
2 5
6 5
3 6
4 6
4 1
27 6 1 3
9 5 1 6
27 4 3 4
11 29 2 6
27.3
6 4
3 1
4 5
6 4
6 1
2 6
16 4 4 5
13 20 6 2
3 16 4 5
28 5 3 5
-1
