Дано корневое дерево с n вершинами. Король Ночи удаляет ровно одну вершину дерева и все ребра из этой вершины. После этого дерево распадается, и образуется лес деревьев. Вершина, которая удалена, больше не является частью дерева.
Корнем дерева в лесу деревьев является вершина в этом дереве, которая не имеет вершину-родитель. Определим силу леса, как размер самого большого дерева в лесу деревьев.
Джон Сноу хочет минимизировать силу леса дерева. Чтобы сделать это, он может выполнить следующую операцию максимум один раз.
Он удаляет ребро между вершиной и ее родителем и вставляет новое ребро между этой вершиной и любой другой вершиной в лесу, так чтобы количество деревьев в лесу оставалось таким же.
Для каждой вершины v необходимо узнать минимальное значение силы леса, сформированного удалением вершины v.
Первая строка входных данных содержит единственное целое число n (1 ≤ n ≤ 105) — количество вершин в дереве. Каждая из следующих n строк содержит два целых числа ui и vi (1 ≤ ui, vi ≤ n), где ui родитель вершины vi. Если ui = 0, тогда vi корень дерева.
Выведите n строк. i-я строка должна содержать минимальное значение силы леса, сформированного удалением i-й вершины, и применением Джоном Сноу максимум одной операции, описанной выше.
10
0 1
1 2
1 3
1 4
2 5
2 6
3 7
4 8
4 9
5 10
3
4
5
5
5
9
9
9
9
9
2
2 1
0 2
1
1
Дерево в первом тестовом примере изображено ниже.  При удалении первой вершины дерево распадается и формирует следующий лес. Сила этого леса равна 4.
При удалении первой вершины дерево распадается и формирует следующий лес. Сила этого леса равна 4. 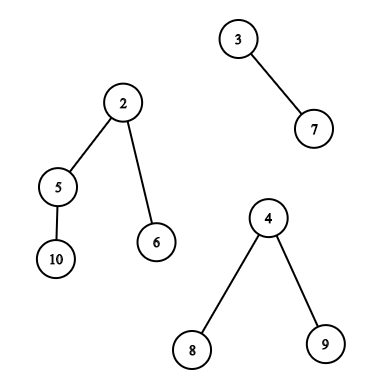 Джон Сноу может поменять родителя вершины 10 с 5 на 3. Сила леса становится равной 3.
Джон Сноу может поменять родителя вершины 10 с 5 на 3. Сила леса становится равной 3. 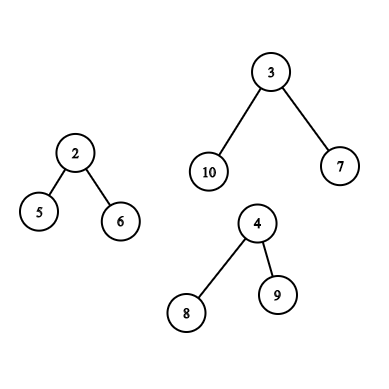
| Название |
|---|




