| Tinkoff Challenge - Elimination Round |
|---|
| Закончено |
Обычный клиент банка Олег решает интересную шахматную задачу: расставить на шахматной доске n × n наибольшее число ладей, чтобы они не били друг друга.
Напомним, что ладья, которая стоит в клетке (a, b), бьет ладью, стоящую в клетке (x, y), тогда и только тогда, когда a = x или b = y.
К сожалению (или радости?) Олега ответ в этой задаче всегда получался равным n, поэтому вскоре задача ему наскучила. Он решил её усложнить, удалив некоторые клетки из шахматной доски. Удалив клетку, Олег подразумевает, что на нее нельзя ставить ладью, однако, бить «сквозь» удаленные клетки ладьи могут.
Олег удаляет клетки группами, а именно, он раз за разом выбирает некоторый прямоугольник по сторонами, параллельными осям координат, и удаляет все клетки в нем. Формально, если он выбрал некоторый прямоугольник, левая нижняя и правая верхняя клетки которого имеют координаты (x1, y1) и (x2, y2), соответственно, то он удаляет все такие клетки (x, y) что x1 ≤ x ≤ x2 и y1 ≤ y ≤ y2. Гарантируется, что никакую клетку два раза Олег удалять не будет, то есть все выбранные прямоугольники не пересекаются.
Эту версию задачи Олег решить не смог, а его друг, к которому он часто обращается за советами, — аналитик Игорь — сейчас очень занят на конференции, и не может помочь Олегу.
Вы — последняя надежда Олега! Помогите ему: по заданному размеру доски и прямоугольникам, клетки в которых удалены, выясните, какое максимальное число ладей можно расставить на доске так, чтобы никакая ладья не била никакую другую.
Первая строка содержит одно целое число n (1 ≤ n ≤ 10000) — размеры доски.
Вторая строка содержит одно целое число q (0 ≤ q ≤ 10000) — количество прямоугольников, которые удалил Олег.
Следующие q строк содержат информацию о прямоугольниках.
В каждой из этих строк содержится четыре целых числа x1, y1, x2 и y2 (1 ≤ x1 ≤ x2 ≤ n, 1 ≤ y1 ≤ y2 ≤ n) — координаты левой нижней и правой верхней клеток прямоугольника, в котором он удаляет клетки.
Гарантируется, что прямоугольники попарно не пересекаются.
В единственной строке выведите максимальное число ладей, которое Олег сможет расставить на поле так, чтобы они не били друг друга.
5
5
1 1 2 1
1 3 1 5
4 1 5 5
2 5 2 5
3 2 3 5
3
8
4
2 2 4 6
1 8 1 8
7 1 8 2
5 4 6 8
8
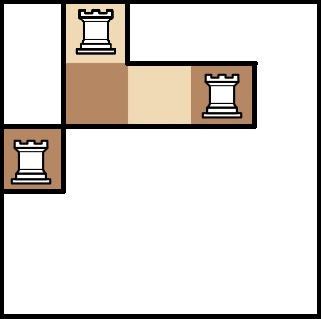
Ниже приведено изображения поля и пример расстановки ладей на нем в первом примере.
| Название |
|---|