Consider an array A with N elements, all being the same integer a.
Define the product transformation as a simultaneous update Ai = Ai·Ai + 1, that is multiplying each element to the element right to it for 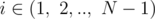 , with the last number AN remaining the same. For example, if we start with an array A with a = 2 and N = 4, then after one product transformation A = [4, 4, 4, 2], and after two product transformations A = [16, 16, 8, 2].
, with the last number AN remaining the same. For example, if we start with an array A with a = 2 and N = 4, then after one product transformation A = [4, 4, 4, 2], and after two product transformations A = [16, 16, 8, 2].
Your simple task is to calculate the array A after M product transformations. Since the numbers can get quite big you should output them modulo Q.
The first and only line of input contains four integers N, M, a, Q (7 ≤ Q ≤ 109 + 123, 2 ≤ a ≤ 106 + 123, 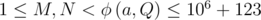 ,
, 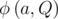 is prime), where
is prime), where 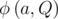 is the multiplicative order of the integer a modulo Q, see notes for definition.
is the multiplicative order of the integer a modulo Q, see notes for definition.
You should output the array A from left to right.
2 2 2 7
1 2
The multiplicative order of a number a modulo Q 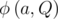 , is the smallest natural number x such that ax mod Q = 1. For example,
, is the smallest natural number x such that ax mod Q = 1. For example, 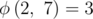 .
.
| Name |
|---|




