You are given a chessboard of size 1 × n. It is guaranteed that n is even. The chessboard is painted like this: "BWBW...BW".
Some cells of the board are occupied by the chess pieces. Each cell contains no more than one chess piece. It is known that the total number of pieces equals to 
.
In one step you can move one of the pieces one cell to the left or to the right. You cannot move pieces beyond the borders of the board. You also cannot move pieces to the cells that are already occupied.
Your task is to place all the pieces in the cells of the same color using the minimum number of moves (all the pieces must occupy only the black cells or only the white cells after all the moves are made).
The first line of the input contains one integer n (2 ≤ n ≤ 100, n is even) — the size of the chessboard.
The second line of the input contains integer numbers 
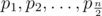(1 ≤ pi ≤ n) — initial positions of the pieces. It is guaranteed that all the positions are distinct.
Print one integer — the minimum number of moves you have to make to place all the pieces in the cells of the same color.
6
1 2 6
2
10
1 2 3 4 5
10
In the first example the only possible strategy is to move the piece at the position 6 to the position 5 and move the piece at the position 2 to the position 3. Notice that if you decide to place the pieces in the white cells the minimum number of moves will be 3.
In the second example the possible strategy is to move 
in 4 moves, then 
in 3 moves, 
in 2 moves and 
in 1 move.
