Problem statement↵
A series of highways connect n cities numbered from 0 to n — 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli.↵
You are also given an integer discounts which represents the number of discounts you have. You can use a discount to travel across the ith highway for a cost of tolli / 2 (integer division). Each discount may only be used once, and you can only use at most one discount per highway.↵
Return the minimum total cost to go from city 0 to city n — 1, or -1 if it is not possible to go from city 0 to city n — 1.↵
↵
**Example 1:**↵
Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], discounts = 1↵
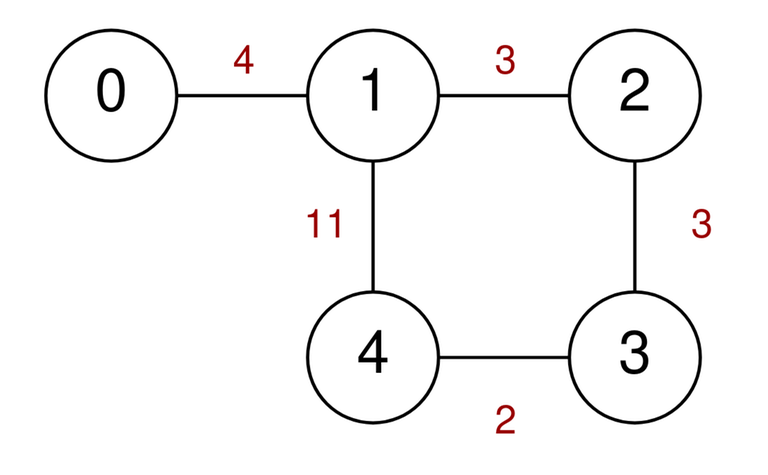↵
Output: 9↵
Explanation:↵
Go from 0 to 1 for a cost of 4.↵
Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5.↵
The minimum cost to go from 0 to 4 is 4 + 5 = 9.↵
↵
↵
**Time complexity**↵
As per my understanding Time complexity for this would be k * E log (V * k). Since Each edge can be reached with k different number of discount values and with decreased toll value everytime (k * E) and also this means each vertex may be present in heap k number of times (log(V * k)). Here K is the number of discounts. Is it correct ?↵
↵
A series of highways connect n cities numbered from 0 to n — 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli.↵
You are also given an integer discounts which represents the number of discounts you have. You can use a discount to travel across the ith highway for a cost of tolli / 2 (integer division). Each discount may only be used once, and you can only use at most one discount per highway.↵
Return the minimum total cost to go from city 0 to city n — 1, or -1 if it is not possible to go from city 0 to city n — 1.↵
↵
**Example 1:**↵
Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], discounts = 1↵
↵
Output: 9↵
Explanation:↵
Go from 0 to 1 for a cost of 4.↵
Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5.↵
The minimum cost to go from 0 to 4 is 4 + 5 = 9.↵
↵
↵
**Time complexity**↵
As per my understanding Time complexity for this would be k * E log (V * k). Since Each edge can be reached with k different number of discount values and with decreased toll value everytime (k * E) and also this means each vertex may be present in heap k number of times (log(V * k)). Here K is the number of discounts. Is it correct ?↵
↵





