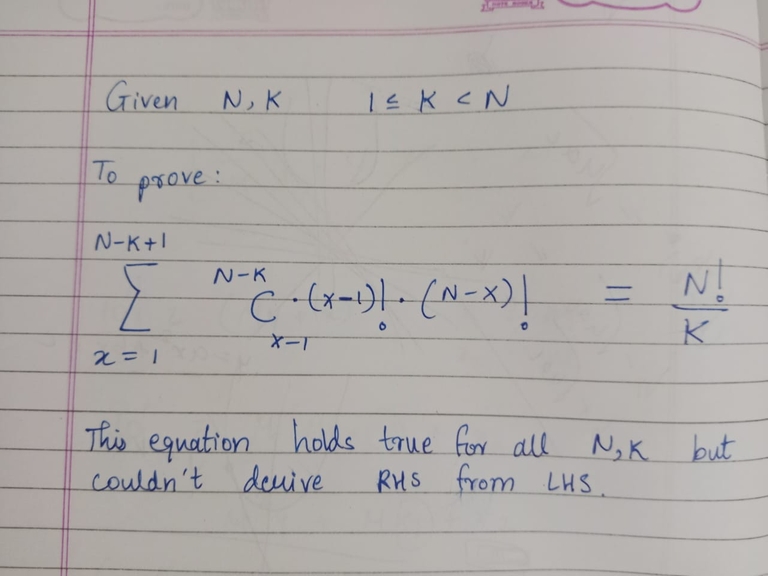• Recently I came across a new idea to solve graph-related problems using segment trees, I would like to discuss the same with a problem.

Problem:

Given a graph $$$G$$$ with $$$N$$$ nodes and many edges (around $$$O(N^2)$$$), Goal is to perform the Dijkstra algorithm on this dense graph and find out the shortest path cost from node 1 to all other nodes.

The edges are given in a compressed format. The input follows $$$M$$$ lines. Each of the $$$M$$$ lines consists of 4 integers U Lx Rx C meaning there are edges from node U to all other nodes in range [Lx , Rx] with cost C. Edges are uni-directional.

Example:

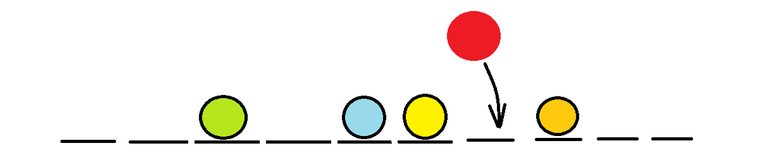
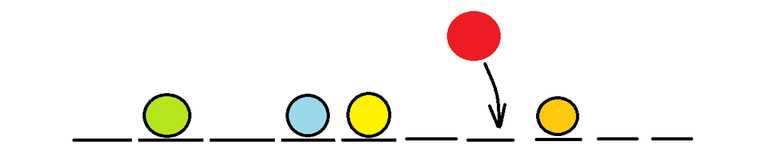
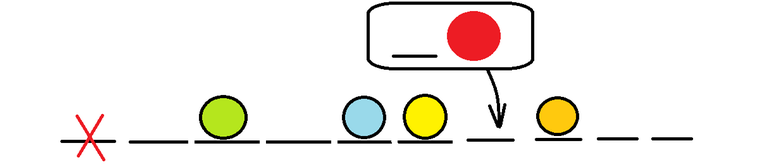
For N = 6 , the edge-group U = 1 , [Lx,Rx] = [3,5] , C = 10 looks like:

Constraints:

• $$$1 \le N \le 10^5$$$
• $$$1 \le M \le 10^5$$$
• $$$1 \le U \le N$$$
• $$$1 \le Lx \le Rx \le N$$$
• $$$1 \le C \le 10^9$$$

Do spend some time thinking about this problem, before proceeding to the solution.

Initial Thought Process:

• The main problem faced here is that in the worst case, we have plenty of edges $$$O(N^2)$$$, performing Dijkstra in this dense graph would lead to time complexity $$$O(N^2 log(N))$$$ which would give TLE. Also, it is not possible to store all edges in the adjacency list, giving MLE.

• So we need to seek out some ways to reduce the number of edges so that time complexity can be improved.

• Our solution proceeds like this, first we try to convert this dense graph to a sparse graph with less number of edges and then perform the Dijkstra Algorithm to find our answer.
• Since the input of edges is also given in compressed format, intuitively we can think that there might be some ways to represent a group of edges as a single edge, so that we can reduce the number of edges and solve our problem.

Solution: Segment Tree as a structure

• One main observation in this problem is that we add edges from node U to a range of nodes [Lx, Rx]. This gives an intuition that we deal with ranges and we can use segment trees to solve our problem.
• In our solution, We only use the structure and ideas of segment tree (complete binary tree). We dont calculate or store anything in the segment tree nodes.
• First, we build a segment tree $$$G'$$$ with $$$N$$$ leaf nodes, ($$$2N$$$ nodes in total). These $$$N$$$ leaf nodes represent the $$$N$$$ nodes of the original graph $$$G$$$ and add edges from parent to its left and right children with 0 cost.

Example N = 8

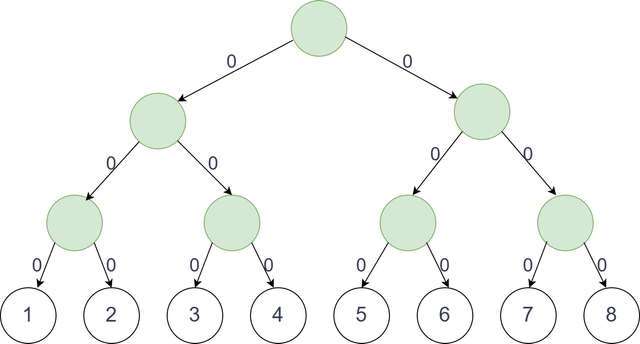
• It is a well known fact that any range [Lx , Rx] can be covered by $$$O(log(N))$$$ nodes in a segment tree. So for every edge-group U Lx Rx C, we add edges from node U to these $$$O(log(N))$$$ nodes with cost C.

Example: N = 8, U = 1, [Lx,Rx] = [3,8], C = 10

• Since from any intermediate node, we can visit the leaf nodes in its subtree with 0 cost, this graph $$$G'$$$ preserves the same information of graph $$$G$$$.
• Total number of edges is $$$2N$$$ (intial graph) + $$$M*logN$$$ (for each edge-group), So total edges are $$$E = O(Mlog(N))$$$.
• Performing dijkstra in this graph $$$G'$$$ would give time complexity $$$O(Mlog^2(N))$$$ which would pass under the given constraints.

Problems using this idea:

• Problem 1

• Problem 2

Problem D2: Line of Delivery (Part 2) Link

Hello everyone, I'd like to talk about Problem D2 from the recent Meta Hacker Cup 2024 Practice Round. The solution suggests that we can use a treap data structure to efficiently handle the operations described in the problem.

Operation 1) Insert a stone at $$$E_i^{th}$$$ empty position.
Operation 2) Move all stones to the left of the inserted stone by 1 unit in the negative direction.

Yes, treaps can be used to solve this problem, but I’ve come up with a simpler solution using a vector approach. Let's maintain an array called emptyPlaces that stores information about all the empty spots. In this array, I track how many balls are located immediately to the right of each empty position. So emptyPlaces[i] denoted how many consecutive balls are immediately right towards $$$i^{th}$$$ empty slot. Additionally, I keep a start pointer to mark the current starting position in the array.

So the above 2 operations can be modified as follows:

Operation 1) emptyPlaces[start + Ei - 1]++; (0-based indexing)
Operation 2) start++; Just moving the start pointer can handle the shifting case mentioned in operation 2) above.

The key advantage of this approach is that we shift the stones to the left of the newly inserted stone by 1 unit in the negative direction. This can be visualized as adding an empty spot to the left of the inserted stone and removing the first empty position from the array.

Example:

Here in this case, the emptyPlaces array looks like $$$[0,1,2,1,0,0]$$$

Let's say a ball is thrown with $$$E = 4$$$, then the $$$4^{th}$$$ empty position is occupied by this new red ball.

Now Since this new ball has collided with the previous 3 balls at position 3,5,6 then these balls move 1 unit towards left.

This can be visualized like adding a new empty slot on left of new ball, and deleting an empty slot at the start of the track.

Now if we notice the emptyPlaces array, it changes to $$$[1,2,2,0,0]$$$. After adding the empty slot and new ball combined to $$$4^{th}$$$ position, the emptyPlaces array changes to $$$[0,1,2,2,0,0]$$$. Since the previuos balls move 1 unit left, we can delete the first element in emptyPlaces array and it changes to $$$[1,2,2,0,0]$$$.

Just maintaining these could get me all the distinct positions of the final balls, and since the thrown balls are in order toward the negative x direction, finding the position of each ball is relatively easy.

// #pragma GCC optimize("Ofast")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,fma")
// #pragma GCC optimize("unroll-loops")
		
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef long double ld;
typedef vector<int> vi;
typedef vector<ld> vld;
typedef vector<pair<ll , ll>> vpll;
typedef vector<pair<ld , ld>> vplld;
typedef pair<int,int> pii;
typedef vector<pair<int,int>> vpii;
typedef vector<ll> vl;
typedef pair<ll,ll> pll;
typedef priority_queue<ll> pq;
typedef priority_queue<pair<ll,ll>> pqp;

#define fi first
#define se second
#define pb push_back
#define mp make_pair

#define print(a) for(auto x:a) cout<<x<<" ";cout<<endl;
#define printarr(a , n) for(int i = 0 ; i < n  ;i ++) cout << a[i] << " "; cout << endl;
#define endl '\n'
#define sq(a) (a)*(a)
#define yes  cout << "YES" << endl;
#define no  cout << "NO" << endl;


int emptyPlaces[2000005] = {0};

void solve()
{
	ll n , k;
	cin >> n >> k;

	vl a(n);
	for(int i =  0 ; i < n ; i ++)
	{
		cin >> a[i];
	}

	// clear all empty information
	for(int i = 0 ; i < 2000005 ; i ++)
	{
		emptyPlaces[i] = 0;
	}

	int start = 0;

	for(int i = 0 ;i  < n ; i ++)
	{
		emptyPlaces[start + a[i] - 1]++;
		start++;
	}

	int position = 1;
	vl ballPosition;

	for(int x = start ; x < 2000005 ; x ++)
	{
		position++;  // currently I have a empty slot
		for(int guys = 0 ; guys < emptyPlaces[x] ; guys++)
		{
                        // balls occupied to the right of this empty slot
			ballPosition.pb(position++);
		}
	}	

	reverse(ballPosition.begin() , ballPosition.end());

	pll ans = {inf , inf};

	for(int i = 0 ;i  < n ; i ++)
	{
		ans = min(ans , {abs(ballPosition[i]-k) , i+1});
	}
	cout << ans.second << " " << ans.first << endl;
}

int main(){

	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	

	#ifndef ONLINE_JUDGE
		freopen("line_of_delivery_part_2_input.txt", "r" , stdin);
		freopen("output.txt", "w" , stdout);
	#endif

	int t=1;
	cin>>t;

	for(int i = 1 ; i <= t ; i ++)
	{
		cout <<"Case #"<<i<<": ";
    	solve();
	}	
	return 0;
}

Let $$$C_i$$$ be $$$i^{th}$$$ catalan number. Is it possible to derive a generalised formula for convolution of catalan numbers in $$$k$$$ variables.
For example:

For $$$K = 2$$$,
$$$\sum_{i=0}^{n} {C_iC_{n-i}} = C_{n+1}$$$

For $$$K = 3$$$,
$$$\sum_{i=0}^{n} \sum_{j=0}^{n} {C_iC_jC_{n-i-j}} = C_{n+2} - C_{n+1}$$$

For $$$K = 4$$$,
$$$\sum_{i=0}^{n} \sum_{j=0}^{n} \sum_{k=0}^{n} {C_iC_jC_kC_{n-i-j-k}} = C_{n+3} - {2 C_{n+2}}$$$

I wanted to know, does any formula exist for any generalized K?

Hello everyone,

I did like to give a brief overview of Fermat's theorem and its proof. There are various methods to prove Fermat's Little theorem, but I found the combinatorial approach to be the most straightforward and easy to understand. I'd like to discuss Fermat's theorem and its proof using combinatorics.

Fermat's Little Theorem

It states that if $$$p$$$ is a prime and $$$a$$$ is any integer not divisible by $$$p$$$, then $$$a^{p−1} − 1$$$ is divisible by $$$p$$$

Example:

Say a = 2 , p = 5.
$$$a^{p-1} $$$
$$$ = 2^{5-1}$$$
$$$ = 2^4 = 16$$$
$$$ \equiv 1 \pmod{5}$$$

Proof (Combinatorics Approach)

The concept behind this proof is to approach it through a combinatorial problem and discover its solution, which indirectly verifies the theorem. Let's explore this straightforward combinatorial problem.

Problem

Consider a Necklace chain consisting of beads. There are $$$p$$$ beads in this chain. You are allowed to color each bead with $$$a$$$ possible colors available. The colors are available in infinite amounts, there is no other restriction on coloring. Find the number of ways to color these beads.

It can be easily shown that there are $$$a^p$$$ ways to color the beads to get different necklaces. (considering cyclic rotations as distinct). Every bead has $$$a$$$ options to be colored.

Consider a small variation to this problem, Among all possible $$$a^p$$$ permutations, Let's try to group them based on similar cyclic rotations. Two permutations are said to be equivalent if any of them can be generated from the cyclic rotation of the other.

For example, consider $$$a = 2, p = 3$$$. Let X and Y be the 2 possible colors available. Let's try to group these $$$2^3 = 8$$$ strings (all permutations) based on similar cyclic rotations. We get:

• Group 1: XXX
• Group 2: YYY
• Group 3: XXY, XYX, YXX
• Group 4: XYY, YYX, YXY

Here we get 4 different groups of sizes 1,1,3,3 each. Let's try to analyze these group sizes in-depth.

Periodicity of a String:

The periodicity of a string refers to the smallest length of a substring that, when repeated, forms the entire string. In other words, it's the minimum length of a substring that can be repeated periodically to recreate the original string.

Example

• ABCABC has periodicity = 3 (ABC)
• ABABAB has periodicity = 2 (AB)

Claim 1

The periodicity of a string is the same as its group size of similar cyclic rotations.

Claim 2

The periodicity of a string, as well as its group size, are factors of the string's total length.

From the above 2 claims, we can conclude that for the original problem (filling $$$p$$$ beads with $$$a$$$ colors) we get $$$a^p$$$ strings, and these strings have periodicity as $$$1$$$ or $$$p$$$. ($$$1$$$ and $$$p$$$ are the only factors of $$$p$$$ (prime)).

Example $$$a = 2, p = 3$$$

• Group 1: XXX Periodicity = 1
• Group 2: YYY Periodicity = 1
• Group 3: XXY, XYX, YXX Periodicity = 3
• Group 4: XYY, YYX, YXY Periodicity = 3

It can also be shown that among $$$a^p$$$ strings, there are only $$$a$$$ strings with periodicity as $$$1$$$. (Same color applied to all beads Example: Group 1: XXX, Group 2: YYY)

From the above statements we can conclude that the remaining strings $$$a^p - a$$$ have periodicity as $$$p$$$, which says that we can separate the remaining $$$a^p - a$$$ strings into groups of sizes $$$p$$$. This concludes that $$$a^p - a$$$ is a multiple of $$$p$$$. So

$$$a^p - a \equiv 0 \pmod{p}$$$
$$$a^p \equiv a \pmod{p}$$$
$$$a^{-1}*a^p \equiv a^{-1}*a \pmod{p}$$$
$$$a^{p-1} \equiv 1 \pmod{p}$$$

This completes the proof. My main motivation for exploring such proofs is the belief that visualizing a problem from different perspectives can simplify the process, making the proofs more intuitive and accessible, rather than relying solely on rigorous mathematical approaches.

References:

1) Wikepedia

I came across an equation, but I am not able to prove it. Can somebody help me proving this equation.

Problem Link

Is it possible to calculate the following recurrences in $$$O(N*2^N)$$$.

1) $$$dp[mask] = min(dp[mask] , dp[m_1] + dp[m_2]);$$$
where $$$m_1|m_2 = mask$$$

2) $$$dp[mask] = min(dp[mask] , dp[m_1] + dp[m_2]);$$$
where $$$m_1 \oplus m_2 = mask$$$ and $$$m_1$$$ ,$$$m_2$$$ are subsets of mask.

Hello, Codeforces!

We are glad to invite you to participate in a reverse coding challenge hosted by technical fest Pragyan, NIT Trichy, which will take place on Friday, 23rd February, from 5:00 PM to 7:00 PM IST.

Pragyan, in association with Spider, presents Decode It. A reverse coding and logical reasoning contest on Hackerrank will go live on 23rd February, from 5:00 PM to 7:00 PM. A 120-minute contest to test your logical reasoning and coding abilities.

Think you have what it takes to reach the top? Test your logical and coding skills in a beginner-friendly contest.

CASH PRIZES Distribution (Indian Participants):

• Prize pool : INR 10000.
• Top 3 performers will be awarded cash prizes of INR 5000, 3000, and 2000, respectively.

Contest Date: Friday, 23rd February
Contest Timing: 17:00 to 19:00 IST
Registration Link:Link
Discord link: Link
Pragyan Website link: Link
Duration: 120 minutes

Only Indian college students and registered participants will be eligible for prizes. Please join the discord server for getting regular updates about the event.

We want to thank:

• Problem Setter: ASHWANTH_K, -CODER001
• Problem Tester: ASHWANTH_K, -CODER001
• Development Team: Nanthana2003
• We would also like to thank Don_Wick , rkviswakrishnan for timely help in generating and testing executable files.
• Special mentions to Nikolai_Tesla for giving good ideas about the event.
• Spider (Technical club of NIT Trichy) for providing all required resources and moral support.
  Hackerrank for supporting the event, their invaluable help, and their excellent platform.

Solutions for all the questions will be posted shortly after the contest ends!

https://cses.fi/problemset/task/2174
i am clueless for this problem. please help me .
I have solved the easy verison of problem using O(N) dp.
I have spent a good amount of time thinking but could not find any solution.

It would be nice if i get any hints.. instead of actual solution...

I have given thoughts about matrix exponentiation, or any observation patterns ... nothing seems to workout.

• Problem Link: https://cses.fi/problemset/task/2402
• I have solved this problem using component merging ideas. complexity: $$$O(Nlog^2(N))$$$
• Numbers belonging to the same component are assigned in the same stack.
• One observation I could see was, that if I am able to do an output operation, it's always optimal to output the number as early, without delaying the output operation.
• Another observation, we could maintain currently active numbers, and if any new number $$$X$$$ is added, we could make a component for all numbers < $$$X$$$
• I felt happy to solve this problem on my own, as it had only 73 correct submissions till now.
• I am curious to know if there exists a simpler approach (any mind-blowing observation/ lower complexity) to solve this.

https://codeforces.net/contest/1721/submission/218867337
In this submission, for 4th testcase i get TLE. But 4th testcase participant output is printed, Why is it so...

I will account for good observations and ideas while solving problems in codeforces/CodeChef/atcoder . The proofs of the below statements will not be mentioned here; It's advised to do such proofs on your own for exercise.

• Lets say I have a set $$$S$$$ consisting of integers, denote its $$$lcm(S) = L$$$, I add a new element $$$x$$$ to this set $$$S$$$ , Lets deonte the new set as $$$S'$$$,where $$$S' = union(S , x)$$$ and its $$$lcm(S') = L'$$$. Can we deduce a relation between $$$L$$$ and $$$L'$$$? We can observe $$$L = L'$$$ or $$$L' >= 2*L$$$.
  

  ---

• We want to find two numbers in an array $$$A[]$$$ with maximum common prefix bits in binary representation. It's easy to show that those two numbers always occur as adjacent numbers in $$$sorted(A[])$$$

  ---

• The number of distinct gcd prefixed/suffixed at an index in an array will never exceed $$$log(A_{max})$$$
  

  ---

• Let's say I have a number $$$X$$$, And I apply modulo operation as many times as I wish, i.e $$$X = X \% {m_i}$$$ for some different values of $$${m_i}$$$. It can be shown that $$$X$$$ takes $$$log(X)$$$ distinct values until it reaches to $$$0$$$.
  

  ---

• If $$$N$$$ times $$$abs()$$$ function appears at any problem, maybe bruteforcing all $$$2^N$$$ combinations of $$$+/-$$$ may give way to the solution sometimes. Especially when we need to compute a function of form $$$max(abs(...))$$$
  

  ---

• Prefix Bitwise Or/And can take a maximum of $$$log(max(A[i]))$$$ values.

  ---

• Nested totient function say $$$phi(phi(phi( ... (X) ... )))$$$ will eventually reach 1 in atmost $$$2log(X)$$$ nested functions. Useful for computing expressions like $$$(A^{(B^{(C^..)})})$$$ modulo $$$P$$$. (nested powers).

  ---

• SOS dp may help to compute the number of $$$i$$$ such that $$$A[i]$$$ is a subset/superset/no bits common to a given mask $$$X$$$

  ---

• Partial optimisation of SOS dp leading to $$$3^N$$$ complexity may pass for $$$N <=15$$$.

  ---

• Whenever You want to maximize/minimize bitwise properties among some elements, consider iterating from the last bit and checking its possibility. This greedy assigning from the last bit will work.
  

  ---

• Any counting problem, like counting pairs of elements/counting subarrays satisfying some property: If any common technique, like fixing the L pointer or 2pointer approach, does not work, try to divide and conquer. It may be easy to come up with a solution sometimes. https://codeforces.net/contest/1849/problem/E

  ---

• The contribution Technique impresses me every time. Try this: https://atcoder.jp/contests/abc312/tasks/abc312_g. Hint: number of ways of choosing three nodes in the same tree path can be converted to summating all path lengths in the tree.
  

  ---

• General Technique: For counting problems: try to fix some parameters and iterate on it. It may happen that fixing just one parameter may be difficult sometimes to count properly. So try to do casework and identify which cases can be easily calculated by fixing different parameters. Eg, let's say my problem can be divided into 2 cases, $$$case1$$$ and $$$case2$$$. It can happen that fixing parameter $$$A$$$ can be easy to count distinct answers for $$$case1$$$, and fixing another parameter $$$B$$$ can be easy to count distinct answers for $$$case2$$$. Try this: https://codeforces.net/contest/50/problem/E Hint: case1: rational, case2: irrational roots.
  

  ---

• It's not wrong to complicate ur solution with a lazy segtree. Try this: https://codeforces.net/contest/1553/problem/F

  ---

• Lets take an array $$$A$$$ and let $$$f(x)$$$ be number of subsequence with $$$Xor(subseq) = x$$$. It can be shown that $$$f(x)$$$ is always a power of 2. Strong result: f(x) = 0 or f(x) = f(x1) = f(x2) ...!= 0. More insights on this can be understood well by studying the xor basis technique.
  

  ---

• $$$O(N^2)$$$ may give tle, but $$$O(N^2/64)$$$ will pass. clue: BITSETS

  ---

• Maximum Manhattan distance between 2 points: convert every point $$$(x,y)$$$ to $$$(x',y') = (x-y,x+y)$$$. then $$$answer = max(max(x')-min(x') , max(y')-min(y')) $$$

  ---

• If you find some observation or pattern problem, better bruteforce all possibilities to arrive at observing patterns quicker. https://codeforces.net/problemset/problem/1730/D, I tried brute-forcing all possibilities; it happened that I could figure out some common pattern everywhere, then I proceeded to put claims, and it happened that they were true.
  

  ---

• Any array operation, like adding on an interval, adding $$$+x$$$ on some subsequence of the array, or any other variation, try to think its effect of operations on the prefix sum. This may give a clue to the answer. Eg, https://codeforces.net/contest/1556/problem/E
  

  ---

• https://codeforces.net/problemset/problem/623/B If I remove a subarray of size < N from an array, then either the first element or the last element remains as it is...
  

  ---

• $$$gcd(x,y) = gcd(x-y,y) = gcd(x,y-x)$$$ https://leetcode.com/contest/biweekly-contest-96/problems/check-if-point-is-reachable/

  ---

• Idea: Intuitive Proof of Dijkstra problem. Consider a graph problem where I have to find the shortest distance from source to destination where all edges are undirected and weighted. Additional constraint, all costs of edges $$$ c_i = W $$$ where W is a positive integer. This modified problem with all equal weights can be solved with simple BFS.

• Now consider the real problem of Dijkstra, where I have varying edge weights. I can add dummy nodes at the intermediate of those edges to make all edge weights equal. Example: If $$$w_i$$$ is the weight of the edge between $$$u$$$ and $$$v$$$.

• Then I can add $$$w_i-1$$$ dummy nodes equidistant from $$$u$$$ and $$$v$$$ to make all edges cost $$$1$$$. Now, our problem has a BFS solution with complexity $$$sum(w_i)$$$. But I am concerned only with the original nodes' distance values in the graph.
• I need not calculate my dummy node's distance. So we can fast-forward this BFS to calculate the distance of only the original nodes. This fast-forwarded version of BFS is simply DIJKSTRA.
  

  ---

• Lets say I want to factorize $$$N$$$ , precompute all primes from 1 to $$$sqrt(N)$$$ and check for each prime. Complexity = $$$O(sqrt(N)/log(sqrt(N)))$$$ which is just $$$3500$$$ for $$$10^9$$$
  

  ---

• Lets say U want to compute shortest distances on a graph with many edges (n^2) this would give tle ... but we could seek out some way to reduce the count of edges. lets say node u is conneted to all nodes (L...R) , then we can represent a segtree of these nodes and add edge from node u to only logn intervals. (L...R) can be covered by atmost 2logN intervals . So we can add edge from u to these intervals. Also we can edges from every node to its children in segtree with 0 cost. Running dijkstra on this segtree would solve the problem. https://codeforces.net/contest/786/problem/B practice problem.
  

  ---

• Inclusion exclusion on masks: it's just enough to change + to — in SOS DP, everything is taken care.
  

  ---

I dont know what to put here.... Pls help

Hello Codeforces!

We are glad to invite you to participate in a contest hosted by technical fest Pragyan, NIT Trichy, which will take place on Thursday, 23rd March, from 5:30 PM to 7.10PM IST.

Pragyan, in association with Spider, presents Code Venture. An competitive programming contest on Codechef which will go live on 23rd March from 5:30-7:10 pm. An 100 minute contest to test your problem solving and thinking abilities.

Think you have what it takes to reach the top? Test your programming skills in a beginner friendly contest.

The contest is unrated for everybody and common for all divisions.

CASH PRIZES Distribution (Indian Participants):

• Top 3 performers will be awarded cash prizes of INR 15000, 9000, and 6000, respectively.

Contest Link: CDVN23
Contest Date: Thursday, 23rd March
Contest Timing: 17:30 to 19:10 IST
Registration Link:Link
Google form link: Link
Duration: 100 minutes

Only registered participants will be eligible for prizes.

We want to thank:

Problem Setters

• rxhxn_30,aadarsh_ram,amitkumar2003.edu,ASHWANTH_K,ayushkumarsandil,vvipulpatel,sobhagyaSD

Problem Testers

• narendra_chiku,ayushkumarsandil,shubham_up_47,GR_Bhau,vvipulpatel,vivek_yamsani,sobhagyaSD,e_n_i_g_m_a,Genichiro,lazarus249,mds_108,rebelz123

CodeChef for supporting the event, their invaluable help, and their excellent platform.

Editorials for all the questions will be posted shortly after the contest ends!