161A - Оденьте их скорее!
Будем рассматривать бойцов в порядке сортировки, то есть так как они заданы во входных данных. Утверждается, что для текущего бойца всегда выгодно из всех неиспользованных подходящих бронежилетов выбирать тот, у которого bj минимально.
В таком случае задача решается используя метод <<двух указателей>>. Первый указатель двигается по бойцам. Вторым указателем подбирается минимальный по размеру бронежилет из неиспользованных такой, что bj - x ≥ ai.
Асимптотическая сложность решения O(n + m).
Автор идеи: Burunduk1
161B - Скидки
Задача решается жадным алгоритмом. Пусть у нас есть x табуреток. Можно доказать, что всегда выгодно min(k - 1, x) максимальных табуреток разложить в min(k - 1, x) корзинок по одной.
Все оставшиеся табуретки и карандаши нужно положить в оставшиеся пустые корзинки. Заметим, что либо у нас не останется табуреток, либо останется ровно одна пустая корзинка.
Авторы идеи: Burunduk2 и Burunduk1
161C - Абракадабра
Предположим, что максимальный по значению символ в строке входит в ответ. Тогда ответ равен min(r1, r2) - max(l1, l2). Предположим, что это не так. Тогда нужно разрезать каждую из строк по этому символу (в одной из частей может получиться пустая строка) и запустить алгоритм рекурсивно от каждой из полученных пар строк. Можно доказать, что это решение имеет сложность O(K), где K — значение максимального символа.
Другое решение:
Задача решается перебором старшего (то есть, наиболее редкого) символа, который будет находиться в наибольшей общей строке. То есть, если x — старший символ, который встречайтся в обоих строках, и (это важно) в строках не встречаются более редкие символы, то ответ считает по несложной формуле. Второе условие (в строках не встречаются символы, более редкие, чем рассматриваемый) может, вообще говоря, не выполняться. Но его легко достичь, заменив строки на списки строк: если сейчас рассматривается символ x, то вместо каждой из строк у нас будет по несколько строк: изначальные строки, разбитые символами, которые старше x. Причём в каждом списке имеет смысл хранить не более двух строк: если более редкие символы разбивают на три и более подстроки, то среди этих подстрок встретятся «полные» строки. Например, если строку badabaca разбить по символам не младше c, получится список ba, aba, a. Очевидно, что из этих трёх строк достаточно оставить одну aba. Осталось научиться дробить строки и считать ответ для фиксированного старшего символа. Для этого рассмотрим, как зависит символ от позиции в строке.
Здесь удобно нумеровать символы строки с единицы, тогда:
- на нечётных позициях стоят символы «a»
- на чётных позициях стоят символы «b» и старше
- на позициях, кратных четырём, стоят «c» и старше
- на позициях, кратных восьми, стоят «d» и старше
- и так далее, символ соответствует степени двойки, входящей в номер позиции
Используя эту закономерность, можно проверять, лежит ли в строке символ x или старше, и находить его позицию. Для этого достаточно найти минимальную степень двойки, не меньшую левой границы строки. Если она не выходит за правую границу, это и будет ответ.
В итоге решение может быть следующим:
- Перебираем символы, начиная со старшего. На каждом шаге храним два списка: подробленную первую подстроку и подробленную вторую. Изначально эти списки содержат по одному элементу, собственно, исходные строки.
- На каждом шаге перебираем пары строк из имеющихся списков и проверяем,лежит ли текущий символ в каждой из выбранных подстрок. Если лежит — обновляем ответ.
- Перед тем, как перейти к следующему (то есть, более младшему) символу, переразбиваем списки строк. Если в каком-то списке окажется хотя бы три строки, то из них можно оставить вторую (она гарантированно будет полной строкой соответствующего уровня).
Автор идеи: avm
161D - Расстояние в дереве
Эту задачу можно было решать методом динамического программирования. Подвесим дерево за какую-нибудь вершину. Для каждой вершины v дерева, посчитаем значания d[v][lev] (0 ≤ lev ≤ k) — количество вершин в поддереве, расстояние до которых равно lev. Заметим, что d[v][0] = 0.
Далее по этим значениям посчитаем ответ. Ответ равен, сумме по всем вершинам v двух величин:
- Количество путей длины k, которые начинаются где-то в поддереве вершины и заканчиваются в самой вершине. Это количество очевидно равно d[v][k].
- Количество путей длины k, которые начинаются где-то в поддереве вершины и заканчиваются в где-то в поддереве вершины. Это количество равно сумме по всем сыновьям u вершины v величины
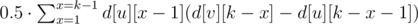 .
.
Считаем сумму по всем вершинам. Получаем решение за O(n·k).
Автор идеи: Burunduk1
161E - Медвежатник Поликарп
Необходимо посчитать количество симметричных матриц с заданной первой строкой, каждая строка которой представляет собой простое число.
Так как матрица симметричная, то она полностью определяется своими элементами не ниже главной диагонали. Переберём все возможные значения цифр, которые находятся в клетках выше главной диагонали (не более 106 вариантов). Заметим, что теперь значения оставшихся неопределёнными цифр, которые стоят на главной диагонали, независимы между собой, так как каждое из них влияет ровно на одну строку матрицы. Поэтому достаточно независимо посчитать количество возможных вариантов для каждой из цифр на диагонали и перемножить полученные значения, чтобы получить количество способов дополнить матрицу до требуемой.
Более того это количество можно предподсчитать заранее для каждой неизвестной позиции и для каждого набора уже известных цифр. Такое решение уже укладывается в ограничение по времени.
Можно было пойти и дальше, отсекаясь при переборе значений цифр выше главной диагонали, если после добавления очередной цифры её строку или столбец больше нельзя было дополнить до простого числа (возможность это сделать так же можно предподсчитать заранее). Данное решение позволяет найти ответы для всех возможных тестов за отведённое время, но это не требовалось.
Автор идеи: avm
Задачи раунда готовили (в алфавитном порядке): arseny30, at1, avm, Burunduk1, Burunduk2, burunduk3, Gerald, levlam, MikeMirzayanov, Nickolas, vysheng










