This is the problem. This is my WA attempt.
What I have observed is that a maximum of (n/2-1) maxima is possible for an array of size n, where n is even. So initially I created another array q such that the final array a = p+q , has all elements equal. Then I greedily tried to create (n/2-1) maximas by swapping the elements of array q( In the code it's ans array). I am willing to explain more if clarification is needed. Please just give me the hint, I want to solve it myself.
I will be thankful for any help!











 But, I think my answer which is 4 for this case is correct. Let me explain this, Starting from the beginning of sorted array l, suppose that everyone who says that the number of liars is less than or equal number of people left after excluding the person who says this and excluding the people who are truth speakers must be telling the truth.
But, I think my answer which is 4 for this case is correct. Let me explain this, Starting from the beginning of sorted array l, suppose that everyone who says that the number of liars is less than or equal number of people left after excluding the person who says this and excluding the people who are truth speakers must be telling the truth.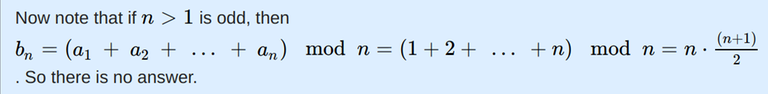 The tutorial says that for n>1 and n is odd, there exists no solution because, b_n = (a_1 + a_2 + ... + a_n)%n = (1+2+3+....+n)%n = (n*(n+1)/2)%n = 0 and b_1 is already 0, and there can't be two zeros in the array b. Hence, no solution for n>1 and n is odd.
The tutorial says that for n>1 and n is odd, there exists no solution because, b_n = (a_1 + a_2 + ... + a_n)%n = (1+2+3+....+n)%n = (n*(n+1)/2)%n = 0 and b_1 is already 0, and there can't be two zeros in the array b. Hence, no solution for n>1 and n is odd. 
