Всем привет.
Недавно мне посчастливилось подготовить задачу про цифровой корень на Russian Code Cup. В результате прорешивания, а также комментариев к разбору, я заметил, что, к сожалению, отнюдь не каждый осведомлен о свойствах данной функции. Я просто не мог остаться равнодушным к этой проблеме.
Для начала рассмотрим определение цифрового корня, взятое с англоязычной Википедии с моим переводом:
Цифровой корень натурального числа — это цифра, полученная в результате итеративного процесса суммирования цифр, на каждой итерации которого для подсчета суммы цифр берут результат, полученный на предыдущей итерации. Этот процесс повторяется до тех пор, пока не будет получена одна цифра.
Например цифровой корень 65,536 это 7, потому что 6 + 5 + 5 + 3 + 6 = 25 и 2 + 5 = 7.
Для начала заметим очевидное свойство (dr(n) — цифровой корень числа n):
Дальше докажем следующий факт: Сумма цифр числа n имеет такой же остаток при делении на 9, как и число n.
В доказательстве нам понадобится формула 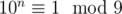 , докажем ее по индукции:
, докажем ее по индукции:
База: 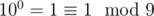
Переход: 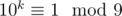 .
.
Нужно доказать 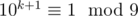 . Просто распишем
. Просто распишем 
Таким образом мы доказали по индукции, что 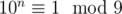 .
.
Вернемся к основному доказательству. Пусть 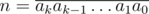 , тогда: n = ak·10k + ak - 1·10k - 1 + ... a1·10 + a0. По только что доказанной формуле:
, тогда: n = ak·10k + ak - 1·10k - 1 + ... a1·10 + a0. По только что доказанной формуле: 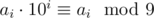 следовательно
следовательно 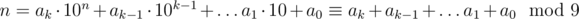 . Что и требовалось доказать.
. Что и требовалось доказать.
Теперь по только что доказанному утверждению понятно, что остаток при делении на 9 — инвариант относительно взятия цифрового корня, а поскольку сумма цифр числа меньше самого числа, если число больше 9, справедливы следующие две формулы:
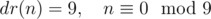
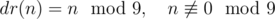
Эти две формулы можно собрать объединить формулой:
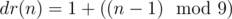
Из этой формулы, например, следует периодичность цифрового корня.
Любая задача про цифровой корень становится легче при знании этого несложного факта, надеюсь, что кому-нибудь этот пост покажется полезным.
Поддержано грантом для одаренной молодежи А. А. Шалыто.









