Because 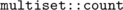 works in O(n) time.
works in O(n) time.
Quite recently I needed to solve this kind of problem:
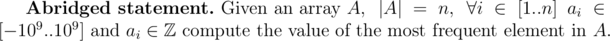
I decided to use 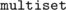 , since it had some useful method called
, since it had some useful method called  . And since I needed to count the elements I coded something like this:
. And since I needed to count the elements I coded something like this:
int main() {
int n;
vector<int> a(n);
multiset<int> cnt;
/* Read array */
// Insert elements in multiset
for (auto i : a)
cnt.insert(i);
// Choose among all elements of a the most frequent
int ans = 0;
for (auto &i : cnt)
ans = max(ans, cnt.count(i));
cout << ans << endl;
return 0;
}
Now. The problem was that this code was judged TLE for, seemingly, no reason at all! Having lost thirty minutes trying to understand where my complexity analysis skills failed, in desperation, I replaced multiset with an ordinary 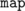 :
:
int main() {
int n;
vector<int> a(n);
map<int, int> cnt;
/* Read array */
// Insert elements in multiset
for (auto i : a)
cnt[i]++;
// Choose among all elements of a the most frequent
int ans = 0;
for (auto &i : cnt)
ans = max(ans, cnt[i]);
cout << ans << endl;
return 0;
}
and it passed! But I was still a bit salty, so I tried to figure out why did this happen: clearly there is something wrong with multiset.
First of all, insertion and searching in 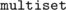 and
and 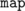 is the same
is the same 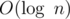 since they both internally implemented as Red-Black trees. The only thing that is nor the first nor the second is the
since they both internally implemented as Red-Black trees. The only thing that is nor the first nor the second is the  method in the first snippet. So, this must be the reason why the code failed.
method in the first snippet. So, this must be the reason why the code failed.
At that point, I've dived into the source code of the 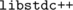 . The headers for it on Unix machine should be located at
. The headers for it on Unix machine should be located at  , where
, where  is the version of the compiler (run
is the version of the compiler (run 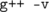 to get it). There we can see
to get it). There we can see 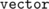 ,
, 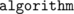 and
and  files among many.
files among many.  yields
yields
// Licence is omitted
/** @file include/set
* This is a Standard C++ Library header.
*/
#ifndef _GLIBCXX_SET
#define _GLIBCXX_SET 1
#pragma GCC system_header
#include <bits/stl_tree.h>
#include <bits/stl_set.h>
#include <bits/stl_multiset.h>
#include <bits/range_access.h>
#ifdef _GLIBCXX_DEBUG
# include <debug/set>
#endif
#ifdef _GLIBCXX_PROFILE
# include <profile/set>
#endif
#endif /* _GLIBCXX_SET */
It's just a bunch  derivatives of other low-level files! I'm interested in the
derivatives of other low-level files! I'm interested in the 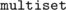 , so it will be logical to visit
, so it will be logical to visit 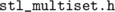 and look at the
and look at the  method:
method:
size_type
count(const key_type& __x) const
{ return _M_t.count(__x); }
which just delegates the task to the 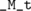 field that is defined at the beginning of the class as
field that is defined at the beginning of the class as
/// The actual tree structure.
_Rep_type _M_t;
and 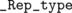 as a typedef for
as a typedef for
/// This turns a red-black tree into a [multi]set.
typedef typename __gnu_cxx::__alloc_traits<_Alloc>::template
rebind<_Key>::other _Key_alloc_type;
typedef _Rb_tree<key_type, value_type, _Identity<value_type>,
key_compare, _Key_alloc_type> _Rep_type;
Red-Black tree. Its definition is contained within 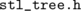 with the true method
with the true method  . At this point, we really have to look at the source code. Conveniently,
. At this point, we really have to look at the source code. Conveniently, 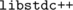 has a GitHub repository (kind of) and the corresponding file that implements
has a GitHub repository (kind of) and the corresponding file that implements 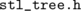 is
is  . The following is the implementation of
. The following is the implementation of  of
of  :
:
template<typename _Key, typename _Val, typename _KeyOfValue,
typename _Compare, typename _Alloc>
typename _Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::size_type
_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::
count(const _Key& __k) const
{
pair<const_iterator, const_iterator> __p = equal_range(__k);
const size_type __n = std::distance(__p.first, __p.second);
return __n;
}
Ignoring all these scary looking templates, we can see that the  method is just three lines long! Namely, in the first line, we get a pair of two iterators, first of which points to the first element in the set with its key equal to
method is just three lines long! Namely, in the first line, we get a pair of two iterators, first of which points to the first element in the set with its key equal to  and the second — to the last. In the second line, we use
and the second — to the last. In the second line, we use 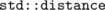 to count elements between the first and the last element
to count elements between the first and the last element  points to. Since
points to. Since  is a balanced binary search tree, we know that if we commit DFS through the tree and write out the nodes in the order of traversal, we will get a sorted sequence. What
is a balanced binary search tree, we know that if we commit DFS through the tree and write out the nodes in the order of traversal, we will get a sorted sequence. What 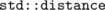 does is just consequently iterates from
does is just consequently iterates from 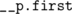 forward and onward until reaches
forward and onward until reaches 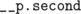 . Since we know that between them are the nodes with the same key, this counting will yield us their total number.
. Since we know that between them are the nodes with the same key, this counting will yield us their total number.
So... std::distance has linear time complexity! It jumps between different locations in memory step-by-step until reaching the "terminal" node. Basically, there's no other way to count nodes within the tree (Although, I know that you can (somehow) invoke custom instance of 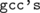 internal tree data structure that will be able to accompany each node with a subtree's
internal tree data structure that will be able to accompany each node with a subtree's 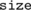 field, which can be used to bring down the complexity of
field, which can be used to bring down the complexity of  up to
up to 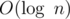 but I need clarification on this).
but I need clarification on this).
The only difference between  and
and 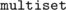 is that
is that 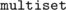 does not depend on the uniqueness of the nodes. Look at these two excerpts from the source code:
does not depend on the uniqueness of the nodes. Look at these two excerpts from the source code:
// Set's insert
std::pair<iterator, bool>
insert(const value_type& __x)
{
std::pair<typename _Rep_type::iterator, bool> __p =
_M_t._M_insert_unique(__x);
return std::pair<iterator, bool>(__p.first, __p.second);
}
and
// Multiset's insert
iterator
insert(const value_type& __x)
{ return _M_t._M_insert_equal(__x); }
The (almost) only difference is that that  uses
uses 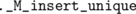 and
and 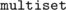
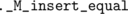 that doesn't care about uniqueness: it will just put there another node with the same key.
that doesn't care about uniqueness: it will just put there another node with the same key.
And... reflecting on this, if we had an array full of ones, for example, to 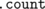 ones with a
ones with a 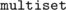 we would need around O(n) time, thus drastically degrading the overall complexity of the algorithm to O(n2)!
we would need around O(n) time, thus drastically degrading the overall complexity of the algorithm to O(n2)!
I don't know if I need to outline the moral of the story or not... Well, I guess, it's pretty straightforward anyway: don't count with multisets!
Have a nice day! Goodbye~~










