Hi. For the next problem I can not think of how to find a solution with graph searches (I thought it was backtraking but my college professor told me that I should use graph searches, which I do not know much about, to solve it).

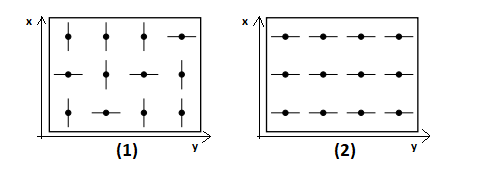
As input we obtain a matrix (3x4) of connections ("|" or "-") which we must decode in the least amount of movements, to avoid that the bomb explodes. As an output inform one of the possible solutions.

The decoding consite in that the matrix must contain only characters "-". To achieve this they tell us that if we move an element of the matrix, both the values ​​of the column and row of the matrix change. For example if I move the element (0,0) of the matrix in this case the "-" change to "|" and vice versa in the column 0 and row 0. In the image (where (1) represents the input matrix and (2) the decoded matrix) a solution to inform would be:

(0,3), (2,1)

How to design an algorithm that solves this problem without using backtraking directly? Thank you in advance

Hi. In the college we are looking at two basic examples of backtracking (sudoku and n-queens) and a question arose: How program the algorithm of the 8 queens in a non-recursive way?

more specifically it must be done through a stack or through a queue counting the steps to reach the solution.

My problem is born with the code they give us and with the algorithm itself (here). I understand that du and dd are the main diagonals but I do not understand the line 16... (specifically du [c + 7 -r]) where that seven comes from(should not move one square per diagonal?).