Ответом на задачу является формула ((a - 1 + b) mod n + n) mod n + 1, где mod n — операция взятия остатка по модулю n.
Итоговая временная сложность решения равна O(1).
Допускается также итеративное решение, каждый раз перемещающее Васю на 1 подъезд в нужном направлении.
Итоговая временная сложность решения равна O(|b|).
Будем рассматривать участников каждого региона отдельно. Отсортируем всех участников из региона в порядке невозрастания баллов. Ответ для данного региона неоднозначен тогда и только тогда, когда участников хотя бы трое и баллы второго и третьего участника совпадают. Иначе ответом является пара из первого и второго участников.
Итоговая временная сложность решения равна 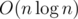 .
.
Наша задача набрать наибольшее количество игрушек, которых ещё нет у Тани так, чтобы их суммарная цена была не больше m. Для этого воспользуемся жадным алгоритмом: будем каждый раз пока нам хватает денег покупать самую дешёвую игрушку, которой ещё нет у Тани. Заведём булевский массив used, чтобы отмечать в нём типы игрушек, которые уже есть у Тани. Очевидно, что на 109 бурлей мы можем купить не более 105 игрушек 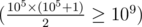 , а значит нам нет смысла рассматривать игрушки с типами больше или равными 2 × 105 (игрушки таких типов из входных данных будем пропускать) и нам хватит массива used размером 2 × 105. Будем идти по типам игрушек в порядке возрастания пока нам хватает денег и, если в массиве used данный тип отмечен значением \texttt{false}, то будем покупать игрушку этого типа.
, а значит нам нет смысла рассматривать игрушки с типами больше или равными 2 × 105 (игрушки таких типов из входных данных будем пропускать) и нам хватит массива used размером 2 × 105. Будем идти по типам игрушек в порядке возрастания пока нам хватает денег и, если в массиве used данный тип отмечен значением \texttt{false}, то будем покупать игрушку этого типа.
Итоговая временная сложность решения составит 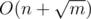 .
.
Если вместо булевского массива использовать тип данных <<множество>> (например, \texttt{std::set} в C++), то можно не пропускать большие значения ai из входных данных. В таком случае временная сложность решения составит 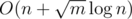 .
.
Из описания трассы следует, что Мария движется таким образом, что вода всегда находится справа от неё. Таким образом, она может упасть в воду только при повороте налево. Для того, чтобы проверить, является ли данный поворот поворотом налево, сопоставим направлениям движения Марии числа: движению на север — 0, движению на запад — 1, движению на юг — 2, движению на восток — 3. Тогда поворот будет поворотом налево, если число для следующего направления dir равно числу предыдущего направления oldDir плюс 1 по модулю 4 (dir ≡ oldDir + 1(mod4)).
Итоговая временная сложность решения равна O(n).
Альтернативное решение. Пусть ответ равен x (это означает, что количество внутренних углов по 270 градусов равно x, а внутренних углов по 90 градусов n - x). Так как сумма внутренних углов n-угольника равна 180 × (n - 2), то можем записать следующее x × 270 + (n - x) × 90 = 180 × (n - 2). Откуда получаем, что 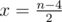 . То есть ответ зависит только от n и не зависит от трассы.
. То есть ответ зависит только от n и не зависит от трассы.
Итоговая временная сложность решения равна O(1).
Во-первых, если граф состоит из нескольких компонент связности, то ответы для них можно считать независимо. Таким образом мы перешли к задаче, когда граф всегда связный. Пусть граф является деревом, тогда мы всегда можем его подвесить и ориентировать все рёбра в порядке обхода dfs'ом. При этом мы сделаем неизолированными все вершины, кроме корня (в подвешенном дереве у каждой вершины, кроме корня, есть единственный предок). Таким образом, ответ в этом случае равен 1. Теперь пусть граф не является деревом, тогда в нём найдётся хотя бы один цикл. Выберем любую вершину на этом цикле и запустим из неё dfs, который ориентирует все рёбра в порядке обхода. Как и в случае с деревом у нас останется только одна изолированная вершина — корень, однако он лежит на цикле и ребро из этого цикла можно ориентировать в него. Таким образом, у нас не останется изолированных вершин и ответ будет равен 0.
Для решения задачи необходимо выделить все компоненты связности и для каждой из них проверить, является ли она деревом. Это можно сделать с помощью dfs или bfs.
Итоговая временная сложность решения равна O(n + m).
В задаче требуется найти связную по сторонам область, произведение количества клеток в которой на минимальное занчение равно заданной величине k. Для этого отсортируем все n × m элементов в порядке невозрастания. Будем последовательно добавлять их в таком порядке, поддерживая при этом компоненты связности. Для этого воспользуемся системой непересекающихся множеств (СНМ, DSU). Кроме того, для каждой компоненты связности необходимо хранить количество клеток в ней. Пусть элемент ai, j только что был добавлен и принадлежит компоненте связности с номеров id. Тогда очевидно, что ai, j — минимум в этой компоненте и если k не делится без остатка на ai, j, то нужной компоненты связности пока получить не удастся. Иначе, посчитаем величину need = k / ai, j — необходимое количество клеток в компоненте связности и если need ≤ CNTid, где CNTid — количество элементов в компоненте связности id, то мы можем найти ответ. Для его поиска запустим из клетки (i, j) dfs, который будет переходить только в клетки больше или равные ai, j и пройдёт ровно need таких клеток.
Итоговая временная сложность решения равна 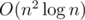 .
.
659G — Забористое разнообразие
Пусть ответ на задачу — это следующая сумма:
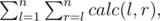
где calc(l, r) — количество способов вырезать верхнюю часть забора так, что её левая граница находится в индексе l, а правая в индексе r. Если l = r (то есть спиливается верхняя часть только одной доски), то calc(l, r) = hl - 1.
Пусть r > l, тогда:
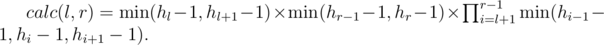
Действительно, число допустимых способов спилить одну доску равно минимуму из высот самой доски и соседних минус один, так как в противном случае нарушится связность спиливаемой части. Крайние доски рассматриваются отдельно, так как у них только по одному соседу. Тогда итоговый ответ на задачу будет выглядеть так:
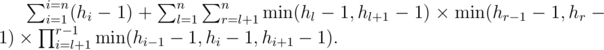
Первое слагаемое вычисляется легко, рассмотрим второе слагаемое. Проведём некоторые преобразования:
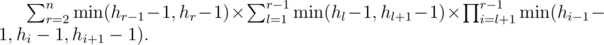
Обозначим
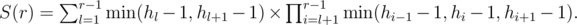
Рассмотрим, как меняется значение S(r) при увеличении r на единицу:
S(r + 1) = S(r) × min(hr - 1 - 1, hr - 1, hr + 1 - 1) + min(hr - 1, hr + 1 - 1).
Таким образом, эту сумму легко поддерживать перебирая r от 2 до n.
Итоговая временная сложность решения равна O(n).









