Jon.Snow's blog

CSES Tree section editorial
By Jon.Snow, 4 years ago, In English

Hello Codeforces,

CSES is a nice collection of classical CP problems which encourages you to learn a lot of basic and advanced concepts. Having editorials would help people to not get stuck on a problem for long. Here are my solutions to the tree section of the problem-set. Looking forward to read corrections/feedback/better solutions in the comment section. Happy coding!

Subordinates

This can be solved using basic DP approach in linear time.
$$$subordinates[u] = \sum\limits_{v:children[u]}^{} subordinates[v]$$$ where v is a child of u

Code

Tree Matching

This problem can be reduced to maximum bipartite matching problem but first we need to split the tree into a bipartite graph. One way to do that is to put all nodes at even depth in the first group and odd ones in the other group. Such a splitting will make sure that we do not have any edges within the same group.

Next, we can use Hopkraft Karp algorithm to find the maximum matching in the bipartite graph created.

Code

Tree Diameter

This is a classical problem having multiple solutions.

One easy to implement solution is using 2 Breadth First Searches (BFS). Start a BFS with a random node and store the last node encountered before search ends. This last node will definitely be one of the ends of the diameter (Why?). Now run a second BFS from this node and you will end on the other end of the diameter.

Code

Tree Distances I

For each node, we want to calculate maximum distance to another node. Previously we saw that that if we start a BFS from any node, we end up on either of the diametric end. We can use this fact to efficiently compute the answer. Let's calculate distances of each node from both the ends of the diameter. Then maximum distance of each node can be calculated as: 

max_distance[u] = max(distance_from_diametric_end1[u], distance_from_diametric_end2[u])
Code

Tree Distances II

We can solve this problem using in-out DP on trees.
$$$in[u]:$$$ sum of distances from u to each node in subtree rooted at u
$$$out[u]:$$$ sum of distances from u to each node excluding the subtree rooted at u

Now, ans[u] = in[u] + out[u]

Calculating $$$in[u]$$$ is quite straightforward. Suppose we want to calculate the sum of distances starting at node u and ending at any node in subtree rooted at v. We can use the pre-calculated value for v and separately add the contribution created by edge $$$u\rightarrow v$$$. This extra quantity will be the subtree size of u. Then we can repeat the process for each child of u.

$$$in[u] = \sum\limits{}{}in[v] + sub[v]$$$ where v is a child of u

To calculate $$$out[u]$$$, first let's calculate the contribution of parent of u. We can use out[par] and add the difference created by the edge $$$u \rightarrow par_u$$$ which is n-sub[par]+1. Next, we add the contribution of all siblings of u combined, considering all paths starting from u and ending in a subtree of one the siblings: in[par]-in[u]-sub[u] + (sub[par]-sub[u]-1).
Finally we have the following formula:

$$$out[u] = out[par] + (n-sub[par] + 1) + in[par]-in[u]-sub[u] + (sub[par]-sub[u]-1)$$$ $$$out[u] = out[par] + n + in[par] - in[u] - 2*sub[u]$$$

Code

Company Queries I

We can solve this problem using binary-lifting technique for finding ancestors in a tree.

For each node x given in a query, we just need to find the $$$k^{th}$$$ ancestor of a given node. We can initialise ans = x and keep lifting our ans for every $$$i^{th}$$$ bit set in k: ans = jump[i][ans] where $$$jump[i][j]$$$ holds $$$i^{th}$$$ ancestor of node $$$j$$$

Code

Company Queries II

This is the classical problem of finding Lowest Common Ancestor which can be solved in multiple ways. One of the common ways is to use binary-lifting which requires $$$O(nlog(n))$$$ preprocessing and $$$O(logn)$$$ per query.

Code

Distance Queries

Distance between node u and v can be calculated as $$$depth[u] + depth[v] - 2*depth[LCA(u,v)]$$$.
LCA of (u,v) can be calculated using binary-lifting approach in $$$O(logn)$$$ per query.

Code

Counting Paths

This problem can be solved using prefix sum on trees.

For every given path $$$u \rightarrow v$$$, we do following changes to the prefix array.

prefix[u]++
prefix[v]++
prefix[lca]--
prefix[parent[lca]]--

Next, we run a subtree summation over entire tree which means every node now holds the number of paths that node is a part of. This method is analogous to range update and point query in arrays, when all updates are preceded by queries.
$$$prefix[u] = \sum\limits_{v:children[u]}^{} prefix[v]$$$

Code

Subtree Queries

This problem can be solved by flattening the tree to an array and then building a fenwick tree over flattened array.

Once reduced to an array, the problem becomes same as point update and range query. We can flatten the tree by pushing nodes to the array in the order of visiting them during a DFS. This ensures the entire subtree of a particular node forms a contiguous subarray in the resultant flattened array. The range of indices corresponding to subtree of a node can also be pre-calculated using a timer in DFS.

Code

Path Queries

This problem can be solved using Heavy-Light decomposition of trees.

First, we decompose the tree into chains using heavy-light scheme and then build a segment tree over each chain. A path from node u to v can seen as concatenation of these chains and each query can be answered by querying the segment trees corresponding to each of these chains on the path. At each node of segement tree, we store the sum of tree node values corresponding to that segment. Since heavy-light scheme ensures there can be at most $$$O(logn)$$$ chains, each query can be answered in $$$O(log^{2}n)$$$ time.

Similarly, each update can be performed in $$$O(logn)$$$ time as it requires update on a single chain (single segment tree) corresponding to the given node.

Code

Path Queries 2

This problem has similar solution as Path Queries. Instead of storing the sum of nodes in segment tree, we store the maximum of node values corresponding to that segment.

Code

Distinct Colors

This problem can be solved using Mo's algorithm on trees and can be reduced to this classical SPOJ Problem

Flatten the tree to an array using the same technique mentioned in solution of Subtree Queries. Then the subtree of each node will correspond to a contiguous subarray of flattened array. We can then use Mo's algorithm to answer each query in $$$O(\sqrt{n})$$$ time with $$$O(n\sqrt{n})$$$ preprocessing.

Code
Alternate solution using small-to-large technique

Finding a Centroid

We can precompute subtree sizes in a single DFS. We can recursively search for the centroid with one more DFS.

Code

Fixed-Length Paths 1

Prerequisite: Centroid Decomposition of a tree

Hint: At every step of centroid decomposition, we try to calculate the number of desirable paths passing through the root(centroid). Since all nodes will eventually become centroid of a subtree, we claim all possible paths are considered. While processing a particular node, we can count the number of nodes at particular depth with cnt[d]++ and use this information to compute our result efficiently.

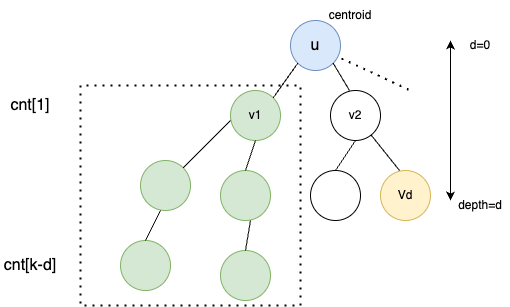
Explanation: Consider the diagram aboce where we are currently solving for tree rooted at $$$u$$$. 
Assuming we have already processed $$$v_{1}$$$ and its subtree. We have updated the cnt array accordingly. While processing node $$$V_{d}$$$, we know it can create $$$cnt[k-d]$$$ new paths of length $$$k$$$. Hence, we add $$$ans += cnt[k-d]$$$.

Once $$$ans$$$ is updated, we can process the subtree of $$$v_{2}$$$ and update $$$cnt$$$ which can be used while processing other children of $$$u$$$.

After processing the whole subtree of $$$u$$$, we decompose the tree by removing the centroid $$$u$$$ and repeat the same process for disjoint trees rooted at $$$v_{1},v_{2}, v_{3}$$$ and so on.

Complexity: Centroid tree has a height of $$$log(n)$$$. Each horizontal layer of tree takes an amortised time of $$$O(n)$$$ as explained above. Thus, total complexity becomes $$$O(n*logn)$$$.

Code

Fixed-Length Paths 2

Approach 1: you can use centroid decomposition here as well but this time sum of all nodes in depth range $$$[k1-d,k2-d]$$$ must be added to $$$ans$$$. This is because all of these nodes will form a path length in range $$$[k1, k2]$$$. This can be done by using a Fenwick tree to calculate range sum efficiently. Although this works in $$$O(n*log^{2}n)$$$, this approach fails CSES time limits.

Code

Approach 2: Prerequisite: Small-To-Large Merging

Instead of using centroid decomposition, we use small-to-large technique to reduce operations. And instead of fenwick tree we use suffix sum arrays to compute range sums efficiently.

For a particular node $$$u$$$ and a particular child $$$v$$$ of $$$u$$$, we maintain suffix sum of count of nodes present at a depth d from u.

$$$suf[i] =$$$ count of nodes having depth in range $$$[i, inf)
$$$

Note that we can combine 2 suffix sum arrays efficiently in $$$O(min(|a|, |b|)$$$ using small-to-large merging technique.

For eg. $$$a=[a_{1},a_{2},a_{3}]
 $$$
$$$b=[b_{1},b_{2}] $$$
can be combined as $$$[a_{1}+b_{1}, a_{2}+b_{2}, a_{3}]$$$

As stated in approach 1, for every node we want to know count of nodes in depth range $$$[k1-d, k2-d]$$$. We can calculate this contribution whenever we are merging smaller suffix sum array to larger one.

Source: https://usaco.guide/problems/cses-2081-fixed-length-paths-ii/solution

Code


End Notes

Full text and comments »

  • Vote: I like it
  • +84
  • Vote: I do not like it

DIGIT DP Tutorial [ITERATIVE]
By Jon.Snow, 4 years ago, In English

Why iterative?

I learned digit DP few years back but only recently I realised that the recursive solution is sometimes hard to debug and difficult to reason about. So this article aims to provide an iterative solution template that can be extended to solve similar problems.

Problem Statement

Find count of numbers in range [L, R] such that sum of its digits is a prime number.

  • $$$1 <= L,R <= 10^{18}$$$

Basic Idea

  • A brute force approach would be to iterate through each number from L to R and check if sum of its digits is prime. This will obviously timeout as constraints are too large.

  • So which particular property can we count such that we don't consume too much time/memory?
    Sum of digits of numbers! Sum of digits of a number cannot exceed 180 for 18 digits, thus we will have to track only 180 states which will save time and memory.This is the key idea behind most digit DP problems: identify and track a property which is finite and will help us reach the answer.

  • We will try to create a function $$$f(x)$$$ which returns all good numbers from $$$[0,x]$$$. Later we can use $$$f(R) - f(L-1)$$$ to find our answer.

Detailed Explanation

  • Let's declare our dp as follows:
    dp[20][2][200]

        20 $$$\rightarrow$$$ maximum number of digits that our dp will support (18 to be precise)
        2 $$$\rightarrow$$$ tight condition (explained later)
        200 $$$\rightarrow$$$ maximum possible sum of digits of a number

        For better understanding, try to think of indexes as $$$dp[i][tight][sum]$$$

  • What does $$$dp[i][tight][sum]$$$ even mean?

    $$$dp[i][0][sum] \rightarrow$$$ count of suffixes that can be formed starting from index i, whose digits add up to $$$sum$$$

    $$$dp[i][1][sum] \rightarrow$$$ count of suffixes that can be formed starting from index i, whose digits add up to $$$sum$$$
    such that the formed suffix is not greater than corresponding suffix in input string


  • Base Cases dp[n][0][0] = dp[n][1][0] = 1
    There exists $$$1$$$ empty suffix with sum of its digits $$$=0$$$

  • We will move from right to left while prepending digits at every index till we finally calculate $$$dp[0][..][..]$$$ which denotes the entire input string

  • What is $$$tight$$$?

    For every state of dp we also need to know if the current suffix formed includes all unbounded numbers or only the numbers less than or equal to $$$suffix_{input}$$$. This information is required because when we are prepending digits to build $$$dp[i]$$$ from $$$dp[i+1]$$$, we will have to choose between bounded/unbounded suffixes based on our current digit. Try to understand this based on the following recurrence relations.

  • We can break $$$dp[i][tight][sum]$$$ into subproblems as follows:

        $$$dp[i][0][sum] = \sum\limits_{d=0}^{9} dp[i+1][0][sum-d] $$$

        $$$dp[i][1][sum] = dp[i+1][1][sum-ss[i]] + \sum\limits_{d=0}^{ss[i]-1} dp[i+1][0][sum-d] $$$

Code

int digit_dp(string ss) {
    int n = ss.size();
 
    //empty suffixes having sum=0
    dp[n][0][0] = 1;
    dp[n][1][0] = 1;
 
    for(int i = n-1; i >=0 ; i--) {
        for(int tight = 0; tight < 2 ; tight++) {
            for(int sum = 0; sum < 200 ; sum++) {
                if(tight) {
                    for(int d = 0; d <= ss[i] - '0' ; d++) {
                        dp[i][1][sum] += (d == ss[i]-'0') ? dp[i+1][1][sum-d] : dp[i+1][0][sum-d];
                    }
                }
                else {
                    for(int d = 0; d < 10 ; d++) {
                        dp[i][0][sum] += dp[i+1][0][sum-d];
                    }
                }
            }
        }
    }
    int ans = 0;
    for(int i = 0; i < 200; i++) {
        if(isPrime(i))
        ans += dp[0][1][i];
    }
    return ans;
}

Complexity

  • As obvious from the loops: $$$O(digits*2*sum*10)$$$

End Notes

  • Find above SPOJ problem here: GONE
Solution GONE
Solution RAONE
Solution Problem D

Full text and comments »

  • Vote: I like it
  • +51
  • Vote: I do not like it