The problem statement:

Given two arrays a and b with sizes n and m respectively. All numbers in these arrays are in the range of 0 to 9 inclusive. Lets create a matrix with size of n x m where values in row i and column j is equal to ai * 10^9 + bj. Find the path from square 1,1 to n,m with the maxium sum. You're allowed to move forward or down.

Input parameters: The first line contains n and m (1 <= n, m <= 100 000)

The second line contains values of array a

The third line contains values of array b

Output Print the maximum sum

Time limit: 1 second

Memory limit: 512MB

Example:

input:

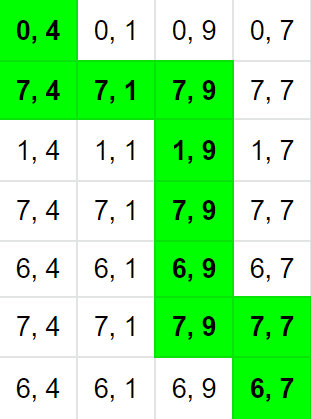
7 4
0 7 1 7 6 7 6
4 1 9 7

output: 55000000068

I tried to solve this problem with dynamic programming, but my solution works in O(n * m) and can't pass time limit:

#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

int main() {
        int n, m; cin >> n >> m;

        vector<uint64_t> a(n), b(m);
        for(int i = 0; i < n; i++) {
        	int tmp;
             cin >> tmp;
             a[i] = tmp * 10e8;
        }

        for(int i = 0; i < m; i++) cin >> b[i];

        vector<uint64_t> dp(m);
        dp[0] = a[0] + b[0];

        for (int i = 1; i < m; i++)
            dp[i] = dp[i-1] + a[0] + b[i];

        for (int i = 1; i < n; ++i) {
            for(int j = 0; j < m; ++j) {
                if (j == 0)
                    dp[j] = dp[j] + a[i] + b[j];
                else
                    dp[j] = max(dp[j], dp[j-1]) + a[i] + b[j];
            }
        }

        cout << dp.back() << endl;

        return 0;
}