Div2A
Алёна счастлива, когда нет незавершенных слоев — то есть перед ней идеальный квадрат с нечетной длиной стороны. Поскольку порядок кусочков фиксирован, достаточно отслеживать общий текущий размер $$$s$$$ головоломки и после каждого дня проверять, является ли $$$s$$$ идеальным квадратом нечетного числа. Самый простой способ сделать это — создать дополнительный массив, содержащий $$$1^2, 3^2, 5^2, ..., 99^2$$$, и проверять после каждого дня, находится ли $$$s$$$ в этом массиве.
Div2B
Найдите символ, который появляется наименьшее количество раз — если есть ничья, возьмите более ранний символ в алфавите. Найдите символ, который появляется наибольшее количество раз — если есть ничья, возьмите более поздний символ в алфавите. Затем замените любой из символов с наименьшим количеством вхождений на символ с наибольшим количеством вхождений.
Div2C
Мы можем разделить столбцы в матрице на три разные группы:
- столбцы, в которых мы проходим через верхнюю ячейку;
- столбцы, в которых мы проходим через нижнюю ячейку;
- столбцы, в которых мы проходим через обе ячейки.
В третьей группе должен быть ровно один столбец — это будет столбец, где мы переходим из верхней строки в нижнюю строку. Все остальные столбцы могут быть распределены между группами $$$1$$$ и $$$2$$$ так, как нам угодно: если мы хотим поместить столбец в первую группу, мы поставим его перед столбцом, в котором мы идем вниз; в противном случае мы поставим его после столбца, в котором мы идем вниз. Таким образом, мы можем получить любое распределение столбцов между первой и второй группой.
Теперь давайте рассмотрим вклад каждого столбца в ответ. Столбцы из первой группы добавляют $$$a_{1,i}$$$ к ответу, столбцы из второй группы добавляют $$$a_{2,i}$$$, столбец из третьей группы добавляет оба этих значения. Таким образом, мы можем перебрать индекс столбца, в котором мы идем вниз, взять $$$a_{1,i} + a_{2,i}$$$ для него, а для всех остальных взять $$$\max(a_{1,j}, a_{2,j})$$$. Это работает за $$$O(n^2)$$$, и в ограничениях задачи этого достаточно.
Но можно решить задачу быстрее — за $$$O(n)$$$. Для этого посчитаем сумму $$$\max(a_{1,j}, a_{2,j})$$$ по всем столбцам. Затем, если мы выберем $$$i$$$-й столбец как столбец, через который мы идем вниз, ответ будет равен этой сумме плюс $$$\min(a_{1,i}, a_{2,i})$$$, поскольку это будет единственный столбец, в котором мы посетим обе ячейки.
Div2D
Первая идея заключается в том, чтобы заметить, что каждый элемент перемещается назад не более одного раза. Действительно, если мы зафиксируем подмножество элементов, которые мы когда-либо перемещаем назад, мы можем выполнить операцию один раз для каждого из них в любом порядке, который нам нравится, и это станет их окончательным порядком с наименьшим возможным увеличением. Оптимальный порядок, конечно, это возрастающий порядок. Вопрос в том, как выбрать это подмножество элементов для перемещения назад.
Поскольку нам нужен лексикографически наименьший массив, мы ищем какой-то жадный подход, который выбирает наименьший возможный элемент на следующей позиции один за другим, слева направо.
- Какое наименьшее число может стоять в начале нашего результирующего массива? Конечно, минимум. Это означает, что все элементы перед минимумом должны быть перемещены назад и увеличены на один.
- Какое наименьшее число мы можем иметь на втором месте, учитывая, что у нас есть минимум на первых позициях? Либо наименьший элемент справа от минимума, либо наименьший элемент среди тех, кто уже перемещен назад.
- ...
Анализируя этот подход, мы видим, что, двигаясь слева направо, мы продолжаем выбирать элементы из последовательности минимумов суффикса и продолжаем увеличивать множество элементов, которые мы должны переместить вправо, чтобы "извлечь" эту последовательность из начального массива. В какой-то момент следующий наименьший элемент приходит не из последовательности минимумов суффикса, а из кучи целых чисел, которые мы перемещаем вправо. В этот момент все оставшиеся элементы должны быть перемещены вправо один раз (то есть увеличены на $$$1$$$), а затем перечислены в отсортированном порядке.
Таким образом, ответ всегда состоит из нескольких первых элементов последовательности минимумов суффикса, начиная с глобального минимума, а затем всех остальных элементов, увеличенных на $$$1$$$ и отсортированных в возрастающем порядке. Чтобы найти точку, где мы переключаемся от последовательности минимумов суффикса к перемещенным элементам, удобно предварительно вычислить минимумы и сохранить множество тех элементов, которые мы уже переместили вправо.
Это решение работает за $$$O(n \log n)$$$, наряду со многими другими.
Div1C
Прежде всего воспользуемся идеей бинарного поиска по ответу. Пусть мы сейчас проверяем, можно ли набрать ответ $$$k$$$.
Переберем все нужные нам координаты вертикальных прямых. Для этого заметим, что есть смысл перебирать только те, у которых прямые совпадают по Y-координате хотя бы с одной из точек. Очевидно, что в таком случае необходимых нам вертикальных прямых будет порядка $$$O(n)$$$.
Во время перебора вертикальной прямой мы будем поддерживать два дерева отрезков на сумму: одно для левой половины плоскости и второе для правой. $$$t_y$$$ в каждом из деревьев отрезков будет означать, сколько есть точек с Y-координатой $$$y$$$ в соответствующей половине плоскости. В каждом из деревьев отрезков посмотрим, можно ли разделить половину плоскости на две части прямой, параллельной оси абсцисс, так, чтобы в обеих частях было хотя бы по $$$k$$$ точек; и, если сделать это можно, то найдем множество подходящих прямых — очевидно, это будет некий отрезок $$$[y_{l}, \, y_{r}]$$$. Если пересечение получившихся отрезков в обоих деревьях отрезков не пустое, то мы нашли ответ. Сделать это можно спуском по дереву за время $$$O(\log n)$$$.
Итак, итоговое время работы описанного решения есть $$$O(n \log^2 n)$$$.
Div1D
Сожмем граф в компоненты сильной связности. Внутри компоненты каждый гонец может перемещаться между любыми парами вершин и тем самым посетить все. Будем теперь решать задачу уже для ориентированного ациклического графа.
Проверим наличие ответа, Предположим, что все гонцы уже знают план победы, и попробуем разослать их так, чтобы каждая вершина была посещена хотя бы раз. Для этого необходимо декомпозировать граф на пути так, чтобы:
- каждая вершина принадлежала хотя бы одному пути;
- в каждой вершине начиналось не больше $$$a[i]$$$ путей (где $$$a[i]$$$ — количество гонцов, изначально находящихся в вершине);
- пути могли пересекаться.
Возьмем исток $$$s$$$ и сток $$$t$$$, путь же теперь можно представить как последовательность $$$s$$$, $$$u_1$$$, ..., $$$u_k$$$, $$$t$$$.
Разделим $$$u$$$ на $$$u_{in}$$$ и $$$u_{out}$$$ и будем считать, что вершина принадлежит $$$u$$$ хотя бы одному пути, если был хотя бы один переход из $$$u_{in}$$$ в $$$u_{out}$$$. Проведем следующие ребра:
- из $$$s$$$ в $$$u_{in}$$$ с пропускной способностью $$$cap = a[u]$$$;
- из $$$u_{in}$$$ в $$$u_{out}$$$ с $$$cap = inf$$$ и условием потока через ребро $$$f \geq 1$$$;
- из $$$u_{out}$$$ в $$$t$$$ с $$$cap = inf$$$;
- из $$$u_{out}$$$ в $$$v_{in}$$$ с $$$cap = inf$$$ для всех рёбер (u, v) в исходном графе.
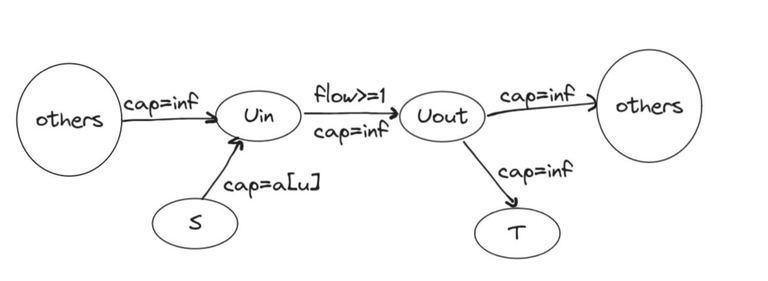
Что и эквивалентно нахождению потока с ограничениями в данном графе.
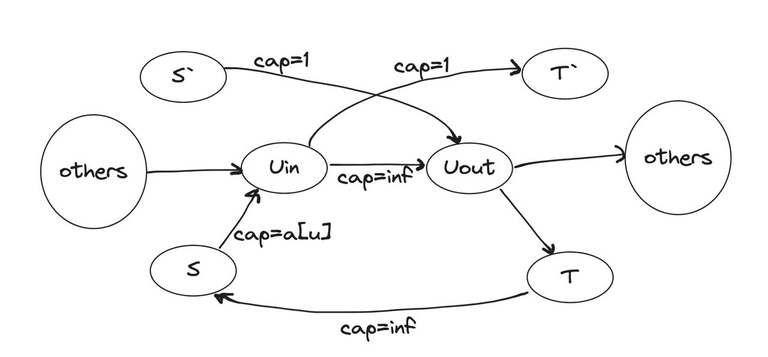
Для этого создадим фиктивный исток $$$s'$$$ и сток $$$t'$$$, теперь для каждого ребра $$$(u_{in}, u_{out})$$$ c потоком через него $$$1 \le f \le inf$$$ сделаем следующую замену, проведя ребра:
- из $$$u_{in}$$$ в $$$u_{out}$$$ с $$$cap = inf - 1$$$;
- из $$$s'$$$ в $$$u_{out}$$$ с $$$cap = 1$$$;
- из $$$u_{in}$$$ в $$$t'$$$ с $$$cap = 1$$$;
- из $$$t$$$ в $$$s$$$ с $$$cap = inf$$$.
Нахождение потока удовлетворяющего ограничениям эквивалентно нахождению максимального потока из $$$s'$$$ в $$$t'$$$, и если он равен количеству вершин, то значит ответ гарантированно существует, иначе можно вывести $$$-1$$$ уже на этом шаге.
Теперь минимизируем количество гонцов, которым изначально известен план. Заметим, что:
- нет смысла гонцам перемещаться, пока не узнают план;
- нет смысла передавать план более чем одному гонцу из одного города.
Пробуем учесть это при построении. Вместо добавления рёбер из истока в $$$u_{in}$$$ поступим так:
- создадим вершину $$$u_{cnt}$$$ для контроля количества гонцов и проведём рёбра:
- из $$$s$$$ в $$$u_{cnt}$$$ с $$$cap = a[u]$$$;
- из $$$u_{cnt}$$$ в $$$u_{out}$$$ с $$$cap = a[u]$$$;
- из $$$u_{cnt}$$$ в $$$u_{in}$$$ с $$$cap = 1$$$, $$$cost = 1$$$.
- всем остальным рёбрам зададим нулевую стоимость.
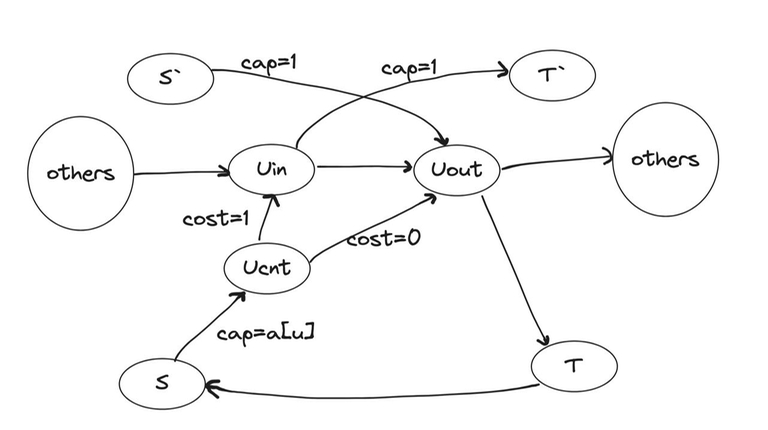
Что в свою очередь эквивалентно тому, что в результате все $$$a[i]$$$ гонцов узнают план, но, если в наш город никто не пришел, то собственноручно расскажем ровно одному гонцу из этого числа заплатив при этом $$$cost=1$$$ человека.
Ответом на задачу является минимальная стоимость максимального потока из $$$s'$$$ в $$$t'$$$ при таком построении графа. Доказательство следует из построения графа.
MCMF можно считать за $$$O(n^2m^2)$$$ или $$$O(n^3m)$$$ для любых графов, но в стоит заметить, что величина потока f ограничена n и имеем решение за $$$O(fnm)$$$ при использовании Форда-Беллмана или $$$O(fm\log n)$$$ при использовании Дейкстры с потенциалами.
Из интересного, заметим что в результате получили $$$3n$$$ вершин и $$$m + 7n$$$ ребер. При аккуратном написании MCMF вполне укладывается в TL.
Div1E1+E2
Для удобства номы будем называть группами, включающими какие-то города.
Ключевым условием является то, что каждой специализации может соответствовать не более одной задачи. Тем самым города из разных групп должны иметь "практически отсортированное" значение силы при увеличении порядкового номера группы.
Обозначим за $$$[l_i, r_i]$$$ отрезок, включающий все силы городов в группе $$$i$$$, где $$$r_i$$$ — максимальная сила города из этой группы, а $$$l_i$$$ — минимальная. При $$$l_i \le r_{i+2}$$$ невозможно построить контест, так как между городами соответствующим $$$l_i$$$ и $$$r_{i+2}$$$ должна быть разница хотя бы в 2 задачи, но они могут отличаться максимум на 1 задачу по специализации. После этого задача сводится к рассмотрению двух соседних групп и последующей проверки сложностей задач на соответствие линейным условиям каждой группы.
Рассмотрим 2 случая:
При $$$l_i \ge r_{i+1}$$$ для соблюдения порядка достаточно добавить несколько задач (а точнее всего 2) сложности из отрезка $$$[r_{i+1} + 1, l_i]$$$.
В противном случае каждый город $$$i$$$-й группы, лежащий в пересечении, должен решить задачу со своей специализацией. При этом ни одна задача не может быть в отрезке $$$[l_i + 1, r_{i+1}]$$$, так как город, имеющий наибольшую силу в группе $$$i+1$$$, решит не меньше задач, чем самый слабый город $$$i$$$-й группы, чего нам допускать нельзя. Для соблюдения порядка с остальными группами достаточно добавить 2 задачи сложности $$$r_{i+1} + 1$$$ (в отличие от первого случая, в силу того, что не может быть $$$l_i \le r_{i+2}$$$, здесь можно сразу определить подходящую сложность задач, но их можно будет расставить по тому же алгоритму, что и для 1-го случая).
Можно заметить, что при добавлении двоек задач им нужно выбирать не используемую никем спецификацию (так как мы ее в принципе не используем, но иначе это может породить коллизии).
Получаем, что нам необходимо расставить задачи с заданной спецификацией, которую сможет решить город из пересечения групп, то есть ее сложность должна быть не больше мудрости этого города, а так же расставить по 2 задачи некоторых сложностей для соблюдения порядка между группами. Эти трудности появляются из-за возможного пересечения с другими группами при использовании $$$r_{i+1} + 1$$$ как сложности задачи и возможных коллизий спецификаций городов, из-за чего город из слабой группы может решить задачу, которую мы для него не предполагали, тем самым нарушив условия строгости между группами.
Большая часть проблем не может возникнуть при $$$m=2$$$, поэтому сказанное выше уже является решением (без небольших доработок) простой версии задачи.
Сначала решим, как выбрать сложность для задач с определенной спецификацией. Для этого запретим использовать спецификацию задач, соответствующую городам, которые образуют 2-й случай (то есть из $$$i+1$$$-й группы), со сложностью $$$[l_i, b_j]$$$, где j — номер такого города. Также, как было указано, мы не можем иметь вне зависимости от типа задачу из отрезка $$$[l_i + 1, r_{i+1}]$$$. Для определения сложности достаточно ее выставить максимально возможной (равной мудрости) и затем постепенно снижать, пока не попадем в разрешенную сложность.
Чтобы разрешить проблему из первого случая, поставим барьеры по 2 задачи со сложностью, равной силе некоторого города везде, где это возможно.
Если для данной конфигурации существует ответ, то мы его таким образом гарантированно построим, использовав не более $$$3 \cdot n$$$ задач. После всех вычислений нужно проверить, удовлетворяет ли построенный нами контест условиям задачи, и вывести -1 в противном случае.
Div1F1
Можно заметить, что если строка содержит правильное количество количество символов 'Y', 'D', 'X' и не имеет двух подряд идущих одинаковых символов, то её можно получить при помощи заданных операций.
Чтобы показать это, приведем алгоритм, который построит некоторую последовательность операций, приводящих к заданной строке. Пойдем с конца (со строки, которую хотим получить к пустой строке) постепенно откусывая символы.
Посмотрим на текущую строку. Не умаляя общности, пусть первый её символ равен 'Y'. Тогда в строке должна встречаться строка 'DX' и/или строка 'XD'. Это верно потому что для отсутствия 'DX' и 'XD' необходимо чтобы между любой парой символов не равных 'Y' находился хотя бы один символ 'Y'. Этого, в лучшем случае, можно добиться поставив 'Y' через каждый символ. Таким образом, символов не равных 'Y' при наличии $$$n-1$$$ 'Y' можно поставить не более $$$n$$$. Но $$$3n-1>n$$$ при $$$n>0$$$.
Получается, что строка имеет вид 'Y...ADXB...'.
Если A $$$\neq$$$ B, мы можем удалить символы 'Y', 'D', 'X' и ничего не сломаем.
Если A = B, то A = B = 'Y', так как A != 'D' и A != 'X'.
Тогда строка имеет вид 'Y...YDXY...', и мы можем удалить подстроку 'YDX' и останется все еще несломанная строка 'Y...Y...'.
Div1F2
Выделим из строки подотрезки, полностью состоящие из '?'. Для каждого обозначим его длину за $$$len_i$$$ и два соседних символа (стоящих слева и справа) за $$$l_i$$$, $$$r_i$$$. (Если правый и/или левый символ отстуствуют, возьмем их за '#', как символ, не совпадающий ни с каким из нас интересующих.
Выпишем тривиальные ограничения на количество доступных символов каждого вида на отрезке. Очевидно, что символов каждого вида не может быть больше, чем $$$\frac{len_i+1}{2}$$$: поставим по одному символу через каждый символ. Но если, например, слева у нас стоял символ 'Y', то количество позиций, где мы можем поместить 'Y' сокращается на $$$1$$$. Итого мы можем поставить не более $$$\frac{len+1-(l_i=b)-(r_i=b)}{2}$$$ символов типа b. Выпишем такие ограничения для каждого типа символов и обозначим их за $$$Y, D, X$$$ соответственно.
Оказывается, что мы можем расставить $$$y$$$ символов 'Y', $$$d$$$ символов 'D' и $$$x$$$ символов 'X', тогда и только тогда, когда $$$y+d+x=len_i$$$ и $$$0\leq y \leq Y, 0 \leq d \leq D, 0 \leq x \leq X$$$. Это можно доказать по индукции или проверить стрессом на небольших значениях. Отсюда заключаем, что чтобы мы имели возможность расставить $$$x, d, y$$$ символов каждого вида, надо чтобы выполнялись неравенства выше.
Из равенства $$$y+d+x=len_i$$$ выразим $$$d=len_i - (x+y)$$$.
Получаются три ограничения: $$$0\leq x \leq X, 0 \leq y \leq Y, 0 \leq len_i - (x+y) \leq D$$$. Первые два образуют прямоугольник, а третье отрезает от него два угла под углом $$$45$$$ градусов. А это выпуклый многоугольник.
Получается, что если для каждого отрезка из '?' выписать многоугольник и просуммировать их суммой Минковского, получатся ограничения на всю строку.
Так как в сумме минковского (после склеивания колиннеарных подряд идущих отрезков) будет не более 6 точек, можно написать жадный алгоритм, который каждому '?' последовательно пробует сопоставить нужный символ.
Итоговая асимптотика $$$O(n)$$$ с некоторой констаной.










