First of all, congratulations to jqdai0815 for winning, LHiC and jcvb for coming second and third. The Final Round proved to be quite challenging, and we are happy that the results are tight.
The round was prepared by Aksenov239, GShark, izban, manoprenko, niyaznigmatul, qwerty787788 and SpyCheese, supervisor andrewzta. Special thanks for this round goes to izban who is the author of problems D, E and F, and also gave a lot of important comments for all problems of the round.
Now let us move on to the editorial.
First let us prove that the answer is always YES.
Let us iterate over bj and check if summing it up with all ai values don't result in values that we already have. If no conflict is found, add the corresponding bj to B.
Let us give some estimate for the maximum element of B. The reason that we cannot include bj2, to B is the equality ai1 + bj1 = ai2 + bj2, so bj2 = bj1 - (ai2 - ai1). Each element of B forbids O(n2) values, so max(B) is O(n3). That means that the answer always exists for the given constraints.
Now let us speed up the test that we can add a number to B. Let us use an array bad, that marks the numbers that we are not able to include to B. When trying the value bj, we can add it to B if it is not marked in bad. Now the numbers that are equal to bj + ai1 - ai2 are forbidden, let us mark them in bad. The complexity is O(n3) for each test case.
Let us consider the following similarity graph: the vertices are the prefixes of the given words, two vertices are connected by an edge if the corresponding words are similar. Note that the set of vertices in this graph is the same as in the trie for the given words, so it doesn't exceed the sum of lengths of words.
Let us prove that the resulting graph is a forest. If two words are similar, let us call the shorter one the parent of the longer one. Each vertex now has at most one parent, and there are no cycles, so the graph is a set of trees — a forest.
Now the required set is the independent set in the constructed similarity graph, so we can use dynamic programming or greedy algorithm to find it.
There are two ways to construct the similarity graph.
Way 1. Hashes For each prefix find its hash, make a set of all hashes. Now for each prefix remove its first letter, check if such hash exists. If it does, connect them by an edge.
Way 2. Aho-Corasick
Let us build Aho-Corasick automaton for the given set of words. The vertices of the similarity graph are automaton vertices. An edge exists between two vertices if the suffix link from one of them goes to the other one, and their depths differ by exacly 1.
Let us use divisibility rule for eleven. The number is divisible by eleven if the sum of digits at odd positions is equal to the sum of digits at even positions modulo 11. So for each number on a card there are only two parameters that we care about: the sign interchanging sum of its digits with digits at odd positions positive and digits at even position negative, and the parity of its digit count.
Let us divide all cards to two groups: with even digit count and with odd digit count. Let us first put cards with numbers that have odd count of digits. Half of them (rounded up) will have their sign interchanging sum used as positive, other half as negative. Let us use dynamic programming to find the number of ways to sum them up to have a given sum modulo 11. The state includes the number of cards considered, the number of cards that are used as positive, and the current sum modulo 11. There are two transitions: take the current card as positive, and take it as negative.
If there are no cards with odd digit count, no matter how you order even digit count cards the result modulo 11 is the same. So the answer is either 0 or n!. In the other case each even digit count card can be used either as positive, or as negative, independent of the other cards. Use analogous dynamic programming to count the number of ways to get each possible sum modulo 11.
Finally, combine results for even and odd digit count cards, getting the total sum modulo 11 equal to 0.
Time complexity is O(n2).
Let us use dynamic programming for a rooted tree and some data structures. Denote as fv the maximal total beauty of edges that have both ends in a subtree of v, such that if we add them all to the subtree it would be a cactus.
To calculate fv let us consider two cases: v belongs to some cycle, or it doesn't. If it doesn't belong to any cycle, fv is equal to the sum of fu for all children u of v.
If v belongs to a cycle, let us iterate over all possible cycles it can belong to. Such cycle is generated by an added edge (x, y) such that LCA(x, y) = v. Try all possible such edges and then temporarily delete a path from x to y from a tree, calculate the sum of fu for all u — roots of the isolated subtrees after the deletion of the path, and add it to the beauty of (x, y).
Now we have an O(nm) solution.
To speed up this solution let us use some data structures. First, we need to calculate LCA for all endpoints of the given edges, any fast enough standard algorithm is fine. The second thing to do is to be able to calculate the sum of fu for all subtrees after removing the path. To do it, use the following additional values: gu = fp - fu, where p is the parent of u, and sv = sum(fu), where u are the children of v.
Now the sum of fu for all subtrees after x - y path removal is the sum of the following values: sx, sy, sv - fx' - fy', the sum of gi for all i at [x, x'), the sum of gi for all i at [y, y'), where x' is the child of v that has x in its subtree, and y' is the child of v that has y in its subtree. We need some data structure for a tree that supports value change in a vertex and the sum for a path, range tree or Fenwick are fine. The complexity is O((n + m)log(n)).
Any point X can be given by two angles α = XAB and β = XBA.

The point (α2, β2) is in coverage area of a satellite at the point (α1, β1), if α2 ≤ α1 and β2 ≤ β1.
Let two satellites that want to create a communication channel are at points (α1, β1) and (α2, β2). Repeater must be positioned in such point (α0, β0), that α0 ≤ min(α1, α2) and β0 ≤ min(β1, β2). To make it harder for it to get to other satellites coverage area, it is reasonable to maximize α0 and β0: α0 = min(α1, α2), β0 = min(β1, β2).
Now let us move to a solution. Consider a query of type 3: you are given two satellites at points (α1, β1) and (α2, β2). You must check whether the point (α0, β0) = (min(α1, α2), min(β1, β2)) is not in the coverage area of any other satellite. That means that among all satellites with α ≥ α0 the maximum value of β is smaller than β0.
The solution is offline, it considers all satellites from the test data and just turns them on and off. Sort all satellites by α. Each moment for each satellite we store its β if it exists, or - ∞ if it doesn't. Let us build a range tree for maximum, and update values as satellites come and go. The query is a range maximum. To avoid considering the satellites from the query, change their values to - ∞ before the query, and restore them afterwards.
The next thing to do is to get rid of floating point numbers. Instead of calculating the angle values, we will only compare them using cross product. Similarly, instead of storing β values in range tree, we will store indices and compare them by cross product in integers.
The final remark: we need to check that the point (α0, β0) is not inside the planet. The point is inside the planet, if the angle AXB is obtuse, that can be checked by a scalar product of XA and XB. The point X can have non-integer coordinates, so we will not look for it, but will use colinear vectors from among those connecting satellite points to A and B.
We give the main ideas of the solution, leaving proofs as an exercise.
Let us introduce coordinates y(x), where x = exp1 - exp2, and y = exp1 (exp1, exp2 — experience of the first and the second player, respectively). Let us proceed with time, and keep the set of possible states at this plane. It is a polygon.
Lemma 1: in the optimal solution if at some moment both players can play the game simultaneously, they should do so.
Now consider all moments of time, one after another. There are three transitions that modify the polygon:
- The first player can play for t seconds. The new polygon is the Minkowski sum of the previous polygon and the degenerate polygon: segment with two vertices (0, 0) and (t, t).
- The second player can play for t seconds. The new polygon is the Minkowski sum of the previous polygon and the segment with vertices (0, 0) and ( - t, 0).
- Both players can play for t seconds. Now all points with x-coordinates [ - C;C] have 2t added to their y coordinate, and other points have t added to their y coordinate.
Let us now see how the polygon looks like. It is x-monotonous polygon (each line parallel to y-axis intersects it via a segment), the lower bound of this polygon is y = 0 if x ≤ 0 and y = x if x > 0. Let us see how the upper bound of the polygon looks like.
We want to prove that y-coordinate of the upper bound of the polygon doesn't decrease, and it only contains segments that move by vectors ( + 1, 0) and ( + 1, + 1).
We attempt an induction, and the induction step is fine for the first two transitions. But the third transition can make the upper bound non-monotonous at a point x = C. To fix it, let us change the definition of our polygon.
Instead of storing all possible reachable points, we will keep larger set, that contains the original set, and for each of its point we can get maximal experience for the first player not greater than what we could originally get.
Lemma 2: if at some moment t we take two points P1 = (x1, y1) and P2 = (x2, y2) such that C ≤ x1 ≤ x2, and y1 ≥ y2, and our player start training from those states, the maximal experience for point P2 is not greater than for the point P1.
So we can expand our upper bound for x from [C; + inf) by a maximum value of the correct upper bound and y = y(C). The similar proof works for a line y = y(C) - (C - x) for x in ( - inf;C].
Now we have an upper bound as a polyline that contains ( + 1, 0) and ( + 1, + 1) segments. All is left to do is to modify the polyline using the described transitions. This can be done using some appropriate data structure, treap for example. The solution works in O(nlog(n)).








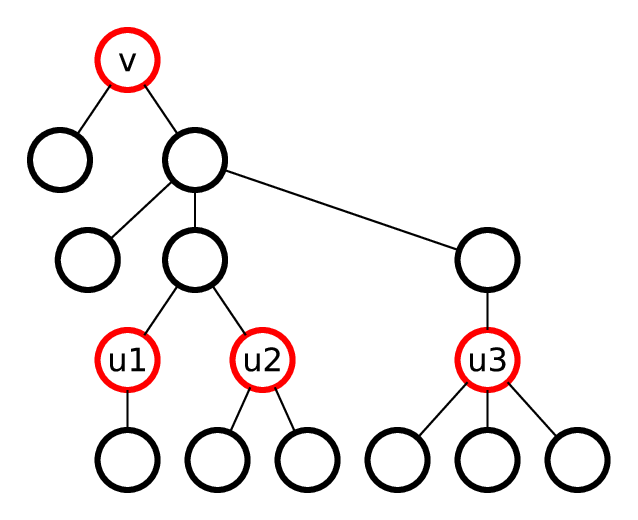


 . To prove the complexity notice that for each vertex when it is in the smaller component, the size of the component at least halves. So it can only happen
. To prove the complexity notice that for each vertex when it is in the smaller component, the size of the component at least halves. So it can only happen  times.
times.
