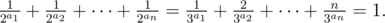День первый.
1. Дан треугольник ABC; точка J является центром вневписанной окружности, соответствующей вершине A. Эта вневписанная окружность касается отрезка BC в точке M, а прямых AB и AC — в точках K и L соответственно. Прямые LM и BJ пересекаются в точке F, а прямые KM и CJ — в точке G. Пусть S — точка пересечения прямых AF и BC, а T — точка пересечения прямых AG и BC.
Докажите, что точка M является серединой отрезка ST.
2. Дано целое число n ≥ 3 и действительные положительные числа a2, a3, ..., an, удовлетворяющие соотношению a2, a3... an = 1. Докажите, что
(a2 + 1)2(a3 + 1)3...(an + 1)n > nn.
3. Два игрока A и B играют в игру Угадай-ка. Правила этой игры зависят от двух положительных целых чисел k и n, и эти числа известны обоим игрокам.
В начале игры A выбирает целые числа x и N такие, что 1 ≤ x ≤ N. Игрок A держит число x в секрете, а число N честно сообщает игроку B. После этого игрок B пытается получить информацию о числе x, задавая A вопросы следующего типа: за один вопрос B указывает по своему усмотрению множество S, состоящее из целых положительных чисел (возможно, это множество уже было указано в одном из предыдущих вопросов) и спрашивает игрока A, принадлежит ли число x множеству S. Игрок B может столько вопросов, сколько он хочет. На каждый вопрос игрока B игрок A должен сразу ответить да или нет, при этом ему разрешается соврать столько раз, сколько он хочет; единственное ограничение состоит в том, что из любых k + 1 подряд идущих ответов хотя бы один ответ должен быть правдивым.
После того, как B задаст столько вопросов, сколько он сочтет нужным, он должен указать множество X, содержащее не более чем n целых положительных чисел. Если x принадлежит X, то B выиграл; иначе B проиграл. Докажите, что:
1) Если n ≥ 2k, то B может гарантировать себе выигрыш.
2) Для всякого достаточно большого k найдется целое число n ≥ 1, 99k, при котором B не сможет гарантировать себе выигрыш.
День второй.
4. Найдите все функции
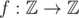такие, что для всех a + b + c = 0 : f(a)2 + f(b)2 + f(c)2 = 2f(a)f(b) + 2f(b)f(c) + 2f(c)f(a).
5. Пусть ABC — треугольник с
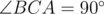и D — основание высоты, опущенной из вершины C. Пусть X — некоторая точка внутри отрезка CD. K — точка на отрезке AX такая, что BK = BC. Аналогично, L — точка на отрезке BX такая, что AL = AC. Пусть также M — точка пересечения AL и BK.Докажите, что MK = ML.
6. Найдите все натуральные числа n, для которых существуют неотрицательные целые числа a1, a2, ..., an такие, что:
