It is sad that
marzipan tried to convince others to write the blog goodbye 23 to get contribution.
but his blog got -3500 [so far]
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
It is sad that
marzipan tried to convince others to write the blog goodbye 23 to get contribution.
but his blog got -3500 [so far]
Hi, Is there a way to download my submitted file using the Codeforces API?
i use this but not working
PLEASE HELP
hey I wanted to get the most upvoted post in CF but I got negative contrib.
so I decided to get the most down voted post on CF.
please help me :((
Hi ^~^
1.1 — power-Function:
[Binary Exponentiation] is a trick which allows to calculate $$$a^n$$$ using $$$O(\log n) $$$
The idea is that we can traverse through all the bits of a number from LSB to MSB in $$$O(\log n) $$$ time.
Write $$$n$$$ in base $$$2$$$.
The number has exactly $$$ \lfloor \log_2 n \rfloor + 1 $$$ digits in base 2, we only need to perform $$$O(\log n) $$$ multiplications, if we know the powers $$$a^1, a^2, a^4, a^8, \dots, a^{2^{\lfloor \log n \rfloor}}$$$ .
int dnt_pow(int a, int b, int md = mod)
{
int pw_ans = 1;
while(b)
{
if(b&1)
{
pw_ans = (a*pw_ans)%md;
}
a = (a*a)%md;
b >>= 1;
}
return pw_ans ;
}
1.2 — GCD-Function:
[Euclidean algorithm] is a trick which allows to calculate $$$gcd(a,b) $$$ using $$$O(\log \min(a, b))$$$ The idea is that subtract the smaller number from the larger one until one of the numbers is zero.
For Time Complexity and Binary GCD you can read This.
int dnt_gcd(int a, int b)
{
return b ? gcd(b,a%b):a ;
}
Note that you can calculate $$$lcm(a,b)$$$ with $$$\frac{a}{gcd(a,b)}\ * b $$$
1.3 — Factorial & nCr & ...:
Sometimes you need to calculate $$$\binom n k $$$
For that first we precompute all factorials modulo $$$ mod $$$ with $$$O(N)$$$.
void dnt_bld()
{
fac[0] = 1;
for(int i = 1 ; i < N ; i++)
{
fac[i] = (fac[i-1] * i) % mod;
}
}
int dnt_ncr(int n,int r)
{
return fac[n] * inverse(fac[r] * fac[n - r] % mpd) % mod;
}
BUT WE CAN PRECOMPUTE INVERSE OF FAC[I] IN $$$ O(Nlogmod) $$$
void dnt_bld()
{
fac[0] = 1;
inv[0] = dnt_pow(fac[0],mod-2);
for(int i = 1 ; i < N ; i++)
{
fac[i] = (fac[i-1] * i) % mod;
inv[i] = dnt_pow( fac[i] , mod-2);
}
}
int dnt_ncr(int n,int r)
{
return fac[n] * inv[r] % mod * inv[n-r] % mod;
}
1.4 Fibonacci in 20 line:
as you know you can calculate $$$n-th$$$ Fibonacci number with matrix.
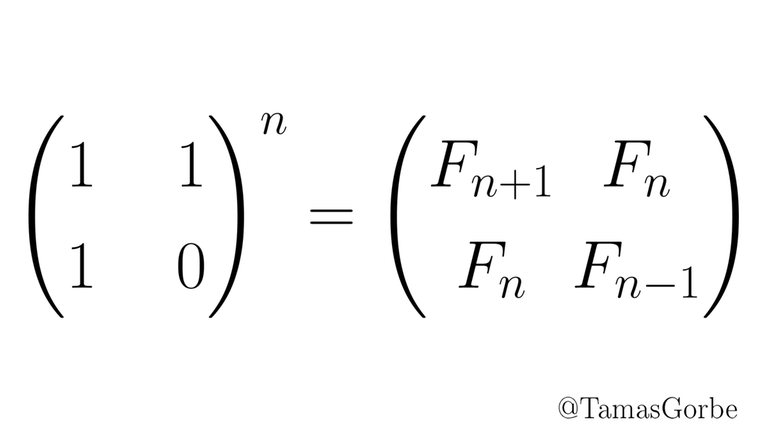
it can be proved that :
F[2*n — 1] = F[n]*F[n] + F[n — 1]^2
F[2*n] = (F[n — 1] + F[n + 1])*F[n] = (2*F[n — 1] + F[n])*F[n]
map<long, long> fib;
int dnt_fib(int n)
{
if (fib.count(n)) return fib[n];
if (n % 2 == 0)
{
return fib[n] = ( dnt_fib(n/2)*dnt_fib(n/2) + dnt_fib(n/2-1)*dnt_fib(n/2-1) ) % mod;
}
else
{
return fib[n] = ( dnt_fib(n/2 + 1) * dnt_fib(n/2) + dnt_fib(n/2 - 1) * dnt_fib(n/2) ) % mod;
}
}
int solve()
{
fib[0] = 1;
fib[1] = 1;
int n;
cin >> n;
cout << (n==0 ? 0 : dnt_fib(n-1)) << endl;
}
tnx kien_coi_1997 and I_love_tigersugar
1.5 Built-in useful function:
vector<int> a(n);
iota(a.begin(), a.end(), 1);
// a = 123..
random_shuffle(a.begin(), a.end());
// a = random permutation of a
vector<int> ps(n);
partial_sum(a.begin(), a.end(), ps.begin());
// ps[i] = a[0] + a[1] + .... a[i-1] + a[i] ( ps[i] = ps[i-1] + a[i])
vector<int> h(n);
adjacent_difference(a.begin(), a.end(), h.begin());
// h[0] = a[0]
// (i>0) h[i] = = a[i] - a[i-1]
cout << accumulate(a.begin(), a.end(), x) ;
//cout x + a[0] + a[1] + a[2] + ... + a[n]
cout << inner_product(a.begin(), a.end(), b.begin(), 234) << "\n";
// x = 234 + sum(a[i] * b[i])
tnx Igorjan94 for this
Was this blog helpful?
Hello ^^
I have seen many TODO editorials after 10-11 years.
Can it be completed?
and so on
Hi today this user used public computer and didn't log out of his account afterward, so we are writing this blog to educate people about importance of logging out :)
Hi^^,
Can someone explain me the problem of SEERC2020 — Problem I? [I didn't understand the editorial]
And share the code if possible.
Link of problem : PROBLEM I
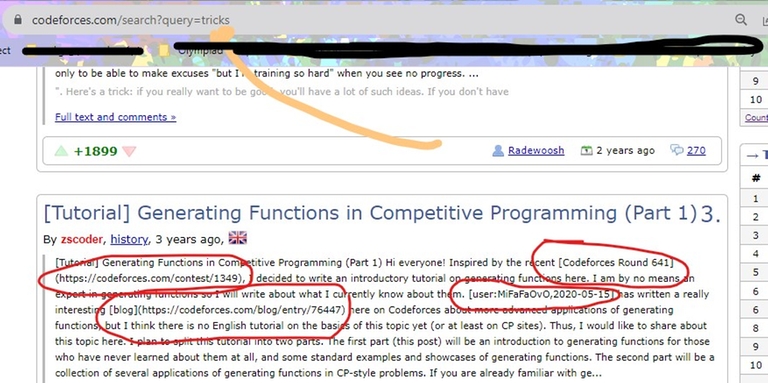
Hi ,
I was looking at blogs with tricks tag when I came across something interesting.
on the page that is specified for each tag and shows the blogs of that topic; The preview for any blog is the message that is written — not the message that needs to be displayed — .
Look at the picture below to see what I mean.
In your opinion, what is the most important factor for a good Contest? and can u share a some good contest?
| Название |
|---|


