Задача А
Разберем два случая t = 10 и t ≠ 10.
Если t = 10, то либо n = 1, и тогда ответ - 1 (очевидно, что среди чисел от 1 до 9 нет делящихся на 10), либо n > 1, и тогда первые n - 1 цифр можно заполнить как угодно, а в конце дописать 0.
Если t < 10, то просто заполним все число цифрами t и оно, очевидно, будет делиться на t.
Задача B Количество способов рассадить всех гномов — 33n. Посчитаем количество способов рассадить гномов так, чтобы в любом треугольнике гномы получили 6 монет, а потом вычтем это число из всех способов. Заметим, что все гномы однозначно разбиваются на треугольники вида i — (i + n) — (i + 2n), i < n. Поэтому можно посчитать количество способов независимо по каждому треугольнику, а потом перемножить результаты. Чтобы получить ответ для треугольника, осталось заметить, что существует ровно 7 способов взять гномов с 6 монетами (это все перестановки 1, 2, 3 и 2, 2, 2)
Итого ответ — 33n - 7n. Посчитать степени можно за O(n).
Задача С
Построим строку, которая не отличается на t, а совпадает в k = n - t символах. Пусть строки s1 и s2 совпадают в q символах. Тогда если k ≤ q, то возьмем любые k позиций, в которых s1 и s2 совпадают, и поставим в ответ такие же символы. Во все остальные n - k позиций поставим символы, отличающиеся от соответствующих в s1 и s2 (мы всегда можем так сделать, так у нас 26 букв).
Теперь k > q. Тогда, если есть ответ, в котором в какой-то из этих q позиций в ответе стоит не такой же символ, как в s1 и s2, то сделаем его равным им, а в каких-нибудь позициях, где s1i ≠ s2i, s1i = ansi (и наоборот) поставим в ansi символ, отличный от s1i и s2i(это можно сделать, так как k > q). Тогда можно сразу в эти q позиций поставить символы, равный соответствующим в s1 и s2. Теперь у нас есть строки s1 и s2 длины n - q, отличные в каждой позиции, и надо предъявить строку ans такую, что f(ans, s1) = f(ans, s2) = k - q. Так как строки s1 и s2 отличаются во всех позициях, то любой символ из ans равен либо соответствующему в s1, либо соответствующему в s2, либо ни одному из них. Поэтому, нам надо хотя бы 2(k - q) символов в ответе, чтобы сделать f(s1, ans) = k - q и f(s2, ans) = k - q. Следовательно, если n - q < 2(k - q), то решения не существует. Иначе просто жадно в первые k - q символов ответа поставим символы из s1, в следующие k - q символы из s2, а остальные заполним символами не из s1 и не из s2.
Асимптотика — O(n).
Задача D
Общеизвестно, что между двумя соседними простыми числами, которые меньше 109, расстояние не очень большое. На самом деле для n = 109 максимальное из этих расстояний равно 282. Поэтому будем делать так: найдем наибольшее число p, такое что p < n - 1 и p — простое. По нашему утверждению n - p < 300. Скажем, что p входит в разложение n и теперь надо разложить четное(так n — нечетное и p — нечетное(если не 2)) n - p на сумму двух простых. Так как n - p маленькое, то сделаем это, просто перебрав два простых. То, что для всех четных, меньших 300, существует разложение на не более чем два простых, можно было проверить просто написав перебор.
Задача E
Будем считать, что все мы платим за обмен не |i - j|, а 2|i - j|. Тогда можно считать, что мы платим |i - j| за перемещение pi и |i - j| за перемещение pj. Тогда, если x изначально был на позиции i, а потом пришел на позицию j, то мы заплатим за него хотя бы |i - j|. Поэтому ответ это хотя бы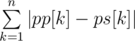 
(pp — позиция k в перестановке p, а ps — позиция k в перестановке s). Докажем, что это и есть ответ конструктивно, предъявив алгоритм.
Будем считать, что перестановка s отсортирована (нашу задачу легко свести к этой). Тогда будем последовательно(сначала n, потом n - 1 и так далее) переставлять числа на свои позиции. Как поставить n на свою позицию? Пусть оно стоит на позиции pos. Докажем, что среди чисел, стоящих справа от n, есть число, меньшее или равное pos(дальше поменяем его местами с n — от этого оба числа сдвинутся к своим итоговым позициям, и при этом n сдвинется хотя бы на 1 вправо, поэтому можно дальше делать так же). Заметим, что всего справа от n ровно n - pos чисел. При этом сколько из них могут быть больше pos. Казалось бы, тоже n - pos, но это не так, так как число n, большее pos, стоит не правее, чем n :). Поэтому, по принципу Дирихле, найдется число, которое меньше или равно pos, и стоит справа от n.
Как теперь реализовать этот алгоритм за O(n2), а не за куб? Вот мы хотим поставить n на свое место. Идем направо указателем, пока не встретим число, меньшее или равное pos, а потом поменяем n с этим числом. Дальше указатель надо пускать уже от новой позиции n, поэтому указатель всегда двигается только вправо, и суммарно пройдет не больше n. Итак, каждое из n чисел мы ставим на свою позицию за O(n), поэтому получаем O(n2).
