Please read the new rule regarding the restriction on the use of AI tools. ×

Hesham.Elkhatib's blog

Wilson's Theorem
By Hesham.Elkhatib, 11 years ago, In English

I Want to know how wilson theorem can be used to efficiently calculate nCr % P where P is prime

and how it can help to solve this Problem

also it will be appreciated to mention some of its applications :)

  • Vote: I like it
  • +6
  • Vote: I do not like it

Comments Comments (13)
| Write comment?
»
11 years ago, # |
← Rev. 2   Vote: I like it +24 Vote: I do not like it

You don't do this using Wilson. Wilson is about , while your factorials are n!, (n - r)!, r!, none of which are in any way related to p.

If p > n, we know that r! and (n - r)! are coprime to p, therefore

by Fermat's little theorem. If $n$ is small enough, you can pre-compute all factorials up to n and the rest is just fast modular exponentiation.

Also, nCr is not a good notation. Try {n \choose r } in : .

Hope this helps in some way.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    I think that the exponent in formula should be p — 2, not p — 1.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Whoops, right. Quickly typed post...

      → Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it +6 Vote: I do not like it

    Well, there's some thing. I think the author may think about the case that n is very large (n > (1LL << 63)) and p is a int or long long type integer. I think there's something that wilson theorem can do. Let x = (n!) / ((n — r)! * r!), the answer.

    First thing to do, we should check if x == 0 by using Lp(n!)=∑[n/p^k] (k>=1). If x != 0, then since n is so large, the we should say n = k*p + b. Then

    n! = 1*2*...*(p — 2)*(p-1)*p*(p + 1)*(p+2)*...*(kp + 1)*(kp+2)*...(kp+b); = 1*2*...*(p -2)*(p — 1)*p*1*2*...*(p — 1)*2p*1*2...*(p — 1)*kp*1*2*...*b; = ((p — 1)!)^k*k!*b! MOD p;

    since k is also very large, we need recursion function to calculate that. b<p, so b! can be calculate in a short time, you can calculate all b! before everything starts. (n — r)! ans r! can be calculate in the same way. The use the quick_power to calculate the reverse. that's ((n-r)!*r!)^(p-2). That's it.:D

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yes, that's another way. I don't see where you use Wilson's theorem, though. And it has the downside of using O(p) time and memory (the memory can be a bigger problem than the time here), which makes it applicable only for really small p.

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it +6 Vote: I do not like it

        n! = 1*2*...*(p-2)*(p-1)*p*(p+1)*(p+2)*...*(kp+1)*(kp+2)*...(kp+b);

        = 1*2*...*(p-2)*(p-1)*p*1*2*...*(p-1)*2p*1*2...*(p-1)*kp*1*2*...*b;

        = ((p-1)!)^k*k!*b! MOD p;

        Using wilson theorem, we know (p-1)! = -1 MOD p; So this part ((p-1)!)^k will always be 1 or -1, depends on k.

        BTW the simplest way to calculate (n-r)!*r! will always cost O(p) time. Any faster way suggested, since you also need to calculate that in your method?

        And in the case that there're large numbers of inputs, I suggest pre-calculate all the b!, most of time we don't need to do that. :D

        → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          Oh, ok. Still, Wilson just removes one line from the code, without improving its actual complexity :D

          I meant that p is mostly large (binomial coefficients usually appear as part of more complex combinatorial problems), so ways with O(n) precalculaton and time per query, or even with a 2D table of coefficients, are much more common. O(p) is almost just for this particular problem (for which tl;dr, I'm just looking at your post below :D).

          → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it +6 Vote: I do not like it

        And I think my way just works fine for the problem the author asked as p < 1000 and n < 10^9 in the statement.

        → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    I just ignore the factor p, since (n-r)!*r! and n! has the same number of factor p in the above case. BTW, recursion's depth won't be too deep(log(n)/log(p)). Otherwise n is so large that it can't be presented in the input. :D

    → Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    N in the problem can be up to 109 . P is only 103 , in the worst case. Lucas theorem is the only way to go.

    → Reply
»
11 years ago, # |
← Rev. 9   Vote: I like it 0 Vote: I do not like it

What you need is not Wilson theorem, you need Lucas theorem :D

This problem is a straightforward problem on Lucas theorem.

Quoted from wikipedia: "

For non-negative integers m and n and a prime p, the following congruence relation holds:

where

and

are the base p expansions of m and n respectively. This uses the convention that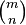 = 0 if m < n.

"

Wikipedia Link

PS: Sorry for the many edits but seems like Codeforces has problems with long LaTex codes!!

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I find YQCMMD's solution above better, because it doesn't rely on Wikipedia (which is not exactly accessible in contests, so it's better not to get too used to it), but can be derived easily. Also, Lucas is overkill here. The simpler, the better.

    → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

really great, thanks all for your beneficial explanations :)

→ Reply