Hi everyone!
Today, I participate in AtCoder contest, which I quite rarely do. Of course, my performance was quite poor, but I stumbled with quite nice idea along the way. To those who didn't read it, the problem goes as follows:
AGC 058 — Yet Another ABC String. How many ternary strings are there such that they contain exactly $$$A$$$ characters a, exactly $$$B$$$ characters b and exactly $$$C$$$ characters c, and do not have any sub-string that is a cyclic shift of abc?
My approach is very different from the one in the editorial, and seems insightful to me, so I decided to share it in detail.
Besides, I can't reject the request by Um_nik to explain it further :D
Walks on finite automata
We may construct a directed graph, such that each edge is marked by a, b or c, and so that the string is valid if and only if there is a walk from the starting vertex so that concatenation of characters on traversed edges form the string. The graph looks like this:
Graph of allowed walks
In the graph with have $$$7$$$ vertices:
- Starting vertex in the middle;
- Vertices $$$a$$$, $$$b$$$ and $$$c$$$ denote the last character and the fact that pre-last character is not important;
- Vertices $$$ab$$$, $$$bc$$$ and $$$ca$$$ denote the last two characters.
As you see, going from $$$ab$$$ by $$$c$$$, from $$$bc$$$ by $$$a$$$ or from $$$ca$$$ by $$$b$$$ is not allowed. The graph may be further simplified to only $$$3$$$ vertices:
Reduced graph of allowed walks
Indeed, we can't traverse from vertices $$$ab$$$, $$$bc$$$ and $$$ca$$$ in one another, so we may as well remove them completely.
Multivariate generating function
Let $$$F(a, b, c)$$$ be the generating function on the number of allowed walks, so that $$$[a^A b^B c^C]F(a, b, c)$$$ is the number of allowed walks that have $$$A$$$ characters a, $$$B$$$ characters b and $$$C$$$ characters c. Then it may be expressed as
where $$$F_a$$$, $$$F_b$$$ and $$$F_c$$$ are the generating functions for walks starting in $$$a$$$, $$$b$$$ and $$$c$$$ correspondingly.
From the graph structure it follows that
Note that this is also one of common approaches to construct a regular expression for given DFA.
This may be expressed as a system of linear equations, and the whole answer is given as
I'll be honest here, I don't exactly know the way to compute it manually, but matrixcalc suggests that the answer is
Note that the computation is not exactly pretty:
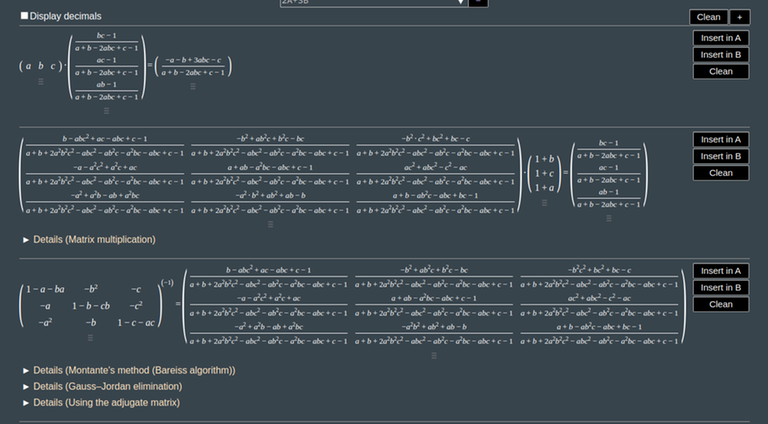
Matrixcalc "suggestion"
Um_nik orz for computing it manually!
What to do with the generating function?
I was hesitant to publish this blog until I got the actual working solution here. Big thanks to Golovanov399 for sharing it!
Well, first of all multiplying both parts by the denominator we get that
where $$$F_0(a, b, c) = 3abc - (a+b+c)$$$ is insignificant to higher terms of $$$F$$$.
From the formula above it follows that
where $$$F[A][B][C] = [a^A b^B c^C]F(a, b, c)$$$ is the answer to the problem. Not exactly the result that is obvious from the statement, is it?
However, the problem requires the solution in $$$O(A+B+C)$$$ and, luckily, it is also possible to find it from the generating function!
Let $$$G(a,b,c) = \frac{1}{a+b+c-2abc-1}$$$. Note that
hence the computation of $$$[a^A b^B c^C] F$$$ can be reduced to $$$4$$$ computations of similar thing in $$$G$$$.
And to compute $$$[a^A b^B c^C] G$$$ you should note that
Among all the terms on the right, only $$$\min(A, B, C)$$$ contribute to $$$[a^A b^B c^C] G$$$ and we may find them all by iterating over $$$l$$$.
Here, $$$\binom{i+j+k+l}{i,j,k,l} = \frac{(i+j+k+l)!}{i!j!k!l!}$$$ is a multinomial coefficient.











You may also like the most recent projecteuler problem