For the largest k=2^29-1, the standard solution (STD) use about 500 vertices, but my solution only use less than 100 vertices (exactly 92).
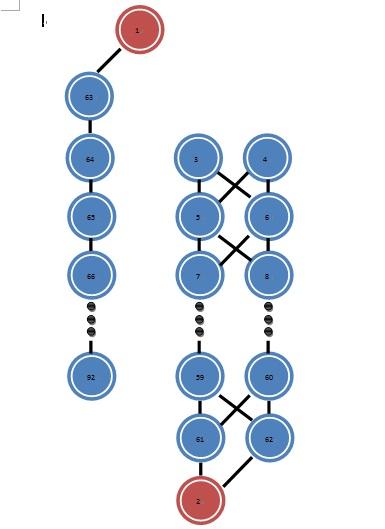
For example, if needs 1 path, add an edge between 61 & 92. if needs 2 paths, add an edge between 59 & 91. More commonly, if needs 2^n paths, add an edge between 61-n*2 & 92-n.
For the input k, transform k to binary type. For example k = 9 = (1001)2. Add edges between 61 & 92, 55 & 88.
You can view my code here 5891486
PS. Taube 5886357 seems to have a better solution for he use less than 90 vertices.










I had the same idea of putting k into binary, and my solution also only uses 100 nodes.
I had the same idea too... But my code's answer has 95 vertexes for every valid test :D
I think that the best solution is your solution, but instead of nesting 2 by 2 nodes, do it 4 by 4.
On the worst case when k=4^9-1 it uses 77 nodes
Submission: 5892749
Firstly I used the same idea (I called it 'two columns') and got n=1036 (!!!), then I use 'four columns ' to reduce n into 660.
I think that we can consider the following idea:
k = a[1]*(b1^b1) + a[2]*(b2^b2) + ...
x^x can be described by a table x*x. Cell[i][j] connects to every Cell[i+1][1..x].
I'm sorry that my bad English couldn't describe this idea better.
awesome solution!
My solution is same.