Note that this Saturday, this year's last (before the Olympiad's Open) round of COCI takes place.

Registration and entry into the contest: here. Watch out — don't register for HONI (local version), but COCI.

Feel free to discuss problems here after the contest ends. I'll probably post my solutions here, too.

The contest is over. The results are accessible in your account on evaluator.hsin.hr under the Results tab. The top 5 are:

1. bmerry
2. andreihh
3. eduardische
4. svanidz1
5. Topi Talvitie

Solutions

(all full, except the last problem; you can find the solution of that problem in the comments)

VJEKO

(code)

Do I even have to write anything? For every word on the input, check if the part of the pattern before the asterisk is its prefix and the part after it is its suffix. If they both are, the answer's yes. Can be implemented more comfortably using the STL substr() function. Any bruteforce works.

FONT

(code)

Assign a bitmask of 26 bits to each word — the i-th bit is 1 iff the i-th letter of the alphabet is present in the string. It's obvious that we're asked to compute sets of words whose bitwise OR is equal to 2²⁶ - 1.

We face 2 difficulties here. First, the time limit is too low for an O(N2^N) solution. We need an O(2^N) one, using something like Gray code. But we can't do a classic Gray code memoization, because we don't have enough memory. We need to find some kind of trick to get a full score. I iterated over all numbers with N - 1 bits (corresponding to subsets of the last N - 1 words) and used the lastone() function from Fenwick trees to always get the last non-zero bit of the number; I remembered the bitmasks of the words corresponding to all bits (in 2 arrays, to save memory; it just adds an if-else condition) and used bitwise magic to make my program faster. When I know the OR value of bitmasks of all words in that subset, I just check separately whether that value's good and whether its OR with the last word's bitmask is good. Time complexity: O(2^N); memory: O(2^N / 2).

The TEST option helps a lot in estimating what's fast enough.

KOCKICE

(code)

We can only choose the middle column's height. Let's say that this height is H; then, the cost for changing the i-th column of array R is , and similarly for array S. So then, let's define a new array A with 2N elements: 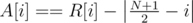, 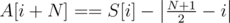and sort it. If we subtracted H from all elements of A (the sorted order of elements remains the same), the result would be the sum of absolute values of all elements of A.

If, after subtracting H > 0 from all elements of A, we got A[N + 1] < 0, then subtracting H - 1 would give us a smaller answer. That's because all absolute values of A[1..N + 1] would decrease and at most N - 1 remaining ones could increase — the answer would decrease by at least 1. The same applies for A[N] > 0 (so A[N + 1] ≥ A[N] > 0) and subtracting H + 1 instead of H ≥ 0.

That means: if A[N + 1] ≤ 0, then H = 0 (H < 0 is digging a hole in the ground...); if A[N + 1] > 0, we want H = A[N + 1]. Pick the right H, subtract and calculate the answer. Time complexity: due to sorting.

KRUZNICE

(code)

This problem would be called the same in Slovak :D

Observe that we don't need whole circles, the intervals that are formed by their intersection (as full circles) with the x-axis are sufficient. That's because the circles can touch only at the x-axis (proof to the reader). Each circle cuts out one new region from the whole plane or a circle that it's inside of; for each circle c, one more region's added if there are two or more smaller circles that form a chain from one to another end of c. In this case, a chain of circles (or intervals) is a sequence of circles that touch (or intervals with a common endpoint). It's obvious that if such a chain exists, the inside of circle c is cut into 2 symmetric halves; otherwise, those 2 halves are connected, because no 2 circles can intersect, and no other regions can be cut out (once again, proof to the reader; during a contest in this case, an insight into this is sufficient and there's no need for solid proofs).

This sounds like a graph with endpoints of intervals being vertices and intervals connecting the endpoints as edges — participants of Codechef Feb Long Challenge would agree :D. A chain in this case is a cycle formed when adding circles (intervals, edges) by increasing radius.

This kind of adding edges sounds a lot like DSU. In fact, you can apply the DSU algorithm (the answer is then N + 1, for each circle plus the region that remains from the initial plane, plus the number of cyclic edges found during DSU), or just realize that the number of cyclic edges is given just by the number of connected components and vertices of the graph.

Time complexity: , if we want to compress the x-coordinates or store them in a map<>.

HASH

(code)

This problem was another pain in the ass when optimizing time and memory. Seriously, was it so hard to use N ≤ 8 or a time limit of 3 seconds?

My solution is a bruteforce using the meet-in-the-middle trick. The point is that we can calculate hashes of the first 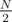letters for all ways of picking those 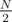letters, and also what those hashes would have to be in order to give K when hashing them with the last 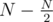letters.

The first bruteforce can be done by remembering hashes in a 2D array: H[i] stores all hashes that we can get with i letters (26ⁱ elements), and we can get the elements of H[i + 1] by iterating over all elements of H[i] and trying to add each of the 26 i + 1-st letters. It's clear that the hash for every word with  ≤ i letters will be computed exactly once and in O(1) time, and the number of those words, and so the time complexity of this part, is .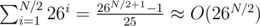

What about the second bruteforce? Xor is its own inverse and 33 is coprime to the modulus, so it has a modular inverse; its value %2^M is I = 33^{φ(2M) - 1} = 33^{2M - 1 - 1}. So if the last letter had an ordinal value of x, then the hash of our word without that letter is ((K^x)·I)%2^M (modulo trashes all but the last M bits, so xor doesn't affect it, and multiplying by modular inverse is an inverse operation to multiplying by 33 %2^M, so it gives us the hash we're looking for by definition). This is almost identical to the first bruteforce, we just start with K instead of 0 and do the operations (xor, multiplication) in reverse order. The time complexity is the same.

How to merge the 2 results? One more array with some 2²⁵ = 3.3·10⁷ elements can still fit into the memory. This array, P, will be the number of occurences of hash P among the first bruteforce's results (the hashes of 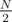elements). Traverse all those hashes H, for each of them increment P[H], then traverse the results of the second bruteforce (the required hashes) and for hash H add P[H] to the answer. Once again, every word with hash K will be counted in the answer exactly once.

Time and space complexity: O(26^N / 2 + 2^M). It actually fits into the limit, if you don't do something stupid like sorting the bruteforces' resulting hashes and using 2 pointers to compute the answer (quicksort is fast, but not fast enough, even if it cuts off the 2^M factor from complexities).

GRASKRIZA

(code)

You can look for an optimal solution in the comments. But let me tell you that a stupid bruteforce (add traffic lights to all grid points of the smallest rectangle bounding the input traffic lights, that are above any already existing traffic light) gives 96 points :D

I tell you, I don't miss the times (first COCI contest of 2013/14) when a solution that was significantly faster than a bruteforce got 30% of the points just like a bruteforce.