Hi Codeforces,
I've tried my best to make a different editorial, I wish you enjoy it ...
problem author: MohammadParsaElahimanesh, AmirrzwM
step 1:
It's obvious that the answer is "NO" if $$$a_{i} = 0$$$ for all $$$1 \le i \le n$$$.
step 2:
Lets prove that the answer is "YES" if $$$a_{i} = 1$$$ for at least one $$$1 \le i \le n$$$.
step 3:
If size of $$$a$$$ is equal to $$$k$$$, just use second type operation once and we are done.
step 4:
Otherwise (if $$$|a| > k$$$), there will be three cases: (assume that $$$a_{j} = 1$$$)
- if $$$j > 2$$$, you can use first type operation on first and second element and decrease size of $$$a$$$ by 1.
- else if $$$j < |a|-1$$$, you can use first type operation on last and second to last element and decrease size of $$$a$$$ by 1.
- else, it can be shown easily that $$$|a| = 3$$$ and $$$k = 2$$$ so you can use second type operation twice and turn $$$a$$$ into a single $$$1$$$.
In first and second case, you can continue decreasing size of $$$a$$$ until $$$|a| = k$$$ (or you reach $$$3$$$-rd case) and you can use second type operation to reach your aim.
step 5:
So we proved that the answer is "YES" iff $$$a_{i} = 1$$$ for at least one $$$1 \le i \le n$$$ or in other words, iff $$$\sum_{i = 1}^n a_{i} > 0$$$.
// In the name of God
#include <iostream>
using namespace std;
int main()
{
int t;
cin >> t;
while(t--)
{
int n, k;
cin >> n >> k;
int sum = 0;
for(int i = 0 ; i < n ; i++){
int a;
cin >> a;
sum += a;
}
if(sum > 0) cout << "YES" << endl;
else cout << "NO" << endl;
}
return 0;
}
// Thank God
problem author: MohammadParsaElahimanesh
step 1:
Assume that $$$a_{i} = 0$$$ for each $$$1 \le i \le n$$$, what should we do?
Nothing! The array is already sorted and the answer is $$$0$$$.
step 2:
After sorting the array, consider the first non-zero element of $$$a$$$, how many elements after that are equal to zero? In other words, consider smallest $$$i$$$ such that $$$a_{i} > 0$$$, how many indices $$$k$$$ exist such that $$$i < k$$$ and $$$a_{k} = 0$$$?
0, because we call an array $$$a$$$ sorted (in non-decreasing order), if for all $$$1 \le i < j \le n$$$, $$$a_{i} \le a_{j}$$$ holds. So all numbers after leftmost non-zero element must be non-zero too.
step 3:
assume that after sorting $$$a$$$, $$$a_{i}$$$ ($$$1 \le i \le n$$$) is the leftmost non-zero element. Define $$$G_{1}$$$ as the set of indices $$$j$$$ such that $$$1 \le j < i$$$ and $$$a_{j} > 0$$$ at the beginning, also define $$$G_{2}$$$ as the set of indices $$$j$$$ such that $$$i \le j \le n$$$ and $$$a_{j} = 0$$$ at the beginning. What is the answer?
$$$max(|G_{1}|, |G_{2}|)$$$. It's obvious that in one operation at most one element will be deleted from each group. So we must perform at least $$$max(|G_{1}|, |G_{2}|)$$$ operations. Now we want to show that it's sufficient too. There are three cases:
$$$min(|G_{1}|, |G_{2}|) > 1$$$, at this point, we know that all elements of $$$a$$$ are $$$0$$$ or $$$1$$$. So we can pick one element from $$$G_{1}$$$ and add it to an element from $$$G_{2}$$$, so the size of both groups will decrease by $$$1$$$. It's obvious that all elements of $$$a$$$ will remain less than or equal to $$$1$$$ after this operation.
$$$|G_{1}| = 0$$$, it's easy to see that we can add $$$a[k]$$$ ($$$k \in G_{2}$$$) to a random element. So $$$|G_{2}|$$$ will decrease by $$$1$$$.
$$$|G_{2}| = 0$$$, it's easy to see that we can add $$$a[k]$$$ ($$$k \in G_{1}$$$) to the last element of $$$a$$$. So $$$|G_{1}|$$$ will decrease by $$$1$$$.
step 4:
Now how can we solve the problem using previous steps?
If all elements are equal to $$$0$$$, the answer is obviously zero. Otherwise we will calculate two arrays, number of ones in each prefix and number of zeros in each suffix. We will also fix the leftmost non-zero element and calculate the answer for it easily by using Step 3 algorithm in O(n).
/// In the name of God
#include <iostream>
using namespace std;
int main()
{
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
int A[n], cnt[2][n+1];
cnt[0][0] = cnt[1][0] = 0;
for(int i = 0; i < n; i++)
{
cin >> A[i];
cnt[0][i+1] = cnt[0][i]+(A[i]==0?1:0);
cnt[1][i+1] = cnt[1][i]+(A[i]==1?1:0);
}
int ans = n-1;
for(int last_zero = 0; last_zero <= n; last_zero++)
ans= min(ans, max(cnt[1][last_zero], cnt[0][n]-cnt[0][last_zero]));
cout << ans << endl;
}
}
/// Thank God . . .
1746C - Permutation Operations
problem author: napstablook
step 1:
Try to prove that the answer is always zero. Or in other words, we can always make the array $$$a$$$ non-decreasing.
We will prove this fact in next steps.
step 2:
If some array $$$a$$$ is non-decreasing, what can we say about array $$$d=[a_{2}-a_{1}, a_{3}-a_{2}, ... a_{n}-a_{n-1}]$$$?
It's obvious that all elements of array $$$d$$$ should be non-negative.
step 3:
If we perform the $$$i$$$-th operation on the suffix starting at index $$$j$$$, what happens to array $$$d$$$?
All elements of it will remain the same except $$$d_{j-1}=a_{j}-a_{j-1}$$$ which will increase by $$$i$$$.
step 4:
Considering the fact that array $$$a$$$ consists only of positive integers, what can we say about $$$d_{i}=a_{i+1}-a_{i}$$$?
Since $$$a_{i+1} \ge 0$$$, we can say that $$$d_{i} \ge -a_{i}$$$.
step 5:
Using step 3 and 4 and knowing that $$$a$$$ is a permutation of numbers $$$1$$$ to $$$n$$$, what can we do to make all elements of $$$d$$$ non-negative?
for $$$i \le n-1$$$, we can perform $$$a_{i}$$$-th operation on the suffix starting from index $$$i+1$$$. So $$$d_{i}$$$ will increase by $$$a_{i}$$$ and since we knew that $$$d_{i} \ge -a_{i}$$$, after performing this operation $$$d_{i} \ge 0$$$ will hold. So after this steps, elements of $$$d$$$ will be non-negative and according to Step 2, that's exactly what we want. It's also easy to see that it doesn't matter how we perform $$$a_{n}$$$-th operation, so we can do anything we want.
/// In the name of God
#include <bits/stdc++.h>
using namespace std;
inline void solve()
{
int n;
cin >> n;
int permutation[n], location[n];
for(int i = 0; i < n; i++)
{
cin >> permutation[i];
permutation[i]--;
location[permutation[i]] = i;
}
for(int i = 0; i < n; i++)
{
if(location[i] == n-1)
cout << rand()%n+1 << (i == n-1?'\n':' ');
else
cout << location[i]+2 << (i == n-1?'\n':' ');
}
}
int main()
{
int t;
cin >> t;
while(t--)
solve();
return 0;
}
/// Thank God . . .
problem author: AquaMoon, Cirno_9baka, mejiamejia, ChthollyNotaSeniorious, SSerxhs, TomiokapEace
Define $$$f(u, cnt)$$$ represents the maximum score of $$$cnt$$$ balls passing through the subtree of node $$$u$$$.
Define $$$num$$$ as the number of the sons of node $$$u$$$. The transition is only related to $$$\lceil cnt / num \rceil$$$ and $$$\lfloor cnt / num \rfloor$$$ two states of the subtree.
For each node $$$u$$$, $$$cnt$$$ can only be two adjacent integer $$$(x, x + 1)$$$.
It can be proved that the four numbers $$$\lfloor x/num \rfloor$$$, $$$\lceil x/num \rceil$$$, $$$\lceil (x + 1)/num \rceil$$$ and $$$\lfloor (x + 1)/num \rfloor$$$ can only have two kinds of numbers at most, and they are adjacent natural numbers.
So the number of states can be proved to be $$$\mathcal{O}(n)$$$.
/// In the name of God
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200000;
ll V[N], dp[N];
int dad[N];
vector<int> child[N];
vector<pair<int, ll>> answers[N];
inline ll DP(int v, ll k)
{
for(auto [kp, ans]: answers[v])
if(k == kp)
return ans;
ll cnt_child = (ll)child[v].size();
ll ans = k*V[v];
if(cnt_child == 0)
return ans;
if(k%cnt_child == 0)
for(auto u: child[v])
ans += DP(u, k/cnt_child);
else
{
ll dp1[cnt_child], dp2[cnt_child], diff[cnt_child];
for(int i = 0; i < cnt_child; i++)
dp1[i] = DP(child[v][i], k/cnt_child), dp2[i] = DP(child[v][i], k/cnt_child+1);
for(int i = 0; i < cnt_child; i++)
diff[i] = dp2[i] - dp1[i];
sort(diff, diff+cnt_child, greater<int>());
for(int i = 0; i < cnt_child; i++)
ans += dp1[i];
for(int i = 0; i < k%cnt_child; i++)
ans += diff[i];
}
answers[v].push_back({k, ans});
return ans;
}
inline ll solve()
{
ll n, k;
cin >> n >> k;
for(int i = 0; i < n; i++)
child[i].clear(), answers[i].clear();
dad[0] = 0;
for(int i = 0; i < n-1; i++)
{
cin >> dad[i+1];
dad[i+1]--;
child[dad[i+1]].push_back(i+1);
}
for(int i = 0; i < n; i++)
cin >> V[i];
return DP(0, k);
}
int main()
{
int t;
cin >> t;
while(t--)
cout << solve() << '\n';
return 0;
}
/// Thank God . . .
1746E1 - Joking (Easy Version)
problem author: MohammadParsaElahimanesh
step 1:
How can we make sure that some statement is not joking?
If something is told for two times in a row, we can be sure that it's true. For example if we are told that $$$x \ne 3$$$ in two consecutive questions, we can be sure that it's true. Because at least one of those questions is answered correctly and that's enough.
step 2:
What can be found out if we ask about a set $$$S$$$? (assume that we will be answered correctly)
If the answer is "YES", then $$$x \in S$$$ and we can reduce our search domain to $$$S$$$. Otherwise, we can remove $$$S$$$ from the search domain.
step 3:
Using previous steps, how can we really reduce our search domain? Step 2 can do it only if we have a correct statement about $$$x$$$ and using Step 1, we can find something that is surely correct.
Assume that $$$V$$$ is our current search domain. Split it into $$$4$$$ subsets $$$V_{1}, V_{2}, V_{3}$$$ and $$$V_{4}$$$. then ask about following sets:
- $$$V_{1} \cup V_{2}$$$
- $$$V_{1} \cup V_{3}$$$
It's easy to show that no matter what the answers are, we can always remove at least one of the subsets from the search domain. For example if both answers are "YES", we can remove $$$V_{4}$$$ and if both answers are "NO", then we can remove $$$V_{1}$$$.
So after these questions, we can reduce size of search domain by at least $$$min(|V_{1}|,|V_{2}|,|V_{3}|,|V_{4}|)$$$, and it's obvious to see that we can choose $$$V_{i}$$$'s in such a way that this value is at least $$$\frac{|V|}{4}$$$.
Finally, as long as size of the search domain is greater than $$$3$$$, we can reduce it using this algorithm. It can be shown easily that we can reduce our search domain to only $$$3$$$ numbers with at most $$$76$$$ questions.
step 4:
Now assume that we have only $$$3$$$ candidates for $$$x$$$, since we have only $$$2$$$ chances to guess, we must remove one of them. How can we do it? Note that since we've used $$$76$$$ questions in previous step, we only have $$$6$$$ questions left.
Assume that our three candidates are $$$a, b$$$ and $$$c$$$. it can be shown that using following questions, we can always remove at least one of them from the search domain:
- $$${a}$$$
- $$${b}$$$
- $$${b}$$$
- $$${a}$$$
After that, when we have only two candidates for $$$x$$$, we can guess them one by one and we are done.
/// In the name of God
#pragma GCC optimize("Ofast","unroll-loops","O3")
#include <bits/stdc++.h>
using namespace std;
inline bool get_answer(){string s; cin >> s; return s == "YES";}
inline bool f(int i){return i&1;}
inline bool g(int i){return i&2;}
void solve(const vector<int> &Valid)
{
if(Valid.size() < 3u)
{
cout << "! " << Valid[0] << endl;
string s;
cin >> s;
if(s == ":)")return;
cout << "! " << Valid[1] << endl;
return;
}
else if(Valid.size() == 3u)
{
bool is[4];
cout << "? 1 " << Valid[0] << endl;is[0] = get_answer();
cout << "? 1 " << Valid[1] << endl;is[1] = get_answer();
cout << "? 1 " << Valid[1] << endl;is[2] = get_answer();
cout << "? 1 " << Valid[0] << endl;is[3] = get_answer();
if(is[1] and is[2])return solve({Valid[1]});
else if(!is[1] and !is[2])return solve({Valid[0], Valid[2]});
else if((is[0] and is[1]) or (is[2] and is[3]))return solve({Valid[0], Valid[1]});
else if((is[0] and !is[1]) or (!is[2] and is[3]))return solve({Valid[0], Valid[2]});
else return solve({Valid[1], Valid[2]});
}
else
{
vector<int> query[2];
for(int i = 0; i < (int)Valid.size(); i++)
{
if(f(i))query[0].push_back(Valid[i]);
if(g(i))query[1].push_back(Valid[i]);
}
bool is[2];
for(int i = 0; i < 2; i++)
{
cout << "? " << query[i].size();
for(auto u: query[i])cout << ' ' << u;
cout << endl;
is[i] = get_answer();
}
vector<int> NewValid;
for(int i = 0; i < (int)Valid.size(); i++)
{
if((!f(i) ^ is[0]) or (!g(i) ^ is[1]))NewValid.push_back(Valid[i]);
}
return solve(NewValid);
}
}
int main()
{
int n = 0;
cin >> n;
vector<int> all(n);
for(int i = 0; i < n; i++)all[i] = i+1;
solve(all);
return 0;
}
/// Thank God . . .
1746E2 - Joking (Hard Version)
problem author: MohammadParsaElahimanesh, AmirrzwM
step 1:
First note that in any question we ask, a set will be introduced as the set that contains $$$x$$$. If the answer is "YES", then the set that we asked is introduced and otherwise, its complement.
Assume that our current search domain is some set $$$V$$$. In addition, assume that $$$V = A \cup B$$$ such that set $$$A$$$ is the set that introduced to contain $$$x$$$ in very last step and $$$B$$$ is the set of other candidates for $$$x$$$ (candidates that don't belong to $$$A$$$). Now assume that in next question, a set $$$C$$$ is introduced to contain $$$x$$$ such that $$$C = a \cup b, (a \in A , b \in B)$$$. what can we do? how can we reduce our search domain after this question?
Considering the solution of E1, it's not so hard to see that we can remove $$$B-b$$$ from our search domain. So our new search domain will be $$$V' = A' \cup B'$$$ such that $$$A' = C = a \cup b$$$ is the set of candidates that introduced in last question and $$$B' = A - a$$$ is the set of other candidates.
step 2:
Let's calculate minimum needed questions for a search domain of size $$$n$$$ using the idea of previous step.
We can do it using a simple dp, let $$$dp[A][B]$$$ be the minimum number of questions needed to find $$$x$$$ in a search domain of size $$$A+B$$$ in which $$$A$$$ numbers are introduced in last question and $$$B$$$ numbers are not. In order to calculate our dp, if we ask about some set which consists of $$$a$$$ numbers from first set and $$$b$$$ numbers from second set, we should update $$$dp[A][B]$$$ from $$$dp[A-a][a+b]$$$. So we can say that:
. Using this dp and keeping track of its updates, we can simply solve the task. But there is a problem, we don't have enough time to calculate the whole dp. So what can we do?
step 3:
Since calculating $$$dp[A][B]$$$ for $$$A <= n , B <= m$$$ is $$$O(n^2 \cdot m^2)$$$, we can only calculate it for small $$$n$$$ and $$$m$$$ like $$$n,m \le 100$$$. What can we do for the rest? Maybe some heuristic method?
It's not so hard to see that for most $$$A$$$ and $$$B$$$ (especially for large values) it's best to update $$$dp[A][B]$$$ from something around $$$dp[A-A/2][A/2+B/2]$$$ (in other words, asking $$$A/2$$$ numbers from the first set and $$$B/2$$$ numbers from the second one). Using such method, we can calculate dp in a reasonable time and with a very good accuracy, and this accuracy is enough to find the answer in less than $$$53$$$ questions.
/// In the name of God
#pragma GCC optimize("Ofast","unroll-loops","O3")
#include <bits/stdc++.h>
using namespace std;
const int SUM = 50;
int dp[SUM][SUM];
pair<int,int> updater[SUM][SUM];
map<pair<int,int>, int> Dp;
map<pair<int,int>, pair<int,int>> Updater;
inline void preprocess()
{
for(int i = 0; i < SUM; i++)
{
for(int j = 0; j < SUM; j++)
{
dp[i][j] = SUM;
updater[i][j] = {i, j};
}
}
dp[0][0] = dp[0][1] = dp[1][0] = dp[2][0] = dp[1][1] = dp[0][2] = 0;
for(int sum = 0; sum < SUM; sum ++)for(int last = sum; last >= 0; last--)
{
int now = sum - last;
for(int SelectLast = 0; SelectLast <= last; SelectLast++)for(int SelectNow = 0; SelectNow <= now; SelectNow++)
{
if(dp[last][now] > 1 + max(dp[now-SelectNow][SelectNow+SelectLast], dp[SelectNow][sum-SelectNow-SelectLast]))
{
dp[last][now] = 1 + max(dp[now-SelectNow][SelectNow+SelectLast], dp[SelectNow][now+last-SelectNow-SelectLast]);
updater[last][now] = {SelectLast, SelectNow};
}
}
}
}
inline int DP(const int last, const int now)
{
if(last < 0 || now < 0)return SUM;
if(last + now < SUM)return dp[last][now];
if(Dp.find({last, now}) != Dp.end())return Dp[{last, now}];
if((last&1) && (now&1))
{
Dp[{last, now}] = 1 + DP((now+1)/2, (last+ now)/2);
Updater[{last, now}] = {(last+1)/2, now/2};
}
else
{
Dp[{last, now}] = 1 + DP((now+1)/2, (last+1)/2+(now+1)/2);
Updater[{last, now}] = {(last+1)/2, (now+1)/2};
}
return Dp[{last, now}];
}
inline bool IsIn(const int x, const vector<int> &Sorted)
{
auto u = lower_bound(Sorted.begin(), Sorted.end(), x);
if(u == Sorted.end() or *u != x)return false;
return true;
}
vector<int> solve(const vector<int> &LastAns, const vector<int> &Valid)
{
if((int)Valid.size() < 3)
{
return Valid;
}
pair<int,int> Select;
if((int)Valid.size() < SUM)
{
Select = updater[LastAns.size()][Valid.size()-LastAns.size()];
}
else
{
DP((int)LastAns.size(), (int)(Valid.size()-LastAns.size()));
Select = Updater[{LastAns.size(), Valid.size()-LastAns.size()}];
}
vector<int> query;
int p = 0;
while(Select.first --)query.push_back(LastAns[p++]);
p = 0;
vector<int> LastAnsSorted = LastAns;
sort(LastAnsSorted.begin(), LastAnsSorted.end());
while(Select.second --)
{
while(IsIn(Valid[p], LastAnsSorted)) p++;
query.push_back(Valid[p++]);
}
cout << "? " << query.size();
for(auto u: query)cout << ' ' << u;
cout << endl;
string s;
cin >> s;
bool correct = (s == "YES");
sort(query.begin(), query.end());
vector<int> NewLast, NewValid;
for(auto u: Valid)
{
if(!IsIn(u, LastAnsSorted) and (correct ^ IsIn(u, query)))
{
NewLast.push_back(u);
}
if(!IsIn(u, LastAnsSorted) or !(correct ^ IsIn(u, query)))
{
NewValid.push_back(u);
}
}
vector<int> ans = solve(NewLast, NewValid);
return ans;
}
int main()
{
preprocess();
int n;
cin >> n;
vector<int> all(n);
for(int i = 0; i < n; i++)all[i] = i+1;
vector<int> valid = solve({}, all);
for(auto guess: valid)
{
cout << "! " << guess << endl;
string s;
cin >> s;
if(s == ":)")return 0;
}
return 0;
}
/// Thank God . . .
problem author: MohammadParsaElahimanesh
step 1:
First of all, we can compress $$$a_{i}$$$'s and $$$x$$$'s (in second type query). so we can assume that all numbers are less than $$$n+q \le 6 \cdot 10^5$$$.
step 2:
Lets first solve the problem for smaller constrains.
We can use data structures like fenwick tree or segment tree to count the number of occurrences of each number and check if it's divisible by $$$k$$$ to answer second type query. And we can simply update our data structure after each query of the first type.
So if we use something like fenwick tree, we can handle everything in $$$O((n+q) \cdot n + (n+q) \cdot q \cdot log_{2}(n))$$$.
step 3:
Obviously we can not use previous step solution for original constrains. In other words, we don't have enough time to check all numbers one by one. How can we do better? Checking them together?!
It's obviously not a good idea to check all numbers together (checking that sum of their occurrences is divisible by $$$k$$$). So what can we do? What if we check a random subset of numbers?
step 4:
Assume that $$$S$$$ is a random subset of all numbers, it's obvious that if the answer of the query is "YES" (number of occurrences of every number is divisible by $$$k$$$), the condition holds for $$$S$$$ too (sum of number of occurrences of numbers that belong to $$$S$$$ is divisible by $$$k$$$). What about the opposite? What is the probability that the answer of the query is "NO" and yet sum of occurrences of numbers belonging to $$$S$$$ is divisible by $$$k$$$?
It's not so hard to prove that the probability is equal to $$$\frac{1}{2}$$$ for $$$k = 2$$$ and it's less than $$$\frac{1}{2}$$$ for $$$k \ge 2$$$. So in general, the probability that a random subset $$$S$$$ leads to a wrong answer is less than or equal to $$$\frac{1}{2}$$$. So if we use something like $$$30$$$ random subsets, the probability will be less than $$$\frac{1}{2^{30}}$$$ which is reasonable for problem constrains and we can use this random method to solve the task.
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
mt19937 rnd(time(0));
const int N = 300'000 + 5;
const int Q = 300'000 + 5;
const int T = 50;
bitset<N+Q> RandomSet[T];
unordered_map<int, int> id; int cnt_id = 0;
int n, q, A[N];
struct fenwick
{
int PartialSum[N];
fenwick()
{
for(int i = 0; i < N; i++)PartialSum[i] = 0;
}
inline void add(int index, bool increase)
{
while(index < N)
{
PartialSum[index] += (increase? 1 : -1);
index += index&-index;
}
}
inline int get(int index)
{
int sum = 0;
while(index)
{
sum += PartialSum[index];
index -= index&-index;
}
return sum;
}
}Fen[T];
inline int GetId(const int x)
{
auto id_iterator = id.find(x);
if(id_iterator == id.end())
{
return id[x] = cnt_id++;
}
else return (*id_iterator).second;
}
inline void ChooseRandomSets()
{
for(int i = 0; i < T; i++)
{
for(int j = 0; j < N+Q; j++)
{
if(rnd()&1)RandomSet[i].set(j);
}
}
}
inline void AddArrayToFenwick()
{
for(int i = 0; i < n; i++)
{
int MyId = GetId(A[i]);
for(int j = 0; j < T; j++)
{
if(RandomSet[j][MyId])Fen[j].add(i+1, true);
}
}
}
inline void Query()
{
int index, l, r, k, x, type;
for(int i = 0; i < q; i++)
{
cin >> type;
if(type == 1)
{
cin >> index >> x;
index --;
int IdPre = GetId(A[index]);
int IdNew = GetId(x);
A[index] = x;
for(int j = 0; j < T; j++)
{
if(RandomSet[j][IdPre])Fen[j].add(index+1, false);
if(RandomSet[j][IdNew])Fen[j].add(index+1, true);
}
}
if(type == 2)
{
cin >> l >> r >> k;
l--;
if(k == 1){cout << "YES\n"; continue;}
else if((r-l)%k != 0){cout << "NO\n"; continue;}
bool answer = true;
for(int j = 0; j < T; j++)
{
if((Fen[j].get(r)-Fen[j].get(l))%k != 0){answer = false; break;}
}
cout << (answer?"YES":"NO") << '\n';
}
}
}
int main()
{
ios::sync_with_stdio(false) , cin.tie(0);
ChooseRandomSets();
cin >> n >> q;
for(int i = 0; i < n; i++) cin >> A[i];
AddArrayToFenwick();
Query();
return 0;
}
problem idea: SirShokoladina
problem development: SomethingNew, pakhomovee, SirShokoladina
Consider all subsets of the original set in which tasks can be performed in some order to satisfy the constraints on their completion, and also that the size of each of them does not exceed $$$a+b+c$$$. It is easy to show that this set is a weighted matroid. This means that the optimal set of tasks can be found using a greedy algorithm.
So, we can find a set of tasks with maximum total usefulness, which:
- satisfies all deadline constraints
- has no more than $$$a+b+c$$$ elements
For the given parameters $$$(x, y, z)$$$, we introduce the following transformation:
- Increase the usefulness of all tasks of the first type by $$$x$$$, the second type~--- by $$$y$$$, and the third type~--- by $$$z$$$.
Let's assume that the optimal solution after the transformation is described by the triple $$$[a',b',c']$$$~--- the number of problems of each type, respectively. We need to get a solution described by the triple $$$[a,b,c]$$$. For $$$[a,b,c] \neq [a',b',c']$$$, $$$a+b+c=a'+b'+c'$$$ holds. Then (without limitation of generality, since there are at least two inequalities among $$$a\vee a',b\vee b',c\vee c'$$$) we assume that $$$a'>a,b'<b$$$.
Consider the following coordinate system on a two-dimensional plane (modulo the addition of $$$\overrightarrow{(1;1;1)})$$$:
For the coordinates of the point, we take the value $$$\vec{x}\times x+\vec{y}\times y + \vec{z}\times z$$$$$$(\vec{x}+\vec{y}+\vec{z} =\vec{0})$$$. It is easy to understand that the coordinates of the point $$$(x; y)$$$ on the plane are uniquely set by the triple $$$(x; y; z)$$$ up to the addition of $$$\overrightarrow{(1;1;1)} \times k, k \in\mathbb{Z}$$$
Let's assume that there are parameters $$$(x,y,z)$$$ for which the optimal solution is unique and equal to $$$[a,b,c]$$$ (see "But what if..?" to see what needs to be done to the input to make this hold).
Consider the solution $$$[a',b',c']$$$ for the "center" of the current polygon (initially it is a hexagon with infinitely distant coordinates). The "center" is the center of the triangle formed by the middle lines of our polygon.
On this plane, decreasing $$$z$$$ or $$$y$$$ does not increase $$$b'+c'$$$, therefore, it does not decrease $$$a'$$$. Thus, the red area in the picture below does not suit us.
Increasing $$$x$$$ or $$$z$$$ does not decrease $$$a'+c'$$$, therefore, it does not increase $$$b'$$$. Because of this, the blue area in the picture below does not suit us either.
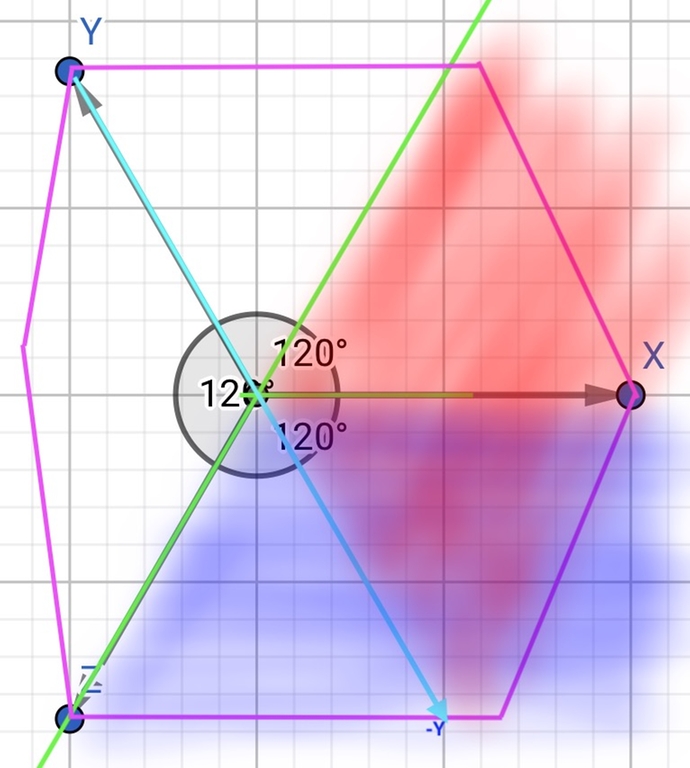
So, we need to cut off one half-plane along the $$$z$$$ axis. It can be shown that the area of the polygon under consideration decreases by a constant time for every 2-3 iterations.
But what if the number of tasks of the desired color jumps from $$$a-1$$$ to $$$a+1$$$ at once? This is possible if and only if with the addition of some $$$x$$$ we get several pairs of elements of equal weight at the same time. To get rid of this, we can simply add a random number from $$$0$$$ to $$$\frac{1}{3}$$$ to each weight. The fact that such a change will fix the problem described above and will not change the optimal answer to the original problem remains to the reader as an exercise (the authors have proof).
After $$$O(\log C)$$$ iterations, our algorithm will converge to a point (a triple of real numbers). It remains only to check that the solution found is suitable for us.
$$$O(n\log n\log C)$$$
#include <bits/stdc++.h>
using namespace std;
#ifdef SG
#include <debug.h>
#else
template<typename T> struct outputer;
struct outputable {};
#define PRINT(...)
#define OUTPUT(...)
#define show(...)
#define debug(...)
#define deepen(...)
#define timer(...)
#define fbegin(...)
#define fend
#define pbegin(...)
#define pend
#endif
#define ARG4(_1,_2,_3,_4,...) _4
#define forn3(i,l,r) for (int i = int(l); i < int(r); ++i)
#define forn2(i,n) forn3 (i, 0, n)
#define forn(...) ARG4(__VA_ARGS__, forn3, forn2) (__VA_ARGS__)
#define ford3(i,l,r) for (int i = int(r) - 1; i >= int(l); --i)
#define ford2(i,n) ford3 (i, 0, n)
#define ford(...) ARG4(__VA_ARGS__, ford3, ford2) (__VA_ARGS__)
#define ve vector
#define pa pair
#define tu tuple
#define mp make_pair
#define mt make_tuple
#define pb emplace_back
#define fs first
#define sc second
#define all(a) (a).begin(), (a).end()
#define sz(a) ((int)(a).size())
typedef long double ld;
typedef signed __int128 lll;
typedef unsigned __int128 ulll;
typedef int64_t ll;
typedef uint64_t ull;
typedef uint32_t ui;
typedef uint16_t us;
typedef uint8_t uc;
typedef pa<int, int> pii;
typedef pa<int, ll> pil;
typedef pa<ll, int> pli;
typedef pa<ll, ll> pll;
typedef ve<int> vi;
template<typename T> inline auto sqr (T x) -> decltype(x * x) {return x * x;}
template<typename T1, typename T2> inline bool umx (T1& a, T2 b) {if (a < b) {a = b; return 1;} return 0;}
template<typename T1, typename T2> inline bool umn (T1& a, T2 b) {if (b < a) {a = b; return 1;} return 0;}
const int N = 100000;
const int X = 1000000000;
const int T = 3;
struct Input {
int n;
std::array<int, T> k;
int a[N], t[N], d[N];
bool read() {
if (!(cin >> n)) {
return 0;
}
forn (i, T) {
cin >> k[i];
}
forn (i, n) {
cin >> a[i] >> t[i] >> d[i];
--t[i];
--d[i];
}
return 1;
}
void init(const Input& input) {
*this = input;
}
};
struct Data: Input {
ll ans;
void write() {
cout << ans << endl;
}
};
namespace Main {
const lll P = 2 * N + 1;
const lll Q = 2 * N + 2;
const lll R = 2 * N + 3;
const lll A[3] = {3 * P * Q, 3 * P * R, 3 * Q * R};
const lll M = 3 * P * Q * R * N;
const lll inf = (X + 1) * M;
struct SNM {
int rnd = 0;
int n;
int pr[N];
void init(int cnt) {
n = cnt;
forn (i, n) {
pr[i] = i;
}
}
int get_p(int v) {
if (v < 0 || pr[v] == v) {
return v;
}
return pr[v] = get_p(pr[v]);
}
bool add(int v) {
v = get_p(v);
if (v == -1) {
return 0;
}
pr[v] = v - 1;
return 1;
}
};
struct Solution: Data {
SNM snm;
int m;
lll b[N], c[N];
vi ord[T];
array<int, T> check(const array<lll, T>& adds) {
forn (i, n) {
c[i] = b[i] + adds[t[i]];
}
auto cmp = [&](int lhs, int rhs) {
return c[lhs] > c[rhs];
};
static vi q;
q.clear();
forn (i, T) {
static vi w;
w.resize(sz(q) + sz(ord[i]));
merge(all(q), all(ord[i]), w.begin(), cmp);
q.swap(w);
}
snm.init(n);
array<int, T> cnt{};
int tot = 0;
ll val = 0;
for (int i : q) {
if (tot >= m) {
break;
}
if (snm.add(d[i])) {
cnt[t[i]]++;
tot++;
val += a[i];
}
}
if (cnt == k) {
ans = val;
}
return cnt;
}
// x[i] == adds[(i + 1) % T] - adds[i]
array<lll, T> get_middle_point(const array<lll, T>& lb, const array<lll, T>& rb) {
array<lll, T> x;
forn (i, T) {
x[i] = lb[i] + rb[i];
}
lll sum = accumulate(all(x), lll(0));
forn (i, T) {
x[i] = T * x[i] - sum;
if (x[i] >= 0) {
x[i] /= (2 * T);
} else {
x[i] = (x[i] - 2 * T + 1) / (2 * T);
}
}
sum = accumulate(all(x), lll(0));
forn (i, T) {
if (sum < 0 && x[i] < rb[i]) {
x[i]++;
sum++;
}
assert(x[i] >= lb[i]);
assert(x[i] <= rb[i]);
}
assert(sum == 0);
return x;
}
bool search() {
array<lll, T> lb, rb;
forn (i, T) {
lb[i] = -2 * inf;
rb[i] = 2 * inf;
}
while (true) {
{
lll sum_l = accumulate(all(lb), lll(0));
lll sum_r = accumulate(all(rb), lll(0));
forn (i, T) {
lll sol = sum_l - lb[i];
lll sor = sum_r - rb[i];
umx(lb[i], -sor);
umn(rb[i], -sol);
if (lb[i] > rb[i]) {
return 0;
}
}
}
array<lll, T> x = get_middle_point(lb, rb);
array<lll, T> adds{};
forn (i, T - 1) {
adds[i + 1] = adds[i] + x[i];
}
array<int, T> cnt = check(adds);
assert(accumulate(all(cnt), 0) == m);
if (cnt == k) {
return 1;
}
forn (i, T) {
lll d1 = cnt[i] - k[i];
lll d2 = cnt[(i + 1) % T] - k[(i + 1) % T];
if (d1 > 0 && d2 < 0) {
lb[i] = x[i] + 1;
}
if (d1 < 0 && d2 > 0) {
rb[i] = x[i] - 1;
}
}
}
}
void solve() {
forn (i, n) {
b[i] = a[i] * M + i * A[t[i]];
}
forn (i, n) {
ord[t[i]].pb(i);
}
forn (i, T) {
sort(all(ord[i]), [&](int lhs, int rhs) {
return b[lhs] > b[rhs];
});
}
m = accumulate(all(k), 0);
{
array<int, T> r = check({});
if (accumulate(all(r), 0) != m) {
ans = -1;
return;
}
}
forn (i, T) {
array<lll, T> adds{};
adds[i] = inf;
if (check(adds)[i] < k[i]) {
ans = -1;
return;
}
adds[i] = -inf;
if (check(adds)[i] > k[i]) {
ans = -1;
return;
}
}
assert(search());
}
void clear() {
forn (i, T) {
ord[i].clear();
}
}
};
}
Main::Solution sol;
int main() {
#ifdef SG
freopen((problemname + ".in").c_str(), "r", stdin);
// freopen((problemname + ".out").c_str(), "w", stdout);
#endif
int t;
cin >> t;
forn (i, t) {
sol.read();
sol.solve();
sol.write();
sol.clear();
}
return 0;
}











Nice Editorial!
Can someone please explain what is meant by balls passing through the subtree of node u in D Editorial
each path can be assumed as unique balls. Initially we start with k balls(paths) from the root, then at every instant we proceed to some child with a path, that is same as giving that ball to the child.
Can someone explain problem c in a different way? I don't understand what to do after computing the difference array.
suppose that i-th number is x. so now if I add x to all the numbers to the right of x ,then all the numbers on right of x will become greater than x,so inversion due to x will remain in this new array; If I do it with every element of the array then there will be no inversions left.
Here is another approach: https://codeforces.net/blog/entry/107978?#comment-963589
https://codeforces.net/contest/1746/submission/176334148 (skip to the main function)
We will Divide the array into continues sub segment where every sub segment is increasing and we aim to make the array increasing because in this way we will have 0 inversion e.g. 1 6 2 5 3 4 We will Divide to 1 6 2 5 3 4 Now because its add so the order doesn't matter How to make it increasing if we add 6 after 6 we will guarantee that every number after 6 is greater than 6 and go to the next sub segment and add 5 after 5 and so on So the answer will be 1 1 1 1 5 3 For suffix ones I don't care because it will keep the order the same That its my solution i think it is intuitive
I didn't realize that it was a permutation. :((( Thanks for the help
An observation that could be made in any array is that if I try to remove/solve an inversion, it cannot affect the other inversions present in the array. eg. take array as 2 3 4 7 8 6 5 1. we have a(8,6) b(6,5) and c(5,1) as inversions.
Let us first solve inversion b. So we don't touch 6 and add (1+2) to suffix at position 7.
Now since we didn't touch 6, the difference b/w 8 and 6 remains the same.
Also since we are applying operation to the whole suffix, the same amount will be added to both 5 and 1 . So the difference b/w them also remains the same.
Hence we can greedily pick inversions which have smaller difference which can help us to solve the maximum of them.
can you explain how you add (1+2) to suffix at position 7?
For each inversion we can store the difference and the index of the second element upon which we work. We sort this array and then for each inversion initialize the increment(x) as 0. till we reach x>diff we keep on adding ith value for ith operation and push the stored index in the array into our answer.
I used the following explanation to convince myself that the intended solution works:
In a permutation of 1 to n, 1 is the smallest number. It is the worst victim of inversion because it is the smallest. It needs our help the most. Now we have n chances to help this victim. What should we do? Of course we should give it the biggest help. How to give the number 1 the biggest help? It is obvious to place it (its position) at the end of our answer array. This is because in our answer array, we add i to the element and its suffix.
So, the number 1 needs the biggest help. The number 2 needs the second biggest help. The number n needs the least help.
The easiest approach on problem C
Yeah, I’m surprised this wasn’t the official solution. It guarantees that you are left with the array
[n + 1] * n + dwheredis some strictly non decreasing array.If you applied operation at index j, all differences will still the same except at the position j — 1 because: 1. all what after this position will increase with the same value 2. all what before this position will still the same
Note that if you have n items in a, you will have n — 1 differences
Can anyone explain me why my solution for D is wrong. I gave stored max score of path starting from each node. Then I gave ceil(k/no of child) to first (k%no of child) greatest node and floor(k%no of child) to other nodes. My codehere
With the input
your code gives 116 when the correct answer is 124.
The problem is that the maximum score of a path through vertex 2 is 102 (path 1-2-4), but once you have already sent a path that way, the next path is forced to go through vertex 3 instead of 4, so it has score 3. Instead, on the other branch, every path has cost 11.
Okay I get it now!
I think there is a typo in solution of step 4 for problem C. It should be $$${a_{i + 1} > 0}$$$
fixed, thanks
Hey, I think Problem B just need count the number 1 less than indices which is first non-zero element's indices in the sorted array.
there are many answers, but if I want to be honest I choose this because it was easy to proof! thanks
The code of D isn't clear enough to be understood, can anyone provide clean code?
It’s my code https://codeforces.net/contest/1746/submission/176359715
It would be better if he provided hints and steps.
Thank you for this contest and interesting problems.
However, please proof-read the statements in the verdict as well.
For E1, the wrong answer prints this statement: "you can't guess the answer in 2 chance!" And this led me to assume that I'm not allowed to guess the answer in 2nd chance.
When I thought about doing DP for D, it looked that for each vertex with n children and p paths to distribute, we had an exponential number of ways to choose n%p ones from the n children.
So one key observation is that larger number of paths always produce larger scores, so we can use greedy as shown in the editorial.
For Problem D, it turns out that if I always calculate
DP(child[v][i], k/cnt_child+1)no matter whetherk%cnt_childor not, then I might get TLE (I'm using C++ std::map to represent the second dimension of the dp array). So it looks that this optimization is necessary?Yes, consider a chain.
I came up with an example: if k = 5,6 and cnt = 3, then if we compute both k/cnt and k/cnt + 1 then the result will be 1, 2, 3 which will result in an exponential number of states.
Can somebody elaborate more on why this is happening? I mean at-most, we are calculating 2n states, why TLE then?
That's because the number of states may not be
2n.When
k%cnt == 0, $$${\lfloor k/cnt\rfloor, \lceil k/cnt\rceil, \lfloor (k+1)/cnt\rfloor, \lceil (k+1)/cnt\rceil}$$$ contains 2 numbers, butk/cnt, k/cnt+1, (k+1)/cnt, (k+1)/cnt+1could contain more than 2 numbers, which results in a chain of exponential numbers of states.I just recieved a message about coincidence with solutions and i admit that everything is my fault, i saw a solution on ideone.com and copied to sumbit.
A different "ideone" response for a change...
Hi MohammadParsaElahimanesh, I think you should explain why many solutions got FST on C, many of them would be unable to figure it out why it's wrong.
Thanks
One of my friend assumed that in the answer $$$a_{i-1}<a_i$$$ must be hold,but in fact it should be $$$a_{i-1} \le a_i$$$.
1
10
10 3 2 1 9 8 7 6 5 4
Oh, I also got hacked in a similar type of case a few contests back on the Array Recovery Problem:(
Hacked AC
Did your friend failed TC 46?
Hi, sorry but can you explain FST (I'm not familiar with) :) my guess: (Fail Sample Test)
some solutions be Hacked with
Fail System Test afaik
thanks,
above test may help you.
One of my worst rounds ever... but good job guys.
In solution for D, the fourth paragraph, should $$$\lceil (x/num)\rceil$$$ be $$$\lceil (x+1)/num\rceil$$$?
fixed, thanks
Can G be solved with simulate cost flow?
I solved problem D purely recursively (it's still DP, but simple enough to not need a separate array for each node), in a similar manner as described in the editorial, but with a twist.
Here's my code: 176372281
I have declared an array called "maxToHere", but I didn't need to use it after all. and forgot to remove it in contest.
Can you tell me what's wrong in my approach. For choosing which k%child children will get +1 extra path, I was finding X = (max score sum path starting from child and ending at any leaf node), then I gave +1 extra path to k%child children having largest value of X.
Look at this WA I had during contest: 176361876
Compare the differences between this code and the one that gives AC I linked above. That may help you understand what I mean with available path.
dp doesn't mean having some array. what you do is still dp, and it calculates same states.
I mean, I know almost any kind of memoization tends to be DP. For example, you could say that prefix sum is indeed DP, but it's as simple as just using a for loop.
What I meant to say is that you could skip checking multiple states for each node, with this sort of "greedy" approach, and avoid using a "dp" array altogether. The states are simple enough to make it recursive, but I understand your point.
In this case then, states are for each node are $$$(sum, maxpath)$$$, where:
It's a matter of something that you would surely call "DP on tree", becomes more like just "divide and conquer". The states explained like that may seem more clear to understand (or maybe not), but in this case I prefer to think of the process you go through to get to the solution approach. Nevertheless, I guess I will remove the parentheses in the previous comment to avoid confusion.
I get wrong answer on test 3 for problem F because I use rand() instead of mt19937. TAT
Is it?
For such an argument the constraints should include the number of test cases. As it was not public during the contest, I felt this was not reasonable. $$$(1 - 300000 \times 2^{-30})^m$$$ is about $$$0.97$$$ for $$$m = 100$$$ cases or $$$0.76$$$ for $$$m = 1000$$$ cases. I won't be happy to lose a whole score with this uncertainty.
In general — I always think that for problems with intended solutions being randomized, an upper bound on the number of test cases should be disclosed, or there should be no system tests (and no hacks). And since this can suggest the crucial idea of randomized solutions, it might be a good way to have a rule about global upper bound on the number of test cases. (... or does it exist somewhere I don't know?)
you are correct, but I think there is a limit on m naturally(but rules must contain it), I never saw problem with m more than 300 anyway and also consider all of (300000) queries are not on type 2(also in many queries probability is 1/k30 and k >= 3).
at end you could use 35 instead of 30, I myself use 50 in main solution(because it is model solution)
I'm sorry, you were unlucky
Check out this freaking problem with 753 test cases
1566G — Four Vertices
What makes it more funny is testdata is weak so some of the solution got uphacked.
128646349
Like 998244353 problems lol
For E, when you're down to three candidates, you can eliminate one with only 3 queries:
great, we use it in E2
Finally noticed this in Problem C after being dumbfounded yesterday:
"...all of its elements by
1i"I notice this after reading your comment
I fill terrible
wasted 30 mins on this! :) Got a sweet FST!
In the explanation of test sample 1, there is this line:
We must be adding i, not 1, for each operation in order to reach these numbers.
Is it just me, or editorials in codeforces are actually very bad?
It's not just you. It's at least two of us.
I think the reason is simple. There is some quality control for problems but there is none for editorials. Global rounds usually still have better editorials than ordinary ones though
Still usually much better than in atcoder
Strangely I feel the opposite tbh.
Can anyone say about the second question. I am not able to understand it
Yes if someone would explain it in simple sentences it would be much appreciated!
I have no idea what is described in the editorial. Here is my solution.
It's easy to see that for sorted array if you increase last element it's still sorted. Similarly, if you decrease first element it's still sorted. Taking into account that initial array consists of only zeroes and ones, this means you can reduce first 1 to 0 and increase last element repeatedly until array is sorted. It feels dumb. You can do better. Each 1 you take is good enough to fill gaps like 1 0 1 -> 1 1 1. But then notice that for gap 1 0 0 0 1 you want three ones. But what if test like this: 0 1 1 0 0 0 1? You can do following:
In other words, just two pointers approach. First pointer looking for one forwards, and second pointer looking for zero backwards. Then, move 1 -> 0 and it will make array better. I'm lazy to prove it.
Submission: 176323431
For Problem B-
I simply counted the number of 1s in the array, and all those elements should be at the right of the array, and the max element can be only 1 to AC your solution. Suppose n=10, and C(1)=5. Then all these one should be at the end of the array(i.e. index 6-10). So we directly have to count the number of 0s from the index n-c to n, and that's the answer.
Solution
In problem D, can anyone explain the difference between ⌈x/num⌉ and ⌈(x/num)⌉?
There is no difference... is that written somewhere in the editorial? I suppose it may have been edited afterwards.
In question E1 what if one is YES and other is NO . Any one of them can be a lie , In step 4 they have only mentioned the cases where both are either YES or NO.
Did you mean step 3? In any case, what's important here is that they cannot both be lies. If you have sets $$$A$$$, $$$B$$$, $$$C$$$, and $$$D$$$, you can query $$$A \cup B$$$ and then query $$$A \cup C$$$. There are four possibilities:
In all cases, we can eliminate one of the four sets.
I could easily understand (NO,NO), (YES,YES), but had difficulty in (NO,YES) and (YES,NO) cases.
For this, we can think along the following lines -
In AUB and AUC, if it says (NO,NO) we can definitely tell that one of them is correct and since A is common to both, the number definitely won't be in A.
Some stuff in logic (1) AUBUCUD = Universe (2) if S is YES, then (Universe — S) is NO.
using (1) and (2), we can have AUB is YES => (Universe — AUB) is NO => CUD is NO
Now, we can determine for all cases. For example, when there is (YES,NO)
AUB is YES => CUD is NO AUC is NO ------------------------- C is common. Thus, definitely not in C1746D - Paths on the Tree editorial is awful. You should at least mention that we solve it by dp over subtrees. Then, give an idea how to calculate value, and why it works. I would also mention why all balls should reach leafs. Also I would like to see proof of claim about floors and ceils.
My answer to how to calculate state of dp: you may think of it as all have $$$\lfloor x/num \rfloor$$$, and those who will have $$$\lceil x/num \rceil$$$ will be upgraded with bonus $$$f(u, \lceil x/num \rceil) - f(u, \lfloor x/num \rfloor)$$$. We want maximum bonus, so pick nodes with maximum bonus. Not hard to see why it works, even if bonus could be negative. But I don't know is it working to sort by $$$f(u, \lceil x/num \rceil)$$$.
I would like to see the proof on the floors/ceils as well. The suggested solution was the first thing that came to my mind, but I didn't know how many different choices I'd need to consider for each node. I was only able to observe that there are at most two values when $$$num = 2$$$ through considerable case analysis, and didn't know how the result would extend to larger divisors, and didn't feel comfortable with coding it when this number was unknown, as it would have significantly affected how the DP is set up (and I was worried there would be too many to pass the time limit).
intuitive way to prove there are at most two values
Why is D: 176443434 TLEing
If
dp[node][k]is 0, you cannot check if it was searched before correctly.In my solution, I had used dp.count({node,k}) to check if a state had been visited before and it still gave TLE. Are there any problems caused by count function too? 176444934
If
chis a divisor ofk, do not searchdfs(it, x + 1).Because it will make 2 states to 3 states, and it will have an exponential growth.
Problem D-->1746D - Paths on the Tree,I spent several hours trying to find the problem in my code, but it didn't work. Who can tell me what the error is in my code, and I still can't pass the second text case-->176451251
I want to share my alternative solution to 1746E1 - Joking (Easy Version)
I will use following notation: a — means query a returned NO, and A — means query a returned YES.
Notice aa — tells us a = NO. And AA tells us a = YES. But, you can't be sure you get aa or AA, so you may get aA or Aa and it doesn't tell anything. Next: aAA will tell a is YES, but you can get aAa and get nothing again.
So next my idea was aAbb -> at least give us b = NO. Or we can get aAbB, and you may guess a = b. But no! until the end of contest and several hours after I thought aAbB means a = b, but it's wrong. In terms of truth sequence aAbB may be false true true false, so a = YES and b = NO is possible, and it's not easy to tell.
Then, next my idea was to ask a twice again, in other words: aAbBaA. In this case indeed a = b. What else could be? it could be aAbBA, then a = YES for sure. otherwise we get: true, false, ?, ?, false. And two question marks should be opposite, so either we get two false from left or two false from right.
So, in 6 steps we can get either two same answers at once and tell about one question answer for sure. Or we can get relation a = b in case aAbBaA, or a != b in case aABbaA. Then, grab all relations of a = b and a != b and if they all connected in terms of graph, we can set value to one question a and then derive all other questions. This was main idea. But 6 steps is way to inefficient. But we can get answers for 17 questions about each bit and get result in 6*17 = 102 questions. Single question has all numbers where i-th is set.
Surprisingly, we can 'trim' useless questions: if we ask a, then b twice, we can get either:
So we can make graph from 17 questions about each bit, and fix single unknown and derive everything else. It require at most 17 * 4 queries.
Submission: 176399636
I think the first two here should be abBA and aBbA?
Anyway, this is a very interesting approach! I don't think we need to actually build a graph; we can, for example, set the first bit as a base and then ask questions in a chain like abbaccaddaeea... to determine other bits exactly or at least their relation to the base bit. When we determine the value of the base bit (Case 2), we update the previous bits that depended on it, set a new bit as the base bit, and start a new chain with it. Even if we cover 17 bits without determining whether the latest base bit is 0 or 1, we have two guesses to try both options.
I considered whether this can be adapted to solve E2, but I think the worst-case would be if we keep hitting Case 2 and reset the base, requiring $$$4 * 16 = 64$$$ questions. We don't need to determine the remaining one, since we have two guesses. However, this kind of "base reset" does not take advantage of the last element of the chain, e.g., if we get abBa, we might be able to utilize the last a somehow to keep the chain connected when we change the base. It might be possible somehow to avoid disconnecting the chain, allowing for 3 additional queries per bit (plus 1 to start the first one), resulting in 49 queries (suffices for E2).
We don't know about bits inside graph, only their relation. This is why we also need to check 17-th bit, because we either will know its value or relation. We do two guesses to try both possibilities for some node in graph. If you have proof of work in 49 queries I would like to look at it.
Problem B easier
Output the number of operations we did in step 2.
Code in Perl — 176389143
OMG, I haven't ever seen code in Perl, it looks like you wrote random symbols from your keyboard. Could you write a pseudocode in English?
Initially you have an array ARRAY and counter COUNT (initial value is zero).
WHILE ARRAY is not EMPTY DO
---- SHIFT ARRAY and CONTINUE IF the first element of an ARRAY is '0'
---- POP ARRAY and CONTINUE IF the last element of an ARRAY is '1'
---- increase COUNTER by 1
---- SHIFT ARRAY, POP ARRAY
END WHILE
PRINT COUNT
For D,how to strictly prove that the number of states is O(n)?
GOT IT!!!
Here is an interesting problem that I initially misread C to be — instead of increasing the all elements of the suffix by $$$i$$$, we increase them by $$$1$$$ in each operation. I've been thinking about this question and don't seem to be able to come up with a solution. Any ideas?
F can also be solved with a slightly different randomized solution. Let's create $$$k$$$ random maps $$$f_1, \ldots, f_k$$$ from the numbers in the array to, say, 32-bit integers. Then, we can check that a subarray satisfies the property for given $$$k$$$ by finding the sum of $$$f_i(a_l) + \cdots + f_i(a_r)$$$ for all $$$i$$$. All these sums have to be divisible by $$$k$$$, and the converse is true with very high probability.
ivan100sic can you please provide some explanation with examples? for eg if a[l..r] is: {1,1,1,2,2,2,3,3,3,3,3,3} for k=3 then for each random maps the sum will be divisible by k, but the answer is "NO". please let me know in case if I miss anything.
You're not summing $$$a_i$$$ but $$$f(a_i)$$$ which are random.
I am struggling with problem D for days and my solution didn't accepted till now, can any one figure out what is the problem with my code ? Any help will be appreciated.
understood finally, the optimal is sort according to the differences not the values.
I have a confusion. The editorial for problem D says that, for a certain tree structure, a particular node can have ONLY two possible values of cnt which is why we only need to work with a certain node for 2 times and save it in a memory because we might encounter the same state later. So according to the solution provided, for a certain node i, answer[i] is a vector which has size not more than 2. right? If so far what i understood is true, how can i logically prove that there are only two possible values of cnt for a certain node? Is there an intuitive way to prove this?
I add assert(answers[v].size() <= 2) in line 38 176651123 and it works !
about last question i must say that if all node with height h have at most two numbers, It's easy to prove this condition hold for all nodes with height h+1(see the proof in editorial)
Since x and num is integer and num >= 1, let's observe this sequence of numbers:
for any adjacent elements in this sequence, it is impossible that (x/num) < A and A < (x+1)/num and A is integer ( if you want x/num and (x+1)/num cross some integer A, at least one of them will be integer. ) so $$$\lceil (x+1)/num \rceil - \lfloor x/num \rfloor \le 1$$$.
below is an illustration when num is 3: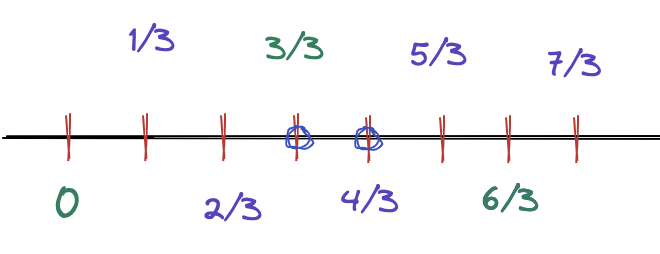
(I hope this helps, forgive my poor English :)
Thank you so much for your explanation. And your English is good. :D
For people who solved E1: how do you reach the $$$abba$$$ construction in E1, or how did you reach your construction for $$$n = 3$$$?
n=3 for me was built on the explanation of the example (using one of the two guesses to either solve it or force a non-joking answer)
For the main construction I calculated what the possible answers to a pair of queries could mean. For yes yes to reduce the search space you need something not in either query, for no no you need something in both queries and if the responses are different (yes/no, no/yes) you need something unique in the no query which suggests that splitting into 4 would be best.
For C, why don't 1 2 3 4 ... n works?? for example if we take a case 3 2 4 1 my answer for this is 1 2 3 4 dry run : i = 1 -> 4 3 5 2 i = 2 -> 4 5 7 4 i = 3 -> 4 5 10 7 i = 4 -> 4 5 10 11
but this logic is giving me wrong answer, what am i missing??
Hi, consider 4 1 2 3 it will be 5 4 8 13 and it is not sorted
MohammadParsaElahimanesh, can you please help in question 1746D - Paths on the Tree. Like understood what is written in the editorial properly but the most confusing thing is how you write dfs I.e. recursive function so clean without any error. Like what I want to ask you is , in my case to understand your dfs implementation part I am going deep into recursion like this function is calling these inner functions and so on and actually it bec0mes very confusing.
So do you just write dfs assuming that the function calling will give me the correct result like in case of DP. And all I have to do is working on the current state without any worry of how all other states will work and they will work correctly. So how do you think sir during writing dfs ??
sorry for poor english in advance, we can calculate answer for some subtree and it does not relate other nodes, because each time we go down in tree and do not repeat some node in one way
Sir, I did not get it what are you trying to say? Can you please help me explain more elaborately/ clearly??
about your above question,you are right, it is same as simple dp, also i tell my friend(AmirrzwM) to help you if he can.
MohammadParsaElahimanesh, sir only last time I will disturb you can you please tell in submission 176328072, what the 2nd last line I.e. dl += ws[rs] is doing??. Very Sorry if I am irritating you by pinging you again and again but I genuinely do not get the point what 2nd last line in dfs function is trying to do ??
dl += ws[rs] means if we call node k one times more, how much score can we reach, so dl = w[k]+ws[rs]
note we will pick ws 0 1 2 3 4 5 ... rs-1 surely and ws rs if we call some node one times more
But, Why we need to call node k one time more?
My thought: I think it is because our main objective is not only to calculate the answer in dfs function but we also have to return to the main function its calculated dfs function answer.
Am I thinking correct sir ??
no, It's not true, please read toturial agin, i calculate dp1 and dp2 but he calculate them together
I think now I am irritating you, but I have read the editorial many times and your code is looking correct to me but in this submission 176328072 I am genuinely not getting why we need to add node k one time more I.e dl= w[k] + ws[rs] ??
Can you please last time explain MohammadParsaElahimanesh??
You can look at this submission also if you want , both are written in same way but here also last line did not make sense to me 176439185
no problem, but at least like my massages :)
consider node v, it has m children and we want to calculate "what is the answer if k balls reach to v" we name it dp v, k. the most important point is if k balls reach node v. k/m+1 balls will reach to k%m children of v and k/m balls will reach m-k%m children of v. or in another word, one more ball reaches to k%m children of v.
so we can use dfs and it returns a pair {dp[ch][k/m], dp[ch][k/m+1]} where ch is children of v
sorry for poor english
My algorithm to 1746C keeps failing
My Algorithm:
Step 1: Reverse loop the array and increment the element if the difference from the consecutive previous element is negative. Step 2: How to find the increment? Finding an increment is straight forward. Basically, this is an Arithmetic Progression: So, Sum of N elements is:
Hence, there is a quadratic equation that I need to solve.
Step 3: Keep doing it till the array contains elements in non-decreasing sorted order. Step 4: If the array is already sorted, but we still have operations left, then just increase all array elements by that current operation increment. My Submission link which is failing: https://codeforces.net/contest/1746/submission/177280199
Take a look at Ticket 16322 from CF Stress for a counter example.
I authored a similar approach: https://codeforces.net/contest/1746/submission/177047158
Can you please guide me where is this failing?
The editorial for problem D is too simple. It's hard to understand. I'm Chinese. When I participant in some Chinese algorithm contests, say, Nowcoder contests, the editorials are mostly hard to understand even though they're written in Chinese. I don't know why. Maybe I'm a newbie, and the editorial is for those experts to read.
I read the code. I sort of understand. Maybe this is what called "talk is cheap, show me the code". Anyway, thank you.
Fun fact: the author's solution of problem D is $$$O(n \log n)$$$ because it sorts the children by the best "extra" path, but it can actually be improved to $$$O(n)$$$ with
std::nth_element(which uses the Introselect algorithm). The idea is that we only need to partition the elements according to the $$$j$$$-th largest element for some $$$j$$$, and we don't care about their relative order beyond that.177698814
I know it's very, very far out of my league but I saw flows in the tags for G, I tried to think of a way to setup a min cost max flow network that would solve the problem at all, even if it is not the intended time complexity.
I thought of two ways but they both have issues and I don't know how to (or even if it's possible to) combine them.
First was that to ensure that the numbers of tasks are what I need, I would create three nodes for each type of task and they have capacities $$$a$$$ $$$b$$$ and $$$c$$$ going into the sink
The second was to handle deadlines I create a node for each day, connect it to sink with capacity 1, connect a task to it's deadline and connect each day to the previous one, signifying that you can do a task with a deadline $$$d$$$ on $$$d-1$$$ but not the other way round.
Any help would be really appreciated.
link
Next time search through original blogpost as well
Thank you!
I don't get the idea of this statement in problem F:
It's not so hard to prove that the probability is equal to 1/2 for k=2. As I understand, instead of checking the number of occurrences of every single number, the intended solution will sum up all the number of occurrences of each number in the set $$$S$$$. However, if $$$|S| = 4$$$ the probability of concludingYESwhen the actual answer isNOshould be $$$\dfrac{7}{8}$$$, and this probability is even higher with a larger $$$|S|$$$. What is wrong with my thinking?E = Even, O = Odd, $$$k = 2$$$
E E E E -> only this case
YESE E O O
E O E O
E O O E
O E E O
O E O E
O O E E
O O O O
The array isn't random; the subset is random.
I get it, thank you!
In problem C, step1 -> solution there is a typo
stpesthank you.
For those who are interested.
Problem E1/E2 is similar to https://www.codechef.com/JUNE20A/problems/GUESSG (Editorial).
.
Can anyone explain me what's the space complexity of this code,I am getting MLE on test case 2. here's my submission: https://codeforces.net/contest/1746/submission/202337720
Hint :
resizedoesn't do what you think it does. In fact, if you don't use the correct version of resize, then regardless of space complexity, your algorithm would also give WA. Can you see why?but now my code is giving TLE on test case 25. https://codeforces.net/contest/1746/submission/202518774 I don't think collisions occur in maps and when I saw other people's code,so they have used different method to store the answer than mine. can u give me some idea to optimise this approach or rough time complexity of this code
the technique used to solve problem F , is that a renowed trick , are there more problems on that trick.
for D, why do we need a base case in DP ? How could it happen that we enter a node twice?
In problem E2, number of needed questions seems to be 3*(log2(n)+1).
Can someone please explain why the time complexity of problem D is O(n). why number of states in O(n) ? Why cnt can only be two adjacent integer (x,x+1) ?
Thanks in advance
Why is my submission 303635606 on 1746C - Permutation Operations getting wrong answer?