404A - Валера и X

В данной задаче нужно было проверить, выполняются ли ограничения, описанные в условии. Чтобы это сделать, можно было завести два множества. В одно множество сложить диагональные элементы матрицы, в другое — остальные. Элемент a_i, j стоит на главной диагонали, если i = j, и стоит на побочной, если i = n - j + 1. После того, как мы сложили все элементы в множества, нужно проверить, что размеры обоих множеств равны единице, и элементы этих множеств различны.

404B - Марафон

В этой задаче нужно было заметить, что пройдя расстояние 4·a, Валера окажется в той же точке, откуда стартовал. В момент, когда Валера получит i-ое питание, он пробежит расстояние i·d. Давайте посчитаем величину 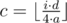— сколько полных кругов пробежит Валера по стадиону. Тогда на своем последнем кругу Валера уже пробежал L = i·d - c·4·a метров. В зависимости от этого L можно легко определить позицию Валеры. Например, если 2·a ≤ L ≤ 3·a, то Валера будет находиться в точке с координатами (3·a - L, a). Аналогичным образом разбираются остальные 3 случая.

404C - Восстановите граф

Заметим, прежде всего, что в массиве d должен быть один и только один 0. При этом d[start] = 0 обозначает, что start именно та вершина, от которой Валера считал расстояние до всех остальных. Заметим, что любая вершина u, для которой d[u] = i должна быть соединена ребрами только с вершинами v, у которых d[v] ≥ i - 1. При этом хотя бы для одной вершины v₀ из соседей u должно выполняться d[v₀] = i - 1. Будем строить искомый граф добавляя по одной вершине в порядке увеличения их расстояния до start. Изначально в нашем графе будет одна вершина с номером start. При добавлении вершины u с d[u] = i рассмотрим все вершины v, у которых d[v] = i - 1. Выберем среди таких вершин вершину минимальной степени. Если эта степень равна k, то ответа не существует. Иначе добавим в граф вершину u и ребро (u, v). Если вершин с расстоянием до start равным i - 1 нет, то ответ также  - 1. В противном случае после добавления всех вершин, мы получим граф, удовлетворяющий условиям задачи, который при этом будет деревом, а значит количество ребер в нем n - 1 ≤ 10⁶.

404D - Сапер 1D

Задача решается методом динамического программирования. Будем считать d[i][type] — количество корректных способов заполнить префикс полоски длиной i так, что последняя заполненная клетка имеет один из пяти типов. Типы последних клеток будут следующие:

1. в клетке записано "0"

2. в клетке записано "1" и слева от нее стоит бомба

3. в клетке записано "1" и слева от нее нет бомбы

4. в клетке записано "2"

5. в клетке находится бомба

Когда мы хотим заполнить очередную клетку, мы перебираем, что туда запишем, и проверяем два условия. Во-первых в заданной строке значение заполняемой клетки должно либо совпадать с тем, что мы хотим записать, либо быть равно "?". Во-вторых новый префикс должен оставаться корректно заполненным. Это значит, например, что если мы находимся в состоянии (i, 1) (то есть в последней заполненной клетке записан "0"), то в следующую клетку мы можем либо записать "0" и перейти в состояние (i + 1, 1), либо записать "1" и перейти в состояние (i + 1, 3). Записать "2" мы не можем, так как у клетки с "2" оба соседа должны быть заполнены бомбами. Поставить бомбу после "0" мы не можем по очевидным причинам. Обратите внимание, что записав "1" после "0" мы переходим именно в состояние (i + 1, 3), а в состояние (i + 1, 2) мы можем перейти лишь записав "1" после бомбы. Аналогичным образом разбираются остальные переходы динамики.

404E - Лабиринт 1D

Рассмотрим случай, когда последовательность ходов робота заканчивается буквой "R". Если она заканчивается на "L", то можно заменить в исходной строке все "L" на "R" и все "R" на "L" и ответ от этого не изменится. Покажем, что количество препятствий, которое потребуется Валере, не превосходит 1. Предположим Валера поставил препятствия в какие-то клетки. Будем говорить, что номер препятствия — это номер клетки в которой оно стоит. Рассмотрим среди всех препятствий с отрицательными номерами самое правое (обозначим его obs1), а среди препятствий с положительными — самое левое (обозначим его obs2). Очевидно, что робот не сможет оказаться левее препятствия obs1 и правее obs2. Поэтому требуемое количество препятствий не превосходит двух. Покажем, что Валере не нужно ставить препятствия в клетки с номерами больше нуля. Предположим он поставит препятствие в клетку с номером a > 0. Если робот ни разу не попытается сходить в эту клетку, то, очевидно, препятствие лишнее. Если в какой-то момент робот пытается пойти в клетку a, то в последующем он посетит финишную клетку более одного раза. Это так, потому что на последнем ходу роботу нужно пойти направо, но из клетки a - 1 направо пойти нельзя, а все клетки, которые левее уже были посещены. Таким образом мы получаем, что Валере потребуется не более одного препятствия, которое должно иметь номер меньше нуля.

Давайте теперь проверим, может ли Валера обойтись вообще без препятствий. Если может, то робот не пропустит ни одного хода и успешно закончит выполнение инструкции в какой-то клетке. Тогда Валера может выбрать только эту клетку в качестве финишной и ответ на задачу в этом случае равен единице. Остается случай, когда Валера должен поставить одно препятствие.

Заметим, во-первых, что по тому, где Валера поставил препятствие, однозначно восстанавливается финишная клетка. Это значит, что количество способов выбрать препятствия и финишную клетку, равно количеству клеток, в которые нужно поставить одно препятствие. Предположим Валера поставил препятствие в клетку с номером b < 0 и робот успешно закончил инструкцию. Заметим, что в этом случае робот пропустит какие-то ходы типа "L", выполнит все ходы типа "R" и последним своим ходом пойдет направо в какую-то не посещенную клетку. Если теперь мы подвинем наше препятствие на одну клетку вправо, то от этого робот может лишь пропустить больше ходов типа "L". Это значит, что финишная клетка может лишь подвинуться вправо. Но так как в прошлый раз мы ее посетили последней, то и новую финишную клетку мы посетим последней. Это в свою очередь значит, что существует какая-то клетка p < 0 такая, что если мы поместим препятствие во все клетки c ≥ p, то робот сможет успешно выполнить инструкцию, а если поместим препятствие в клетку d < p, то не сможет. Эту клетку p можно найти при помощи бинарного поиска и простого моделирования за O(n) на каждой его итерации. Таким образом получаем решение за O(n log n).