We've talked about Generating Functions in the past blogs, but this time we are going to explain about it in a better way, as I think last time's note was really messy.
First let's have a look at this problem: how many subsets $$$s$$$ of $$$S=\lbrace 1,2,3,4,5\rbrace$$$ are there which fit:
- The sum of all the elements in $$$s$$$ is $$$k$$$.
This may be a very traditional problem, let's see the solution below:
- Let's construct a function $$$f(x) = (1 + x) (1 + x^2) (1 + x^3) (1 + x^4) (1 + x^5)$$$, and let's expand it into $$$1 + x + x^2 + 2 x^3 + 2 x^4 + 3 x^5 + 3 x^6 + 3 x^7 + 3 x^8 + 3 x^9 + 3 x^{10} + 2 x^{11} + 2 x^{12} + x^{13} + x^{14} + x^{15}$$$. And if you are getting the result of $$$k$$$, just look up the coefficient of $$$x^k$$$. If you don't believe this, let's just write it out:
Denote $$$\text{sum}[array]$$$ to the sum of the array.
- $$$\text{sum}[]=0$$$.
- $$$\text{sum}[1]=1$$$.
- $$$\text{sum}[2]=2$$$.
- $$$\text{sum}[1,2]=\text{sum}[3]=3$$$.
- $$$\text{sum}[1,3]=\text{sum}[4]=4$$$.
- $$$\text{sum}[1,4]=\text{sum}[2,3]=\text{sum}[5]=5$$$.
- $$$\text{sum}[1,5]=\text{sum}[2,4]=\text{sum}[1,2,3]=6$$$.
- $$$\text{sum}[1,2,4]=\text{sum}[2,5]=\text{sum}[3,4]=7$$$.
- $$$\text{sum}[3,5]=\text{sum}[1,2,5]=\text{sum}[1,3,4]=8$$$.
- $$$\text{sum}[2,3,4]=\text{sum}[1,3,5]=\text{sum}[4,5]=9$$$.
- $$$\text{sum}[1,2,3,4]=\text{sum}[2,3,5]=\text{sum}[1,4,5]=10$$$.
- $$$\text{sum}[1,2,3,5]=\text{sum}[2,4,5]=11$$$.
- $$$\text{sum}[1,2,4,5]=\text{sum}[3,4,5]=12$$$.
- $$$\text{sum}[1,3,4,5]=13$$$.
- $$$\text{sum}[2,3,4,5]=14$$$.
- $$$\text{sum}[1,2,3,4,5]=15$$$.
And you are finding that, the two ways we've been using, are getting the exactly same results. Why is it working? Well, you can understand it emotionally, just like the way we prove special binomial theorem.
But wait, don't you think that, the function looks seemingly out of the blue. So let's explain it.
First, we find that if we are counting the numbers of different subsets, the equation should be $$$(1+1)(1+1)(1+1)(1+1)(1+1)=32$$$. It's really similar to the function we constructed, but turned $$$1$$$ to $$$x^i$$$.
Just as what we said the last time, the $$$x^i$$$ can be considered as a simple simple, without caring what $$$x$$$ actually represents.
We can concretize the function:

We can find that, merging the options by $$$\text{and}$$$ operation is the same as multiplying them together, according to the multiplication theorem. Also, according to the addition theorem, we can consider the $$$\text{or}$$$ operation as the result of adding the elements together.
But in this task it's different. Choosing both leads to sum instead of product. So let's consider a way to turn multiplication into addition. Clever readers may find out that, exponent arithmetic is a good way. Since $$$x^a\times x^b=x^{a+b}$$$.
To choose $$$x$$$ in your subset, the index should be $$$x$$$, otherwise it should be $$$0$$$. Since $$$x^0=1(x\not=0)$$$, we can turn the concretized funtion into the maths function:
Or:
Here we go. You may be confused that the whole thing we have been doing has something conflicting: there are two different addition operations here, one is index addition, one is addition between elements. The first operation is addtion in the problemset, the second one is $$$\text{or}$$$ operation. If you are not only interested in one item in the function, you can let $$$x$$$ be more complicated values, say $$$x_0$$$, and calculate the value of $$$f(x_0)$$$, which may be what you are interested in.
Here is a simple example. If you are going to count the number of subsets $$$s$$$ of $$$S=\lbrace 1, 2, 3, \dots, 2000\rbrace$$$, which fit:
- The sum of all the elements in $$$s$$$ is $$$5t$$$, $$$t\in\mathbb {N}$$$.
Then it means we only need to care the coefficients before 5-divisible-indexed items. Just make $$$x=\zeta$$$, which fits:
According to the basic theorem of algebra, the function has $$$5$$$ different roots
on a complex plane, which fits $$$\zeta_1=1$$$. Let's visualize the roots:
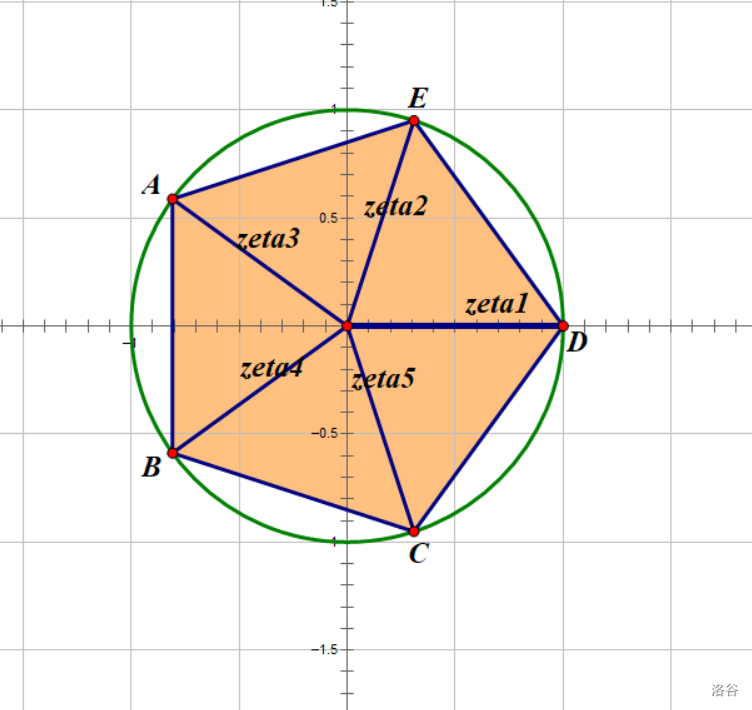
Actually, $$$\zeta_2^2=\zeta_3$$$, $$$\zeta_2^3=\zeta_4$$$, $$$\zeta_2^4=\zeta_5$$$, $$$\zeta_2^5=\zeta_1=1$$$. So, any one of $$$\zeta_2,\zeta_3,\zeta_4,\zeta_5$$$ can be $$$x$$$ in $$$f(x)$$$. Here we make $$$\zeta=\zeta_2$$$.
Then the function $$$f(x)$$$ is:
$$$f(x)=((1+\zeta)(1+\zeta^2)(1+\zeta^3)(1+\zeta^4)(1+\zeta^5))^{400}$$$
Then calculate the value of this function is okay, if you expand it, you will find only 5-divisible indexes are kept. To calculate the value of this function is no our point today, if you are interested in this, you can watch 3Blue1Brown's video about this. I'll link it later.
This is the first usage of this function.
Now let's consider another usage of this function: we talked about recurrence relations before. Now we're going to solve them by generating functions.
For example, considering the fibonacci array:
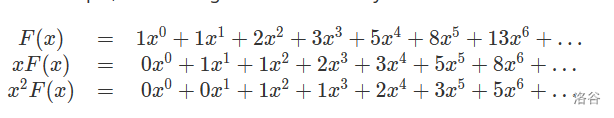
So, $$$F(x)+xF(x)+x^2F(x)=0$$$, then $$$F(x)=\dfrac{1}{1-x^2-x}=\frac{1}{\sqrt{5}}\left(\frac{\phi}{1-\phi x}+\frac{1 / \phi}{1+x / \phi}\right)$$$.
There are far more ways to use the generating function, this is only an example. If you are still interested in this, you can leave a friendly comment and I'll check it and write more about it.
Also, if I'm not writing this blog, my knowledge on this will be limited. I hope that this blog will not only help you but also you guys. Thanks for reading.










is there any way to solve the first example problem with time complexity better than O(n^2) (O(n * sqrt(n)) or better))