Совсем недавно завершилась очередная личная интернет-олимпиада на сайте http://neerc.ifmo.ru/school/io/index.html. Предлагаю обсудить здесь задачи. Особой интерес представляют задачи C и D. :) Как их решить на полный балл?
Вот задачи: http://neerc.ifmo.ru/school/io/archive/20140322/problems-20140322-individual.pdf. И результаты, если кто-то ещё не видел: http://neerc.ifmo.ru/school/io/archive/20140322/standings-20140322-individual.html. ;)
Последняя просто решалась sqrt-эвристикой по запросам. Сделаем корень добавлений, потом пройдемся по массиву, глянем какие элементы стали "хорошими". Для каждого такого элемента еще раз пройдемся по запросам этого блока, чтоб уточнить когда именно он стал хотя бы b[i].
Точно. Спасибо. =)
Я решал чуть (ну как чуть...) извращённей — персистентным деревом отрезков. Построим дерево, в вершинах будем хранить x, y и левый конец запроса. Тогда значение в определённой клетке после нескольких запросов сможем посчитать за log n, просто пройдясь вниз от вершины до листа и собрав все значения. Для каждого элемента массива найдём бинпоиском первую такую версию, где он не меньше b[i]. Итого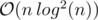
времени и 
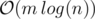памяти, чего еле-еле хватило.
Аналогично :)
а как делать добавление блока запросов за O(N) ?
Там же У меняется ( у*(i — L) ) для L<=i<=R
Это можно сделать, например, вот таким образом:
создадим два массива xx и yy; xx[i] — сколько нужно добавить к текущему числу в позиции i и yy[i] на сколько нужно увеличить коэффициент возрастания числа в позиции i.
тогда каждый запрос можно сохранить с помощью таких четырёх операций(l[j], r[j], x[j], y[j] — текущий запрос, l — левая граница, r — правая граница, x — начальное числа, y — возрастание):
Более детально: http://pastebin.com/u5jAseLC.
Круто! Спасибо :)
Добавил в тренировки 2013-2014 Цикл интернет-олимпиад. Седьмая личная олимпиада (22 марта 2014 года)
а может стоит выкладывать блоги про олимпиады, до их начала? а то я вечно пролетаю..
К сожалению, в данный момент у нас нет человека, который готов регулярно писать подробные анонсы про эти олимпиады, а писать что-то совсем короткое для галочки тоже не хочется.
Уже есть договоренность, что в следующем году этим будет заниматься кто-то из пресс-службы NEERC и всех остальных соревнований, проводимых в ИТМО.
Третья решалась так:
Сделаем бин. поиск по ответу. Чтобы проверить, подходит ли нам такой ответ, для начала увеличим радиус всех окружностей на R (R — текущий радиус, который мы проверяем). После этого останется проверить, что существует луч из стартовой точки, который имеет с каждой окружностью хотя бы одну общую точку. Для проверки этого проведем из стартовой точки касательные ко всем окружностям, получим набор углов (те окружности, в которых наша точка уже лежит, не будем рассматривать). Теперь осталось проверить, пересекаются ли все эти n углов (на самом деле, эти углы можно рассматривать как отрезки на окружности). А это делается уже довольно просто. Например, сортировкой и сканирующей прямой. Можно проверять и за линию, но заходила и сортировка.
К сожалению, во время контеста выяснилось, что решение жюри содержит ошибку (как раз в проверке того, что все углы пересекаются), приношу свои извинения за эту недоработку :(
А как проверять пересечение за линию?
Лично я писал решение с сортировкой, но за линию вроде можно делать как-то так:
Две касательные — два угла, то есть отрезок на окружности. Надо проверить, имеют ли несколько отрезков на окружности общую точку. Ну а это как-то довольно просто делается. Так как они лежат на окружности, а не на прямой, будут вылезать случаи, но если аккуратно написать, все должно быть хорошо.
Вот про "это как-то довольно просто делается" собственно и вопрос :-)
Ну, окей. Во-первых, мы явно может понять, какая касательная будет левым концом, а какая правым (просто по построению). Осталось пересечь отрезки. Для этого нужно только уметь пересекать два отрезка. А это делается просто разбором случаев (оба отрезка не проходят через 0, один проходит через 0, оба через ноль)
Может быть, можно и проще, это то, что первое в голову пришло :)
Ой, да, что-то я ступил. Спасибо.
Добавил все недостающие личные интернет-олимпиады 2014, вот полный список:
О, здорово, спасибо :)