PC Educational Round was conducted by Programming Club, IIT Madras. The problems were based on Logic, Data Structures and Algorithms with particular emphasis on Graphs and Dynamic Programming.
Here is the editorial with explanation and solution for each problem.
Link to contest : PC Educational Round
If you are unable to view the problems, then click on above link first.
A. Candice's Chocolates
Problem Author: RSG_02
According to the problem statement, each friend should get at least one chocolate. So, if $$$n<m$$$, the division is not possible and the answer is $$$-1$$$.
If $$$n \geq m$$$, then, as per the problem statement, $$$n$$$ chocolates have to be divided into $$$m$$$ friends such that every friend gets the same number of chocolates, while getting the maximum possible number of chocolates. This means, each friend gets $$$\left \lfloor{\frac{n}{m}} \right \rfloor$$$ number of chocolates.
Thus, Candice gets $$$n \% m$$$ chocolates, which is the answer.
#include <bits/stdc++.h>
using namespace std;
int main()
{
int t;
cin >> t;
while(t--)
{
int n, m;
cin >> n >> m;
if(n < m)
cout << -1 << "\n";
else
cout << (n % m) << "\n";
}
}
B. Kiteretsu's Game
Problem Author: AdC_AB2
Let's consider the string $$$s$$$ to have elements $$$s_1, s_2, \ldots, s_n$$$.
Consider $$$n \ge 2$$$. Then, all characters in the string can become equal only if there exists an index $$$j < n$$$ such that $$$s_j = s_{j+1}$$$.
If there exists no such $$$j$$$, then no operation can be done on the string, and all characters cannot become the same.
Consider $$$n > 2$$$. It can be shown that the string can ALWAYS be made to have $$$1$$$ distinct character if there exists an index $$$j < n$$$ such that $$$s_j = s_{j+1}$$$.
If we have such a pair, we can apply the first operation repeatedly with index = $$$j, j-1, j-2, \ldots, 1$$$. We can then apply the second operation repeatedly with index = $$$j+1, j+2, \ldots, n-1$$$.
From Hint $$$1$$$ and Hint $$$2$$$, we can say that for strings with $$$n \ge 2$$$, the string can be made to have only $$$1$$$ distinct character if and only if there exists an index $$$j < n$$$ such that $$$s_j = s_{j+1}$$$.
Strings of length $$$1$$$ already satisfy the $$$1$$$ distinct character condition.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solv()
{
ll n; cin>>n;
string s; cin>>s;
if(n==1)
{
cout << "YES\n";
return;
}
for(ll i=0; i+1<n; i++)
{
if(s[i]==s[i+1])
{
cout << "YES\n";
return;
}
}
cout << "NO\n";
return;
}
int main()
{
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int t; cin>>t;
while(t--)
{
solv();
}
return 0;
}
C. Lazy Oggy
Problem Author: Jigly_Puff
Sliding Window
We use the Sliding Window Technique here.
The use of sliding window algorithm can be done in specific scenario where the size of window is fixed. Find the size of window required in this case which is $$$k$$$. Compute the result for first window. Then use a loop to slide the window by $$$1$$$.
#include <bits/stdc++.h>
using namespace std;
void solve()
{
int n, k;
cin >> n >> k;
int a[n];
for(int i = 0; i<n; i++)
cin >> a[i];
int sum = 0;
for(int i = 0; i<k; i++)
sum += a[i];
int m = sum;
for(int i = k; i<n; i++)
{
sum -= a[i-k];
sum += a[i];
m = max(m, sum);
}
cout << m << "\n";
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
cin>>t;
int t1 = t;
while(t--)
{
// cout<<"Case #"<<t1-t<<": ";
solve();
}
}
D. Isn't it Odd?
Problem Author: s.tharun_dyanish
Use dynamic programming.
Let $$$c_i$$$ represent the number of ways to reach the block of index $$$i$$$. Now think of ways to reach this block from previous blocks.
Let us model this solution using dynamic programming.
Let $$$c_i$$$ is the number of ways to reach the block of index $$$i$$$. The value $$$c_n$$$ would be our answer.
To reach the block of index $$$i$$$, Dora can always jump from the previous block (of index $$$i-1$$$) and see also from block of index $$$i-2$$$ if weight of that block ($$$a_{i-2}$$$) is even.
So the number of ways to reach block $$$i$$$ ($$$c_i$$$) is $$$c_{i-1}$$$ ( $$$+c_{i-2}$$$ if $$$a_{i-2}$$$ is even). Iterating the array once with the above step being done for every $$$i$$$ will yield the answer for $$$c_n$$$.
#include<bits/stdc++.h>
using namespace std;
const int M = 1e9+7;
void solve()
{
int n;
cin >> n;
int a[n];
for(int i = 0; i<n; i++)
cin >> a[i];
int dp[n];
memset(dp,0,sizeof(dp));
dp[0] = 1;
for(int i = 1; i<n; i++)
{
if(i >= 2)
{
if(a[i-2] % 2 == 0)
dp[i] = dp[i-2];
}
dp[i] += dp[i-1];
dp[i] %= M;
}
cout << dp[n-1] << "\n";
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
cin>>t;
int t1 = t;
while(t--)
{
solve();
}
}
E. Samosa!
Problem Author: s.tharun_dyanish
Having a look at the constraints of $$$n$$$, realise running the whole process in $$$O(n)$$$ time won't pass, it will exceed the time limit.
Compute the expression of the final result, and try to calculate it in less than $$$O(n)$$$ time, in either $$$O(1)$$$ or $$$O(logn)$$$ depending on the expression.
Simulating through the process by hand, we realise Motu has
$$$n_1+n_2$$$ samosas after 1 round.
$$$2\cdot max(n_1,n_2)$$$ samosas after 2 rounds ($$$(n_1+n_2)+|n_1-n_2|$$$).
$$$ \quad \vdots$$$
- If $$$r$$$ is even Motu has $$$2^{\frac{r}{2}} \cdot max(n_1,n_2)$$$ samosas, if $$$r$$$ is odd, Motu has $$$2^{\lfloor \frac{r}{2} \rfloor} \cdot (n_1+n_2)$$$ samosas after $$$r$$$ rounds.
Now we can find the corresponding power of $$$2$$$ using binary exponentiation in $$$O(logn)$$$ time complexity. $$$Ans$$$ mod $$$10^9+7$$$ has to be reported.
#include <bits/stdc++.h>
using namespace std;
const int M = 1e9 + 7;
int64_t power(int64_t n, int64_t k, int64_t m)
{
n = n%m;
if(k == 0)
return 1;
int64_t res = power(n,k/2,m) % m;
if(k % 2 == 0)
return (1LL * res * res) % m;
else if(k % 2 != 0)
return (1LL * (res * res) % m * n) % m;
}
void solve()
{
int r,a,b;
cin >> r >> a >> b;
int64_t ways;
if(r & 1)
ways = power(2, r/2, M) * (a + b);
else
ways = power(2, r/2, M) * max(a,b);
cout << (ways % M) << "\n";
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
cin>>t;
int t1 = t;
while(t--)
{
solve();
}
}
F. Bob the Builder, Can we connect them?
Problem Author: AdC_AB2
Let's look at the different possibilities for $$$t_{max}$$$ = The maximum time taken to travel between a pair of islands in the constructed bridge combination.
- $$$t_{max} = 10^{10}$$$ if and only if the graph formed by the islands as vertices and bridges as edges is not a connected graph. The minimum number of edges required to connect $$$n$$$ vertices is $$$n-1$$$ (by forming a tree).
Hence, $$$t_{max} = 10^{10}$$$ iff $$$m \le n-1$$$.
- If the graph is connected, then we can ensure that the maximum distance between any $$$2$$$ nodes is $$$2$$$. This can be done by choosing $$$1$$$ node as a "hub" node, and connecting all other nodes to it. This construction is a tree and requires $$$n-1$$$ edges.
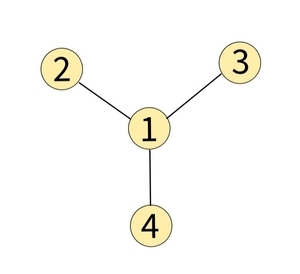
The image illustrates the hub connection mentioned above.
- For $$$t_{max}$$$ to be $$$1$$$, we need an edge between every pair of islands i.e. $$$m = \frac{n(n-1)}{2}$$$.
Let's call the number of pairs of islands with travel time = $$$t_max$$$ as $$$p$$$.
- For the case of $$$m < n-1$$$, we can show that $$$p$$$ is minimized if and only if we form a single tree of $$$m+1$$$ vertices and the remaining vertices are left isolated. In this case, $$$p = \frac{n(n-1)}{2} - \frac{m^2 + m}{2}$$$
Instead of assuming having 1 tree, let's say we have $$$c$$$ trees, with the $$$i^{th}$$$ tree having $$$d_i$$$ vertices in it. Then, the number of pairs of edges with distance between them $$$\ne t_{max}$$$ is $$$\sum_{i=1}^{c} {d_i \choose 2} $$$, which is to be maximized. Let's call this sum $$$S$$$.
$$$S = \sum_{i=1}^{c} {d_i \choose 2} $$$ = $$$\sum_{i=1}^{c} \frac{d_i (d_i - 1)}{2}$$$ = $$$\sum_{i=1}^{c} \frac{(d_i - 1 + 1)(d_i - 1)}{2}$$$
Let $$$d_i - 1$$$ = $$$e_i$$$ = number of edges in the $$$i^{th}$$$ tree.
Hence, $$$2S = \sum_{i=1}^{c} (e_i + 1)e_i = \sum_{i=1}^{c} e_{i}^2 + m$$$.
From RMS inequality, $$$\sum_{i=1}^{c} e_{i}^2 \le (\sum_{i=1}^{c} e_{i})^2 = m^2$$$.
Hence, S = $$$\frac{m^2 + m}{2}$$$ and the answer is $$$\frac{n(n-1)}{2} - \frac{m^2 + m}{2}$$$.
For the case of $$$m \ge n-1$$$ and $$$m \ne \frac{n(n-1)}{2}$$$, $$$p = \frac{n(n-1)}{2} - m$$$. In this case, we have to count the number of pairs of islands that have distance between them to be more than 1, which is equal to the number of pairs of islands that don't have a bridge between them.
For $$$m = \frac{n(n-1)}{2}$$$, $$$p = m$$$.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solv()
{
ll n,m;
cin>>n>>m;
ll val = 1e10, tot = n*(n-1)/2;
if(m < n-1)
{
cout << val << ' ' << tot - m*(m+1)/2 << endl;
}
else if(m < tot)
{
cout << 2 << ' ' << tot - m << endl;
}
else
{
cout << 1 << ' ' << tot << endl;
}
}
int main()
{
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int t; cin>>t;
while(t--)
{
solv();
}
return 0;
}
G. Ash's Adventures
Problem Author: arsinha
We need to find the count of numbers with $$$3$$$ distinct prime factors between $$$1$$$ to $$$n$$$.
Try using the idea of a sieve.
Generate a sieve with indices till $$$n$$$, and initialise all elements to $$$0$$$. Now start traversing from $$$2$$$ till $$$n$$$, for each index $$$i$$$, check if $$$a_i$$$ is equal to $$$0$$$, if yes it would mean that it is a prime number, hence we can add $$$1$$$ to all $$$a_j$$$ where $$$j$$$ is a multiple of $$$i$$$. This would ensure that by the end of the iterations, $$$a_i$$$ will store the count of distinct prime factors of $$$i$$$. Print all $$$i$$$ for which $$$a_i$$$ is $$$3$$$.
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int sieve[n+10] = {0};
for(int i=2; i<=n; i++){
if(sieve[i]==0){
sieve[i] = 1;
for(int j=2*i; j<=n; j+=i){
sieve[j]++;
}
}
}
for(int i=2; i<=n; i++){
if(sieve[i]==3) cout<<i<<" ";
}
cout<<endl;
return 0;
}
H. Multisource Pandemic
Problem Author: arsinha
The spread of infection replicates breadth-first search
Do a standard breadth-first search while maintaining the count of new houses getting infected on each day. If the count of infected houses is less than the total number of houses after the complete breadth-first search then it implies that some parts of the town are isolated and since the entire town is never infected, the potion is never administered, and all the infected houses die. Else all except the houses infected in the last $$$k$$$ days would die.
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
void solve()
{
int m, n;
cin >> m >> n;
int k;
cin >> k;
char town[m + 2][n + 2];
int total_houses = 0;
memset(town, '.', sizeof(town));
queue<pair<int, int>> source;
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
cin >> town[i][j];
if (town[i][j] != '.')
total_houses++;
if (town[i][j] == 'I')
source.push({i, j});
}
}
vector<int> infected_count;
while (!source.empty())
{
int curr = source.size();
infected_count.push_back(curr);
for (int i = 0; i < curr; i++)
{
pair<int, int> root = source.front();
source.pop();
if (town[root.first + 1][root.second] == 'N')
{
source.push({root.first + 1, root.second});
town[root.first + 1][root.second] = 'I';
}
if (town[root.first - 1][root.second] == 'N')
{
source.push({root.first - 1, root.second});
town[root.first - 1][root.second] = 'I';
}
if (town[root.first][root.second + 1] == 'N')
{
source.push({root.first, root.second + 1});
town[root.first][root.second + 1] = 'I';
}
if (town[root.first][root.second - 1] == 'N')
{
source.push({root.first, root.second - 1});
town[root.first][root.second - 1] = 'I';
}
}
}
int infected_count_sum = accumulate(infected_count.begin(), infected_count.end(), 0);
if (infected_count_sum < total_houses)
{
cout << total_houses - infected_count_sum << endl;
return;
}
int deaths = 0;
for (int i = 0; i < infected_count.size() - k; i++)
{
deaths += infected_count[i];
}
cout << total_houses - deaths << endl;
}
int32_t main()
{
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
solve();
return 0;
}
I. Shadow Hunt
Problem Author: ShruthiK
Try solving using the method of two-pointers.
What can we say about the length of the shadow produced by a given pair of $$$a_l$$$ and $$$a_r$$$ ($$$l$$$ & $$$r$$$ denote the left & right pointers) how does it change upon increasing $$$l$$$ or by decreasing $$$r$$$?
We can solve using the method of two pointers. Initially Let $$$l=0$$$ and $$$r=n-1$$$. If $$$a_r<a_l$$$ then the length of the shadow that the given pair object can produce is $$$a_r+r-l$$$, in which case the length of shadow produced by taking $$$r$$$ as the object will decreases as we increase $$$l$$$ because the x-axis distance will decrease with the height on y-axis being the same. However there is a possibility that we can find a longer shadow by taking $$$l$$$ as the object with a lesser $$$r$$$, so we decrease $$$r$$$ to see if we can get a longer shadow. Similarly if $$$a_l \le a_r$$$ then we increase $$$l$$$. We keep moving $$$r$$$ and $$$l$$$ until $$$r=l$$$ and simultaneously keep track of the overall maximum length as we iterate.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve()
{
ll n;
cin>>n;
ll a[n];
for(ll i=0;i<n;i++) cin>>a[i];
ll x=n-1;
ll l=0,r=n-1;
ll ans=0;
while(r>l)
{
if(a[r]<a[l])
{
ans=max(ans,a[r]+x);
r--;x--;
}
else
{
ans=max(ans,a[l]+x);
l++;
x--;
}
}
cout<<ans<<endl;
}
int main()
{
ll t;
cin>>t;
while ((t--))
{
solve();
}
}
J. Jumbled Names
Problem Author: arsinha
If you are allowed to swap $$$i^{th}$$$ and $$$j^{th}$$$ and $$$j^{th}$$$ and $$$k^{th}$$$ letter then all permutations of $$$i, j, k$$$ are possible.
The same logic works for any number of letters that are connected.
View each index as a node in a graph. Initially, have all the nodes isolated, for all possible swaps, and connect the respective nodes. This will form a collection of connected components. If the swaps have been done within the same component, it is possible to recover back. Otherwise, there is no way to swap nodes that are part of $$$2$$$ different isolated components.
#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
#define int long long
int parent[100000];
int sizes[100000];
int find_set(int v) {
if (v == parent[v])
return v;
return parent[v] = find_set(parent[v]);
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (sizes[a] < sizes[b])
swap(a, b);
parent[b] = a;
sizes[a] += sizes[b];
}
}
void solve()
{
int n;
cin>>n;
int q;
cin>>q;
string s, t;
cin>>s>>t;
vector<pair<int, int>> v(q);
for(int i=0; i<n; i++){
parent[i] = i;
sizes[i] = 1;
}
for(int i=0; i<q; i++){
int x, y;
cin>>x>>y;
union_sets(x, y);
}
for(int i=0; i<n; i++){
int temp = find_set(i);
}
unordered_map<int, vector<int>> roots;
for(int i=0; i<n; i++){
roots[parent[i]].push_back(i);
}
for(auto it = roots.begin(); it != roots.end(); it++){
string a = "";
string b = "";
vector<int> vec = it->second;
for(int i=0; i<vec.size(); i++){
a.push_back(s[vec[i]]);
b.push_back(t[vec[i]]);
}
sort(a.begin(), a.end());
sort(b.begin(), b.end());
if(a != b){
cout<<"NO"<<endl;
return;
}
}
cout<<"YES"<<endl;
return;
}
int32_t main()
{
ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int t = 1;
while(t--)solve();
return 0;
}
K. Package Delivery
Problem Author: Tahir_Sandalwala
He cannot travel each edge more than twice, this means that when he reaches any node $$$v$$$ for the first time, he must deliver packages to all nodes in the subtree rooted at $$$v$$$ and only then return to $$$v$$$.
Given you reach some node with $$$2$$$ children in the tree at a time $$$t$$$, does your decision on which of the two subtrees to cover first depend on $$$t$$$?
Imagine you are at node $$$v$$$ which has children $$$a$$$ and $$$b$$$ at any time $$$t$$$ and you have to make a choice between whether to cover the subtree rooted at $$$a$$$ first or the subtree rooted at $$$b$$$ first. Lets say we cover the subtree rooted at $$$a$$$ first and then at $$$b$$$. It can be shown that the optimal sum of annoyances in the subtree a is given by $$$k_a + imp_a \cdot t$$$, where $$$imp_a$$$ is the sum of importance values of all nodes in the subtree rooted at $$$a$$$ and $$$k_a$$$ is the optimal sum of annoyance if $$$t$$$ were $$$0$$$. After traversing the subtree rooted at $$$a$$$, we return to the root $$$v$$$ at time $$$t + t_1$$$ where $$$t_1 = 2 \cdot t_a$$$ where $$$t_a$$$ is the total sum of edge weights of the subtree rooted at $$$a$$$. Now traversing the subtree rooted at $$$b$$$ leads to an optimal sum of annoyances of $$$k_b + imp_b \cdot (t + t_1) = k_b + imp_b \cdot t + 2 \cdot imp_b \cdot t_a$$$. Hence the total optimal sum of annoyances can be expressed as $$$k_a + k_b + (imp_a + imp_b) \cdot t + 2 \cdot imp_b \cdot t_a$$$. Similarly the optimal sum of annoyances if we covered the subtree rooted at $$$b$$$ first and then $$$a$$$ would be $$$k_a + k_b + (imp_a + imp_b) \cdot t + 2 \cdot imp_a \cdot t_b$$$. On comparing these two expressions we conclude that it would be optimal to traverse $$$a$$$ first if $$$imp_b \cdot t_a > imp_a \cdot t_b$$$ and traverse $$$b$$$ otherwise.
We can solve the problem with two dfs traversals, first to calculate the sum of importance and the sum of edge weights in the subtree of each node and second to explicitly calculate the optimal sum of annoyances by traversing optimally.
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("O3")
#pragma GCC target("avx2")
#include<bits/stdc++.h>
using namespace std;
using namespace chrono;
#define pub push_back
#define pob pop_back
#define ya cout<<"YES\n"
#define na cout<<"NO\n"
#define imp cout<<"Impossible\n"
#define ff first
#define ss second
#define sz(x) ((int)(x).size())
#define all(x) (x).begin(), (x).end()
#define precision(a) {cout << setprecision(a) << fixed;}
#ifndef ONLINE_JUDGE
#define debug(x) cerr << #x <<" "; _print(x); cerr << endl;
#else
#define debug(x);
#endif
typedef long long ll;
typedef long double ld;
typedef vector<int> vi;
typedef vector<char> vc;
typedef vector<double> vd;
typedef vector<ll> vll;
typedef vector<string> vs;
typedef vector<ld> vld;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef map<int,int> mii;
typedef map<ll,ll> mll;
typedef set<int> si;
typedef set<ll> sll;
typedef set<pll> spll;
typedef vector<pair<int,int>> vpi;
typedef vector<pair<ll,ll>> vpll;
typedef tuple<ll,ll,ll> tll;
typedef vector<tll> vtll;
void _print(ll t) {cerr << t;}
void _print(int t) {cerr << t;}
void _print(string t) {cerr << t;}
void _print(char t) {cerr << t;}
void _print(double t) {cerr << t;}
template <class T, class V> void _print(pair <T, V> p) {cerr << "{"; _print(p.ff); cerr << ", "; _print(p.ss); cerr << "}";}
template <class T> void _print(vector <T> v) {cerr << "[ "; for (T i : v) {_print(i); cerr << ", ";} cerr << "]";}
template <class T> void _print(set <T> v) {cerr << "[ "; for (T i : v) {_print(i); cerr << ", ";} cerr << "]";}
template <class T, class V> void _print(map <T, V> v) {cerr << "[ "; for (auto i : v) {_print(i); cerr << ", ";} cerr << "]";}
template <class T> void _print(multiset <T> v) {cerr << "[ "; for (T i : v) {_print(i); cerr << ", ";} cerr << "]";}
template <class T> ostream& operator<<(ostream &os, vector<T> a) { for(auto x:a){ os<<x<<" "; } return os; }
template <class T> ostream& operator<<(ostream &os, set<T> a) { for(auto x:a){ os<<x<<" "; } return os; }
template <class T> ostream& operator<<(ostream &os, multiset<T> a) { for(auto x:a){ os<<x<<" "; } return os; }
template <class T,class Q> ostream& operator<<(ostream &os, pair<T,Q> a) { os<<"| "; os<<a.ff<<", "<<a.ss<<" "; return os<<"|"; }
template<class P,class Q, class T> ostream& operator<<(ostream &os, tuple<P,Q,T> a){ os<<"| "<<(get<0>(a))<<", "<<(get<1>(a))<<", "<<(get<2>(a))<<"|"; return os; }
#include <ext/pb_ds/assoc_container.hpp> // Common file
#include <ext/pb_ds/tree_policy.hpp> // Including tree_order_statistics_node_update
#include <ext/pb_ds/detail/standard_policies.hpp>
using namespace __gnu_pbds;
typedef tree<int,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update> ordered_set;
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
void precomp()
{
}
ll imp_sum[100001], time_sum[100001], where[100001];
ll a[100002];
void dfs(vector<pll> v[], ll pos, ll last)
{
if(v[pos].size()==1 && last!=-1)
{
return;
}
ll child = sz(v[pos])-1;
if(last==-1) child++;
if(child==1)
{
for(auto i:v[pos])
{
if(i.first!=last)
{
dfs(v,i.first,pos);
imp_sum[pos] += imp_sum[i.first];
time_sum[pos] = time_sum[i.first] + 2*i.second;
where[pos] = i.first;
}
}
}
else
{
pll x,y;
ll c=0;
time_sum[pos] = 0;
for(auto i:v[pos])
{
if(i.first!=last)
{
dfs(v,i.first,pos);
imp_sum[pos] += imp_sum[i.first];
time_sum[pos] += time_sum[i.first] + 2*i.second;
if(c) y = {i.first, i.second};
else x = {i.first, i.second};
c++;
}
}
if(imp_sum[x.ff]*x.ss+imp_sum[y.ff]*(time_sum[x.ff]+2*x.ss+y.ss)<imp_sum[y.ff]*y.ss+imp_sum[x.ff]*(time_sum[y.ff]+2*y.ss+x.ss))
{
where[pos] = x.ff;
}
else where[pos] = y.ff;
}
}
ll cur_t = 0;
ll ans = 0;
void dfs2(vector<pll> v[], ll pos, ll last)
{
ans += a[pos]*cur_t;
if(v[pos].size()==1 && last!=-1)
{
return;
}
ll child = sz(v[pos])-1;
if(last==-1) child++;
if(child==1)
{
for(auto i:v[pos])
{
if(i.ff!=last)
{
cur_t += i.ss;
dfs2(v,i.ff,pos);
cur_t += i.ss;
}
}
}
else
{
pll x,y;
for(auto i:v[pos])
{
if(i.ff !=last)
{
if(i.ff==where[pos]) x = i;
else y = i;
}
}
cur_t += x.ss;
dfs2(v,x.ff,pos);
cur_t += x.ss;
cur_t += y.ss;
dfs2(v,y.ff,pos);
cur_t += y.ss;
}
}
void solve()
{
ll n;
cin>>n;
for(ll i=1;i<=n;i++)
{
cin>>a[i];
imp_sum[i] = a[i];
}
a[0]=0;
vector<pll> v[n+1];
for(ll i=0;i<n;i++)
{
ll x,y,z;
cin>>x>>y>>z;
v[x].push_back({y,z});
v[y].push_back({x,z});
}
dfs(v,0,-1);
dfs2(v,0,-1);
cout<<ans<<"\n";
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
#ifndef ONLINE_JUDGE
freopen("Error.txt", "w", stderr);
#endif
ll t=1;
// cin>>t;
auto start1 = high_resolution_clock::now();
precomp();
while(t--)
{
solve();
}
auto stop1 = high_resolution_clock::now();
auto duration = duration_cast<milliseconds>(stop1 - start1);
#ifndef ONLINE_JUDGE
cerr << "Time: " << duration . count() << endl;
#endif
}
L. Shinchan's Painting
Problem Author: Ayman78
How many ways are there when $$$k > 2 \cdot n$$$?
Try using Dynamic Programming to count the number of ways to paint.
Try to include some information about previous colouring in your dp state
The idea of the problem is to paint the wall $$$2$$$ cells at a time from left to right. We can use a $$$2D$$$ $$$dp$$$ which stores the number of regions remaining to create in the wall, and the number of columns left to paint. The $$$dp$$$ state will also store the colours of the previous two cells painted (since the transition will depend upon it).
Let $$$dp[i][j][p]$$$ denote the number of ways to paint the wall of size $$$2 × i$$$, having $$$j$$$ regions, and the previous two cells have colour code $$$p$$$ ($$$p$$$ can take 4 values — corresponding to $$$RR$$$, $$$RB$$$, $$$BB$$$ and $$$BR$$$).
Check the code below for details about $$$dp$$$ transitions.
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1001;
const int K = 2001;
int dp[N][K][4];
const int MOD = 1e9 + 7;
int ways(int n, int k, int state) //0-RR, 1-RB, 2-BR, 3-BB
{
if(n==0)
{
if(k==0)
return 1;
else
return 0;
}
if(k<0)
{
return 0;
}
if(dp[n][k][state]!=-1)
{
return dp[n][k][state];
}
int ans;
if(state==0)
{
ans = (ways(n-1,k,0) + ways(n-1,k-1,1) + ways(n-1,k-1,2) + ways(n-1,k-1,3))%MOD;
}
else if(state==1)
{
ans = (ways(n-1,k,0) + ways(n-1,k,1) + ways(n-1,k-2,2) + ways(n-1,k,3))%MOD;
}
else if(state==2)
{
ans = (ways(n-1,k,0) + ways(n-1,k-2,1) + ways(n-1,k,2) + ways(n-1,k,3))%MOD;
}
else if(state==3)
{
ans = (ways(n-1,k-1,0) + ways(n-1,k-1,1) + ways(n-1,k-1,2) + ways(n-1,k,3))%MOD;
}
dp[n][k][state] = ans;
return ans;
}
void init()
{
for(int i=0; i<N; i++)
{
for(int j=0; j<K; j++)
{
for(int k=0; k<4; k++)
{
dp[i][j][k]=-1;
}
}
}
ways(1000,2000,0);
ways(1000,2000,1);
ways(1000,2000,2);
ways(1000,2000,3);
}
void solve()
{
int n,k;
cin >> n >> k;
if(k>2*n)
{
cout << 0 << "\n";
return;
}
cout << (ways(n-1,k-1,0) + ways(n-1,k-2,1) + ways(n-1,k-2,2) + ways(n-1,k-1,3))%MOD << "\n";
}
int32_t main()
{
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
init();
int t=1;
cin >> t;
while(t--)
{
solve();
}
return 0;
}
M. Tree Jumps
Problem Author: Mantra7
Try to see If Jerry can escape for a given $$$k$$$.
DFS might help to check for all leaf nodes efficiently.
If Jerry can escape with $$$k=k_1$$$, what about all $$$k>k_1$$$?
Let's try to solve this problem for a particular leaf node and a particular value of $$$k$$$. Each leaf node will have a unique path from root to it. Say that path is $$$p$$$ having $$$m$$$ nodes $$$p_1,~p_2,~...,~p_m$$$.
The problem basically reduces to standard DP problem where we need to reach from index $$$1$$$ to index $$$m$$$ and each time we can go from index $$$i$$$ to $$$i+1,~i+2,~...,~i+k$$$, and the goal is to minimise sum of $$$s_{p_i}$$$ over all index $$$i$$$ that we pass through. Here, $$$dp_i$$$ will denote minimum sum to reach index $$$i$$$, $$$dp_i=a_{p_i}+min(dp_{i-k},~dp_{i-k+1},~...,~dp_{i-1})$$$.
This can be done in $$$O(m\cdot k)$$$ if we check previous $$$k$$$ index for each $$$i$$$. But we can store last $$$k$$$ $$$dp$$$ values in a multiset and get minimum in $$$O(\log{}k)$$$. We just have to insert $$$dp_i$$$ in set and remove $$$dp_{i-k}$$$ at each index. So time complexity decreases to $$$O(m\cdot \log{}k)$$$.
Now, we just have to do this for all leaf nodes. It will take too long to calculate the path to each node and do this separately. The trick is to realise we can use DFS and store the path from root to current node in a vector and keep a multiset of $$$dp$$$s of last $$$k$$$ element in the path. So, for each $$$k$$$, we can figure out whether Jerry can escape or not in $$$O(n\cdot \log{}k)$$$.
At the start of DFS, add current node to path and add $$$dp_{cur}$$$ in multiset and remove $$$dp$$$ of $$$k^{th}$$$ last element in path. Use the minimum in set to update $$$dp$$$ of all children of current node. At the end of DFS, do the reverse, add $$$dp$$$ of $$$k^{th}$$$ last element of path in multiset, remove current node from path and remove $$$dp_{cur}$$$ from multiset. This will restore state of path and multiset, so it will be as if we are doing this for each path.
An important thing to realise is that if Jerry can escape with $$$k=k_1$$$ then he can do with all $$$k\ge k_1$$$. So we can binary search on the value of $$$k$$$ to find the smallest that works. Total time complexity is $$$O(n\cdot \log^2{}n)$$$.
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("O3")
#pragma GCC target("avx2")
#include<bits/stdc++.h>
using namespace std;
using namespace chrono;
#define pub push_back
#define pob pop_back
#define ya cout<<"YES\n"
#define na cout<<"NO\n"
#define imp cout<<"Impossible\n"
#define ff first
#define ss second
#define sz(x) ((int)(x).size())
#define all(x) (x).begin(), (x).end()
#define precision(a) {cout << setprecision(a) << fixed;}
#ifndef ONLINE_JUDGE
#define debug(x) cerr << #x <<" "; _print(x); cerr << endl;
#else
#define debug(x);
#endif
typedef long long ll;
typedef long double ld;
typedef vector<int> vi;
typedef vector<char> vc;
typedef vector<double> vd;
typedef vector<ll> vll;
typedef vector<string> vs;
typedef vector<ld> vld;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef map<int,int> mii;
typedef map<ll,ll> mll;
typedef set<int> si;
typedef set<ll> sll;
typedef set<pll> spll;
typedef vector<pair<int,int>> vpi;
typedef vector<pair<ll,ll>> vpll;
typedef tuple<ll,ll,ll> tll;
typedef vector<tll> vtll;
void _print(ll t) {cerr << t;}
void _print(int t) {cerr << t;}
void _print(string t) {cerr << t;}
void _print(char t) {cerr << t;}
void _print(double t) {cerr << t;}
template <class T, class V> void _print(pair <T, V> p) {cerr << "{"; _print(p.ff); cerr << ", "; _print(p.ss); cerr << "}";}
template <class T> void _print(vector <T> v) {cerr << "[ "; for (T i : v) {_print(i); cerr << ", ";} cerr << "]";}
template <class T> void _print(set <T> v) {cerr << "[ "; for (T i : v) {_print(i); cerr << ", ";} cerr << "]";}
template <class T, class V> void _print(map <T, V> v) {cerr << "[ "; for (auto i : v) {_print(i); cerr << ", ";} cerr << "]";}
template <class T> void _print(multiset <T> v) {cerr << "[ "; for (T i : v) {_print(i); cerr << ", ";} cerr << "]";}
template <class T> ostream& operator<<(ostream &os, vector<T> a) { for(auto x:a){ os<<x<<" "; } return os; }
template <class T> ostream& operator<<(ostream &os, set<T> a) { for(auto x:a){ os<<x<<" "; } return os; }
template <class T> ostream& operator<<(ostream &os, multiset<T> a) { for(auto x:a){ os<<x<<" "; } return os; }
template <class T,class Q> ostream& operator<<(ostream &os, pair<T,Q> a) { os<<"| "; os<<a.ff<<", "<<a.ss<<" "; return os<<"|"; }
template<class P,class Q, class T> ostream& operator<<(ostream &os, tuple<P,Q,T> a){ os<<"| "<<(get<0>(a))<<", "<<(get<1>(a))<<", "<<(get<2>(a))<<"|"; return os; }
#include <ext/pb_ds/assoc_container.hpp> // Common file
#include <ext/pb_ds/tree_policy.hpp> // Including tree_order_statistics_node_update
#include <ext/pb_ds/detail/standard_policies.hpp>
using namespace __gnu_pbds;
typedef tree<int,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update> ordered_set;
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
void precomp()
{
}
ll a[100001];
ll dp[100001];
vll path;
multiset<ll> lastk;
ll mx;
ll k;
void dfs(vll v[], ll pos, ll last)
{
path.pub(pos);
lastk.insert(dp[pos]);
if(sz(path)>k+1)
{
lastk.erase(lastk.find(dp[path[sz(path)-k-2]]));
}
if(v[pos].size()==1 && last!=-1)
{
mx = max(mx,dp[pos]);
}
ll mn = *lastk.begin();
for(ll i=0;i<v[pos].size();i++)
{
if(v[pos][i]!=last)
{
dp[v[pos][i]] = mn + a[v[pos][i]];
dfs(v,v[pos][i],pos);
}
}
if(sz(path)>k+1) lastk.insert(dp[path[sz(path)-k-2]]);
lastk.erase(lastk.find(dp[pos]));
path.pop_back();
}
bool check(vll v[], ll jump, ll c)
{
k = jump;
mx = 0;
lastk.clear();
path.clear();
dp[0] = a[0];
dfs(v,0,-1);
return mx<c;
}
void solve()
{
ll n,c;
cin>>n>>c;
for(ll i=0;i<n;i++)
cin>>a[i];
vll v[n];
for(ll i=0;i<n-1;i++)
{
ll u,w;
cin>>u>>w;
u--;w--;
v[u].pub(w);
v[w].pub(u);
}
if(n==2)
{
if(a[0]+a[1]<c)
cout<<"0\n";
else
cout<<"-1\n";
return;
}
if(!check(v,n-2,c))
{
cout<<"-1\n";
return;
}
if(check(v,0,c))
{
cout<<"1\n";
return;
}
ll l = 0;
ll r = n-2;
while(l+1!=r)
{
ll mid = (l+r)/2;
if(check(v,mid,c))
r = mid;
else
l = mid;
}
cout<<r+1<<"\n";
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
#ifndef ONLINE_JUDGE
freopen("Error.txt", "w", stderr);
#endif
ll t=1;
//cin>>t;
auto start1 = high_resolution_clock::now();
precomp();
while(t--)
{
solve();
}
auto stop1 = high_resolution_clock::now();
auto duration = duration_cast<milliseconds>(stop1 - start1);
#ifndef ONLINE_JUDGE
cerr << "Time: " << duration . count() << endl;
#endif
}
N. Time Machine
Problem Author: Chahel
Try to think about how you will solve a smaller sub problem — what’s the maximum number of items you can get when the items you have are a subset of all the items
We will need to use bitmasking to represent the items in consideration for each subproblem and to implement the dynamic programming solution we need to find suitable transition between the states.
To know the maximum number of items that can be bought using a certain set of items, do we really need to check all subsets of that set of items?
This problem is based on DP + Bitmasking. (We use the various bits of a number to represent whether a particular item has been used or not, that is, if the $$$i^{th}$$$ least significant bit is 1, the $$$i^{th}$$$ item has been used; otherwise it hasn't been used)
$$$dp[i]$$$ is a 3-tuple (pair of (pair of ints) and int) storing the maximum prefix of the items needed that can be obtained, the amount of the following needed item that can be obtained (using the items corresponding to the bits of $$$i$$$ that are equal to 1) and the last item that was used in the process of obtaining them.
Thus, we need a total of $$$2^{n}$$$ states corresponding to each of the possible combinations of the $$$n$$$ items that Nobita has. We initialise all states with $$${0,0,-1}$$$.
To transition efficiently, when we have calculated the value of the state $$$dp[i]$$$, we go over the bits of $$$i$$$ that are equal to zero and update the value of the state, corresponding to exactly one of those bits being one along with the other non zero bits of $$$i$$$ being non zero, accordingly.
The code snippet corresponding to the above transition is presented here:
for (int j = 0; j < n; j++){
if ((i & (1<<j)) == 0){
if (dp[i].first.first == m)
dp[i|(1<<j)] = {{dp[i].first.first, 0}, j};
else if (a[j] + dp[i].first.second < b[dp[i].first.first])
dp[i|(1<<j)] = max({{dp[i].first.first, a[j] + dp[i].first.second}, j}, dp[i|(1<<j)]);
else
dp[i|(1<<j)] = max({{dp[i].first.first + 1, 0}, j}, dp[i|(1<<j)]);
}
}
Thus, each transition takes $$$O(n)$$$ operations. Hence, the overall time complexity of the author's solution is $$$O(t \cdot n \cdot 2^{n})$$$. We have also allowed solutions that have a time complexity of $$$O(t \cdot (3^{n} + n \cdot 2^{n}))$$$, which go over all subsets of each state $$$i$$$. However, unoptimised $$$O(t \cdot m \cdot 3^{n})$$$ or worse solutions (that require more than $$$10^{9}$$$ operations) have not been allowed to pass.
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false); cin.tie(0);
int t;
cin >> t;
while (t--) {
//taking the items Nobita has as input
int n;
cin >> n;
vector<string> Nobita_has(n);
vector<long long int> a(n);
for (int i = 0; i < n; i++)
cin >> Nobita_has[i] >> a[i];
//taking the items Nobita needs as input
int m;
cin>>m;
vector<string> Nobita_needs(m);
vector<long long int> b(m);
for (int i = 0; i < m; i++)
cin >> Nobita_needs[i] >> b[i];
vector<pair<pair<int,long long int>,int>> dp((1<<n),{{0,0},-1});
for (int i = 0; i < (1<<n); i++){
for (int j = 0; j < n; j++){
if ((i & (1<<j)) == 0){
if (dp[i].first.first == m)
dp[i|(1<<j)] = {{dp[i].first.first, 0}, j};
else if (a[j] + dp[i].first.second < b[dp[i].first.first])
dp[i|(1<<j)] = max({{dp[i].first.first, a[j] + dp[i].first.second}, j}, dp[i|(1<<j)]);
else
dp[i|(1<<j)] = max({{dp[i].first.first + 1, 0}, j}, dp[i|(1<<j)]);
}
}
}
if (dp[(1<<n)-1].first.first != m){
cout<<"NO\n";
continue;
}
cout<<"YES\n";
vector<int> ans[m];
int mask = (1<<n)-1;
while (mask > 0){
if (dp[mask].first.second == 0)
ans[dp[mask].first.first - 1].push_back(dp[mask].second);
else
ans[dp[mask].first.first].push_back(dp[mask].second);
mask = mask ^ (1<<dp[mask].second);
}
for (int i = 0; i < m; i++){
cout << Nobita_needs[i] << " = ";
for (int j = 0; j + 1 < ans[i].size(); j++){
cout << Nobita_has[ans[i][j]];
if (j != ans[i].size() - 1)
cout << " + ";
}
cout << Nobita_has[ans[i][ans[i].size()-1]] << endl;
}
}
return 0;
}









