405A - Переключение гравитации
Заметим, что в конечном расположении все высоты столбиков расположены в неубывающем порядке. Также, количество столбиков каждой высоты остаётся неизменным. Это означает, что ответом является упорядоченная последовательность данных высот столбиков.
Сложность решения: O(n), так как можно упорядочить подсчётом.
405B - Эффект домино
Если самая первая толкнутая доминошка слева была толкнута влево на позиции l, все доминошки на префиксе [1;l] падают, иначе пусть l будет 0. Аналогично, если самая последняя толкнутая доминошка была толкнута направо на позиции r, все доминошки на суффиксе [r;n] падают, иначе пусть r будет n + 1. Теперь, на отрезке (l;r) остаются вертикально стоящие доминошки, а также блоки домино, поддерживающиеся одинаковыми силами с обеих сторон.
Когда доминошка на позиции p на отрезке (l, r) остаётся стоять вертикально? В одном случае, её не толкает ни одна другая доминошка. Это можно легко проверить, посмотрев на ближайшие к p толкнутые доминошки (с обеих сторон). Она была затронута другими домино, если самая близкая толкнутая доминошка слева была толкнута направо и самая близкая толкнутая доминошка справа была толкнута влево. Допустим, эти доминошки находятся на позициях x и y, x < p < y. Тогда, единственная возможность для доминошки остаться вертикально тогда, когда она находится в центре блока [x;y], что можно проверить выражением 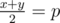 .
.
Сложность решения: O(n) / O(n2), что зависит от реализации.
406A - Необычное произведение
Если записать в виде формулы искомое произведение в задаче, получаем

Допустим, что i ≠ j. Тогда сумма содержит слагаемые AijAji и AjiAij. Так как сумма всегда берётся по модулю 2, вместе эти слагаемые дают 0 к сумме. Из этого следует, что выражение всегда равняется сумме битов на диагонали:
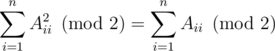
Теперь, каждый запрос типа 1 и 2 меняет значение ровно одного элемента на диагонали. Поэтому мы можем посчитать необычное произведение изначальной матрицы, и после каждого запроса типа 1 и 2 менять его значение на противоположное.
Сложность решения: O(n + q), если не брать во внимание ввод... :)
406B - Игрушечная сумма
Определим для числа k его симметричное число как s + 1 - k. Так как в задаче s чётное число, k ≠ s - k.
Заметим, что (k - 1) + (s + 1 - k) = s, т.е., сумма числа и его симметричного всегда равно s. Будем обрабатывать все числа x множества X по порядку. Различаем два случая:
- Если симметричное x не принадлежит X, добавим его к Y. Оба числа дают одинаковые значения к соответствующим суммам: x - 1 = s - (s + 1 - x).
- Симметричное x принадлежит X. Тогда возьмём любое y такое, что ни y, ни симметричное y не принадлежат X, и добавим их к Y. Обе пары дают одинаковые значения к соответствующим суммам, а именно s.
Как доказать, что во втором случае мы всегда сможем найти такое y? Пусть количество симметричных пар, которые были обработаны в первом случае, равно a, тогда остаются 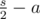 других пар. Среди них, для
других пар. Среди них, для 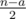 пар оба числа принадлежат X, а для других
пар оба числа принадлежат X, а для других 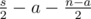 пар никакие из чисел не принадлежат X. Чтобы выбрать такое что количество пар для Y, как и в X, должно выполняться
пар никакие из чисел не принадлежат X. Чтобы выбрать такое что количество пар для Y, как и в X, должно выполняться
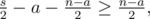
что равносильно 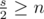 , как и дано в условии.
, как и дано в условии.
Сложность решения: O(s) / O(n).
406C - Разрез графа
Можно доказать, что только графы с нечётным количеством рёбер нельзя разбить на пути длины 2. Мы построим рекурсивную функцию, решающую задачу, которая и будет служить доказательством этого утверждения.
Функция partition(v) будет работать на незаблокированных рёбрах. Она разбивает компоненту вершины v, связную по незаблокированным рёбрам, на пути длины 2. Если компонента имеет нечётное количество рёбер, функция разобьёт все рёбра компоненты, кроме одного ребра (u, v); тогда функция вернёт вершину u, ожидая, что предыдущий вызов функции присвоит это ребро какому-нибудь пути.
Функция работает следующим образом: найдём все вершины, соседние с v по незаблокированным рёбрам, назовём это множество adjacent. Далее заблокируем все рёбра из этих вершин в v. Для каждой u в adjacent, вызовем partition(u). Допустим, что вызов partition(u) вернул вершину w. Это значит, что мы можем присвоить её в путь (v, u, w). Иначе, если partition(u) ничего не вернул, добавим u к unpaired, потому что ребро (v, u) ещё не присвоено ни одному пути. Мы можем объединить в путь любые две вершины этого множества u, w в один путь (u, v, w). Спарим как можно больше таких вершин в любом порядке. Если из этого множества осталась только одна вершина, u, то функция вернёт u. В противном случае функция ничего не возвращает.
Функцию можно реализовать всего одним DFS:
partition(v) :
adjacent = { u | not blocked[(u,v)] }
for(u : adjacent)
blocked[(u,v)] = true
unpaired = {}
for(u : adjacent)
int w = partition(u)
if(w = 0)
add(unpaired, u)
else
print(v,u,w)
while(size(unpaired) >= 2)
int u = pop(unpaired)
int w = pop(unpaired)
print(u,v,w)
if(not empty(unpaired))
return pop(unpaired)
else
return 0
Сложность решения: O(n + m).
406D - Скалолазание
Заметим, что каждый путь скалолаза выпуклый в любом случае. Проведём пути из всех скал до последней скалы. Тогда эти пути образуют дерево с «корнем» в вершине последней скалы. Мы можем применить алгоритм Грэхема справа налево, чтобы найти рёбра этого дерева. Каждое удаление и добавление в стеке соответствует ровно одному ребру в дереве.

Теперь несложно видеть, что для каждой команды скалолазов, нам нужно найти номер наименьшего общего предка для соответствующей пары вершин в дереве. Так как размер дерева равен n, каждый запрос обрабатывается за  .
.
Сложность решения:  .
.
406E - Тройки Хемминга
Давайте рассмотрим хэммингов граф из всех различных 2n строк, где каждые две строки соединены ребром длины, равному расстоянию Хэмминга между этими строками. Мы можем заметить, что этот граф обладает годным свойством: если упорядочить все вершины циклически по правильному 2n-угольнику со стороной длины 1, расстояние Хэмминга для каждых двух строк равняется длине кратчайшего пути между этими вершинами на периметре этого многоугольника.
Например, на рисунке изображён такой граф для n = 3. Серые рёбра имеют длину 1, оранжевые рёбра имеют длину 2, синие рёбра имеют длину 3. Это равняется соответствующему расстоянию Хэмминга.

Теперь, мы можем преобразовать каждую строку, закодированную парой чисел (s, f), в целое число (f + 1)·n - s. Новые числа будут среди 0, 1, ..., 2n - 1 и соотноситься с тем же циклическим порядком на периметре многоугольника. Данные строки переходят в какой-то набор вершин. Теперь нам нужно найти количество треугольников (возможно, дегенерированных) с наибольшим периметром в этом подграфе. Далее будет полезно упорядочить преобразованные числа.
Для начала, можно попробовать понять, каким может быть этот периметр. Если существует такой диаметр в полном графе, что все данные точки находятся по одну сторону диаметра, периметр будет равен 2d, где d является значением самого длинного ребра:
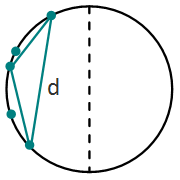
Тогда любой треугольник с двумя вершинами на этом ребре и третьим в любой из остальных точек будет иметь наибольший периметр. Так как числа упорядочены, самое длинное ребро в этом случае будет образовано двумя циклически рядом стоящими элементами, что не трудно найти.
Если для любого диаметра это не выполняется, тогда наибольший периметр равен 2n. Это можно доказать, взяв две различных точки a, b, и проведя два диаметра из этих точек как концов; так как это не предыдущий случай, должна быть третья точка c в месте, где периметр треугольника a, b, c равняется 2n.
Самая хитрая часть и есть посчитать тройки в этом случае. Мы делаем это, работая с диаметром (0, n). Всего может быть несколько случаев:
- Наибольший треугольник содержит обе вершины 0 и n. Это простой случай: с любой другой вершиной как третьей такой треугольник имеет периметр 2n.
- Наибольший треугольник содержит вершину 0, но не n. Тогда вторая вершина должна находится на отрезке [0, n), а третья на отрезке (n + 1, 2n - 1], и расстояние по часовой стрелке между второй и третьей вершинами не должно превышать n (в противном случае периметр треугольника был бы меньше, чем 2n). Мы считаем количество таких троек, двигая два указателя (по одному на каждый из этих отрезков). Для каждого указателя в первом отрезке, все точки, начиная с n + 1 до второго указателя образуют наибольший треугольник. Аналогично мы решаем случай, когда треугольник содержит n, но не 0.
- Наибольший треугольник не содержит ни 0, ни n как вершины. Тогда одна вершина треугольника должна находится на одной стороне диаметра (0, n), а две остальные на другой стороне. Чтобы посчитать их, будем двигать указатель на первую вершину на одной стороне, скажем, (0, n); обозначим диаметрально противоположную вершину за x. Тогда вторая вершина может быть любой на отрезке [n + 1, s], а третья может быть любой на [s, 2n - 1]. Количество этих точек легко посчитать, используя частичные суммы на круге. Заметьте, что s может быть как второй, так и третьей вершиной одновременно (строки могут повторяться). Тогда мы двигаем этот указатель через все вершины одной стороны и обновляем ответ. Аналогично мы решаем случай, когда первая вершина на второй стороне, а обе других на противоположной.
Остаётся только быть осторожными с формулами в каждом случае.
Сложность решения: 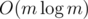 из-за сортировки.
из-за сортировки.
Post Scriptum
Какими были ваши решения? Не стесняйтесь поделиться любыми решениями или мыслями! Например, было ли в DivI E решение, проще авторского?











Yes, there was a simpler solution to Div1 E :D. I'm pretty sure the idea's the same, but I find its phrasing really simple to understand.
Imagine you picked 3 strings and want to express their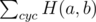 . Each of N bits contributes to the Hamming sum with 2 if one of the chosen strings has a different bit at that position than the other two and 0 otherwise. That means the Hamming distance is 2N - K, where K is the number of positions where the 3 strings have the same bit (all 0 or all 1).
. Each of N bits contributes to the Hamming sum with 2 if one of the chosen strings has a different bit at that position than the other two and 0 otherwise. That means the Hamming distance is 2N - K, where K is the number of positions where the 3 strings have the same bit (all 0 or all 1).
We'll call si the type of a string. Let's fix a type t now.
Let's first look at the case when a, b are of type t and c is of type 1 - t. W.l.o.g. fa ≤ fb. If fa ≤ fc ≤ fb, the maximum value of the Hamming sum is 2N — and it can't be maximized any further. The number of triples for given t and c is the number of pairs {a, b} such that sa ≤ sc ≤ sb and their sum over all c (for given t) can be found using 2 pointers on a sorted array.
What if there's no triple {a, b, c} for which fa ≤ fc ≤ fb? It means that values fc of all c are either all (strictly) below the smallest fa or all above the largest fb. W.l.o.g. assume the first case. In order to minimize the number of positions with identical bits (the ones between the fc + 1-st and fa-th), we need to pick the largest fc and the smallest fa; fb can be then picked however we want.
There is a third case where all 3 strings are of the same type t. W.l.o.g. assume fa ≤ fb ≤ fc. It's obvious that there are fc - fa positions with non-identical bits, and so we want to maximize fc - fa. This is the most easily done by picking the largest fa and the smallest fc; once again, fb falls into the abyss of oblivion :D
Notice that each case leads to one value of cyclic Hamming distance for all triples counted in it. Also, all cases are disjoint — we can't count a triple in 2 cases.
The rest is just about treating all cases (we try both t in the same way), writing the formulas for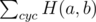 and for computing the number of triples — watch out for equal fi — and picking just the sum of cases with the maximum Hamming distance. More on that in the code: 6127737. Time complexity: also
and for computing the number of triples — watch out for equal fi — and picking just the sum of cases with the maximum Hamming distance. More on that in the code: 6127737. Time complexity: also 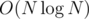 .
.
Hi gen, regarding your solution for Graph Cutting Problem, I tried to understand the logic of partition function which I could not understand clearly, I got the idea in somewhat high level fashion, But I could not implement it. I implement your function as it as you have provided, your partition function always returns 0.
So please post your code for this problem so that I can learn from it.
Here is my code http://ideone.com/Ny9PjL
Sorry for the trouble, I corrected the mistake. Here is my code, but there are some redundant structures, as I now realize.
sorry to trouble you again, but with this modification too, I am getting TLE on a large test case http://codeforces.net/contest/406/submission/6127948. I feel like my code is going into cycles :(
This test contains a full graph with 444 vertices, you can try it locally. Our Java solution also works slower than average on this test, since it makes a new
ArrayListin each DFS call. Maybe you have a similar problem, since you make two vectors in each call.I feel that something wrong with the 406C — Graph Cutting solution: print(u,v,w) where u and w are adjacent to adjacent vertex to current v that is why they are not adjacent with v directly, aren't they? That is why my direct realization of algorithm, which is written here achives wa1
I think that there should be smth like
rather than
Could you explain me, please, am I wrong?
Thanks, my wrong. It should be
If the component was partitioned completely, the edge (v, u) is left unpaired. Otherwise we make a path (v, u, w), as you suggested.
Is it just me here think that Div2 D is easier than C ? :))
it is only you :P
Thanks for the round! I thought Div1 C in particular was a nice problem. Here's my solution:
It is clear that the total number of edges must be even. Our goal is essentially to direct each edge in a way that gives each vertex an even indegree. Then we can form the paths by taking pairs of edges that point to the same vertex.
To do this, find any spanning tree in the graph. Then, direct all edges not in the tree arbitrarily. We will use the spanning tree to "fix" the parities of the indegrees of each node.
However, this is easy to accomplish with tree DFS. For each node, we run the DFS on all of its children and then direct the node-parent edge so that the node's total indegree is even. The root node will automatically have even indegree if the total number of edges is even.
What is meant by Non-blocked edges in Div1 C?
this mean the edges we have not alredy blocked. It is quite clear written in pseudocode: we are blocking all adjacent and still unblocked to current vertex edges, before before doing dfs with their ends.
В "B" (Div.2) задании регулярными выражениями (regexp) проходим по строке и изменяем — снимаем двинутые домино, оставляем недвинутые, ответ — длина строки. Perl — 6130110.
Div 1 A is a very nice problem !!!
Can someone explain how LCA is used in the solution for problem D?
Take, for example, nodes 5 and 7 from the picture in the solution. LCA(5,7) = 6, but the answer is actually 7...
Can someony clarify this?
The edges are not oriented to the higher peak, because the climbers don't go to the higher peak. They're oriented to the right, because the climbers always go to the right. LCA(5,7)=7.
Ahhhh, I get it. I hadn't read the part that says "with the root at the top of the rightmost hill".
Thanks!
Can someone provide the demonstration for problem C Div 1
Простите, я достаточно еще "новичок здесь, но хочу высказаться по понравившейся мне задаче. Возможно, меня поправят, за что буду признателен.
1) Просматриваем массив с обеих концов на предмет серии полностью упавших доминошек и "валим" их, если нашлись, это я с автором комментария согласен.
2) Далее, согласно условия, у нас будут только пары R.. ..L c любым количеством доминошек между ними. Просматриваем массив на оставшемся отрезке слева направо, если нашли R(пусть в позиции r), то впереди ищем L (пусть в позиции l), "валим" весь отрезок и восстанавливаем позицию (r+l)/2, если она выражается целым числом.
3) Просматриваем весь массив на предмет оставшихся доминошек.
Итого сложность O(n), не больше.
I solve Div.1 E problem by list all the possible conditions. And I also find out many people pass this problem by similar idea. Xellos has explained the idea at length. By the way,there are many details in equal strings. Nice problem any away!