This Thursday (27.3.2014), the first (theoretical) day of the national round of Slovak Olympiad in Informatics took place (and I appeared there, much to everyone's surprise :D). So, I bring you the problems and solutions. The second, practical day, can be found here.

UPD: The original version of the problems and solutions is up. In case you were curious, final results. In Slovak, of course :D

You can have fun trying to find CF handles of some contestants :D

UPD2: The contest is in Gym now (both days merged into 1 contest, one problem omitted due to being too theoretical). It only took a year!

Problems: 1 2 3

Solutions: 1 2 3

Problem 1: Mr. Buridan and coffee shops.

Buridan's donkey is a famous philosophical mind experiment. Imagine putting a hungry donkey in front of two identical heaps of hay. The donkey would like to eat, but as the situation's perfectly symmetric, it can't decide whether to pick the left or right heap. And so, it stays in place until it dies of hunger.

Little David is still trying to find a place to live in Manhattan. Besides other stuff, he likes visiting coffee shops. But he just realized that he's in the same danger as Buridan's donkey: if some 2 coffee shops were equally distant from his flat, it's possible that he couldn't decide which one to visit and that wouldn't end well...

For simplicity, we'll picture Manhattan as a square grid, where we can only move in the 4 basic directions. There are coffee shops at some grid points and David also wants to live at some grid point (possibly containing a coffee shop).

The input contains a map of Manhattan. For every intersection (grid point), find out if little David can live there — e.g. if all coffee shops are at different distances from there.

Input format

The first line of the input contains an integer N — dimension of the Manhattan square grid. The grid is formed by N vertical and N horizontal streets, so we have N² intersections (grid points). The rest of the input contains N lines of N integers each: 0 if there's no coffee shop at that point and 1 if there is one.

Output format

Print N lines of N characters each: A if little David can live at that point and N otherwise.

Samples

Input

5
1 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 1
0 0 0 0 0

Output

A A A A A
A A A A N
N N N N A
A A A A A
A A A A A

Input

3
1 0 1
0 0 0
1 0 1

Output

N N N
N N N
N N N

Input

2
0 1
0 0

Output

A A
A A

Problem 2: Tug of war.

In Hillside Village, a traditional tug of war tournament takes place. Since there's no horizontal field in the whole village, the game is played on a slope of a hill. The hill's steepness is represented by a coefficient q > 1. There are N players starting in the tournament, numbered 1 to N from youngest to oldest. Player number i has strength s_i.

At the start of tournament, all players are active. The tournament consists of several matches. All active players play in a match. At the start of a match, they split into 2 teams: the upper team (on the top of the hill) consists of the K oldest players; the lower team consists of the rest. A team's strength is the sum of strengths of all its players. The upper team has an obvious disadvantage; the win iff their strength is strictly larger than q times the lower team's strength. The tournament ends as soon as the upper team wins.

After each match, one player stops being active. The natives noticed that it's always either the youngest active player (who has to go home) or the oldest active player (who visits the buffet). The value of K remains unchanged, so if the oldest player leaves, then the oldest player of the lower team automatically switches teams. (Notice that if such a player doesn't exist, then the tournament would end anyway.)

The input contains the number of players N, their strengths s_1..N, the coefficient of hill's steepness q and the size of the upper team K. Write a program which computes the maximum number of matches that could be played. In other words, it's supposed to find such an order of leaving players, for which the upper team wins for the first time as late as possible.

Input and output format

The first line of the input contains numbers N, K (1 ≤ K ≤ N) and a real number q. You may assume that all calculations involving real numbers are precise.

The next line contains N positive integers small enough to fit into common integer variables: s₁ to s_N.

Print a single number — the maximum possible number of played matches.

Samples

Input

5 2 1.01
40 70 1000 30 20

Output

4

Input

12 7 2.0
2 4 9 5 3 3 4 8 8 6 1 6

Output

4

Problem 3: Computers from outer space.

There's an extensive text describing this type of problems. A short outline:

Aliens have given us a special type of computers (called KSP for short). These computers can solve hard problems in (gasp) O(1) time! There are 2 types: a hall computer, which takes a whole hall and despite, the short computation time, makes setting it up so annoying that it can only be run once for one input; suitcase computers, on the other hand, can be run multiple times without any problems. You're presented with problems which require using these computers to achieve polynomial time complexity; beyond that, the exact complexity of your program does not matter at all. They also don't specify the format of input/output or anything — what matters is only the idea. They usually require modifying the given graph by adding/removing edges/vertices.

Subtask A)

We have a hall KSP which decides whether there's a Hamiltonian path in a given graph containing a given edge. In other words, you can make 1 call to a function bool path_with_edge(n,E,u,v), where the arguments are number of vertices of the graph, the list of its edges and (existing) edge (u, v). Your program ends by calling this function.

Given a simple undirected graph G, write a program which decides whether it contains a Hamiltonian path.

Subtask B)

We're given a suitcase KSP which decides whether there's a Hamiltonian path in a given graph — we can call a function bool path(n,E) as much as we want.

Given a simple undirected graph G which contains a Hamiltonian path, construct one such path. In this subtask, you're trying to minimize the number of calls of path().

Subtask C)

We're given a hall KSP, which (again) decides whether there's a Hamiltonian path in a given graph with function bool path(n,E). You can only use this function once and your program ends by calling it.

Given a directed graph G, write a program which decides whether it contains a directed Hamiltonian path.

Solutions

Problem 1 (code)

Let's pick a grid point and look at the distances of all coffee shops. They must all be in the range [0, 2(N - 1)]. Therefore, if the number of coffee shops K is  > 2(N - 1), then there must be 2 coffee shops at the same distance, by Dirichlet's principle — and that holds for all grid points, so we can print all "N"s.

Otherwise, K is O(N). Let's show a way to solve the problem in O(N² + K²).

Consider a rectangle N × M whose 2 opposite corners contain coffee shops. Which points inside this rectangle will have equal distances from these 2 shops?

If the distance of the 2 shops (N + M - 2) is odd, then there are no such points, because the sum of distances of our point P from those 2 shops is always equal to N + M - 2, which is  ≠ 2d. Otherwise, it's a diagonal — w.l.o.g. if the top left and bottom right corner contain coffee shops, then all points on any diagonal that runs from up right to down left have the same distances from each shop, and moving down/right to another diagonal increases the distance from the top left shop and decreases the one from the bottom right shop.

We just need to find the border points of this diagonal; then, we can mark one of these points (the top left/right one) as "+1 diagonal starts here" and the other (they could coincide if the diagonal is formed by just 1 point) as "+1 diagonal ends here".

They can be found by considering all cases for which side of the rectangle they can be on — in our w.l.o.g. case, one of them is on the left or the bottom side (the bottom left corner is also possible) and the other on the right/top side. If an endpoint of a diagonal lies on the top side, then the distances from both shops x and N + M - 2 - x must be equal for 0 ≤ x < M (actually, x > 0 for distinct shops, e.g. N + M > 2), so if 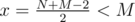, then (0, x) is an endpoint of the diagonal. Analogously for other sides.

What about points outside the rectangle? The difference of distances of the 2 shops won't change by moving closer to the rectangle, so we can mark the border points of the diagonal as "to the left is also N" or "to the right is also N" or "up is also N" or "down is also N" (depending on the sides of the rectangle that they're on). This also means that any other points outside the rectangle can't be "N" for this pair of shops. Watch out, these rules also hold when combined — if a corner is part of the equal diagonal, then it causes a whole rectangle to consist of "N"s. Also, rules over several pairs of shops don't combine.

We can just try all pairs of shops, find the diagonal borders and note the O(1) pieces of information.

Then, we'll convert this implicit form of the output array into an explicit one. A point is on some N-diagonal of some rectangle if more N-diagonals start before it/on it than end before it, so this can be found out just by traversing all diagonals (separately all up left — down right ones and all up right — down left ones) and counting these numbers. Also, a point is N if there's a point marked as "to the left is also N" to its right, and analogously for "right", "up" and "down" (for combinations of 2 rules, it's sufficient to i.e. have a point marked as "to the left+bottom is also N" to its top right!). This can also be processed by traversing all rows and columns in both directions (the combined rules can be processed by traversing the whole table). And any point not marked as "N" is "A".

Time complexity is therefore O(N²); same with memory.

Problem 2 (code)

This is just simplified NEERC 2012: Sultan's pearls, but with a better story. Seriously, tug of war on a hill? :D

First observation: the remaining players always form an interval s_l to s_r.

Second observation: If we fix the right border r of the interval (e.g. the size of the upper team), there's some minimum index i ≥ 0 such that the lower team wins iff l ≤ i. It's obvious — the larger i, the smaller the lower team and the smaller its strength. Also, obviously i ≤ r - K, because the lower team would not have any players otherwise and would lose instantly (when l = r - K + 1).

After each match, l is incremented or r decremented. We can see that the greedy strategy is optimal: if there's a sequence that leads to the lower team winning the match for [l₀, r₀], then the strategy "first decrease r from N to r₀, then increase l from 1 to l₀" — any other strategy will have to win some match with r₀ ≤ r ≤ N and match [l₀, r₀], so

just make the l for those matches as large as possible — it can't make the situation worse.

The possibility of the lower team winning match [l, r] can be checked using prefix sums (S[k] is the sum of s₁ to s_k). We'll just rewrite the condition

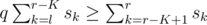
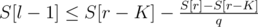
Now, we can limit ourselves to r greater than the largest r_x for which not even the match with l = 1 can be won. If the last won match for a fixed r > r_x is [l, r], then it gives the answer N - r + l, which is maximal for l = i (it can't be larger, because the next match can't be won). Therefore, we need to find the maximum of N - r + i_r over all r > r_x.

This can be solved using 2 pointers for r and l. We'll iterate from r = r_x + 1 to r = N. The second pointer will be at l such that N - r + l is  ≥  to the maximum answer found so far — that means if we increment r, we must increment l. Also, we'll try to push the second pointer (l) as far right as possible — if [l, r] can be won, then we can increment it.

It works because decreasing l at any time won't give us a better answer and we'll be able to get to the same states as without doing so. This way, l can only increase, so the total time complexity is O(N). Memory is also O(N).

Problem 3 (code: maybe TBD)

Subtask A)

Add 2 vertices u and v. Connect v to all vertices except itself. Now, any Hamiltonian path in so created graph G' consists of edges u - v, v - w (for some 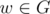) and a H. path in G, which starts at w, and any Hamiltonian path in G can be extended by vertices v and u. Also, any H. path in G' must contain edge u - v, so the existence of a Hamiltonian path in G is equivalent to existence of a H. path using edge u - v in G'.

Subtask B)

Suppose that we chose a subset 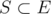. If we called path(n,E-S) and received True, we know that there's a Hamiltonian path in graph G' = (n, E \ S).

We can use the fact that there are at most 2 edges of a H. path incident on any vertex. As long as there's some vertex v with degree at least 3, we can split the set E_v of edges incident on v into 3 non-empty subsets S₁, S₂, S₃ with sizes around 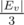and call path(n,E-S_1-S_2), path(n,E-S_2-S_3) and path(n,E-S_3-S_1); at least one of these calls will return True and we know that removing the corresponding subset S_i from E will give us a graph with less edges and containing a Hamiltonian path. When we can no longer do this, our graph is a cycle or a path, from which we can easily reconstruct a H. path.

There are 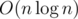calls to path(). More precisely, for any v, just 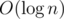calls corresponding to E_v can be made. Notice that |E_v| ≤ n; each call multiplies |E_v| by approximately , so there are around 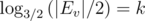(smallest k such that 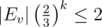calls, and 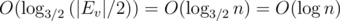, since changing the base of the logarithm doesn't affect the asymptotic.

Subtask C)

We only need to force a path to alternate between edges going inside a vertex and outside it — if we find an undirected path which does so, we can then direct it in the right way.

Let's create a new, undirected graph G'. Vertex v in G will correspond to a pair of vertices v₁ and v₂, connected by an edge. Plus, an edge u -  > v in G will correspond to an edge u₂ -  > v₁ in G' — vertex v₁ will correspond to edges into v and v₂ to edges out of v.

Let's add 2 more vertices x and y to G', x connected to all v₁-s and y to all v₂-s, and 2 more vertices w and z, connected to x and y respectively. This forces any Hamiltonian path in G' to start and end at w and z.

Also, let's split edges v₁ - v₂ into v₁ - v₃ and v₂ - v₃ for all v (v₃ are new vertices). Now, any H. path in G must have 2 edges incident on any vertex except its ends w and z; for v₃-s, these must be v₁ - v₃ and v₂ - v₃, so for v₁-s and v₂-s, one edge must be the one connecting this v_i to v₃. Therefore, a Hamiltonian path must get to v₁ by some edge that went into v, then move through v₃ to v₂ and exit it through some edge that went out of v, never to visit v₁, v₂ or v₃ again (but visiting each of them exactly once, which is like visiting v exactly once); that must hold for all v.

From this, we see that a H. path in G can be converted into a H. path in G' (moving through vertices as described, plus connecting w - x -  and  - y - z to its ends). Also, a H. path in G' can be converted into a H. path in G in the same way, so there's an equivalence between existance of an undirected Hamiltonian path in G' and a directed one in G, and we only need to call path() on G'.