This is a continuation of my blog post about day 1.

You can find the constraints and samples in the original problem statements (in Slovak, but that doesn't matter with numbers :D).

UPD2: The contest is in Gym now (both days merged into 1 contest, one problem omitted due to being too theoretical). It only took a year!

Problems: 4 5 6

Solutions: 4 5 6

Problem 4: Up and down

(original time limit: 300 ms)

Baška had a sequence of N integers from the range [0, M]. For every 2 consecutive elements of the sequence, she wrote down  < ,  =  or  >  depending on the earlier one of them being lesser, equal or greater than the later one. For example, as for a sequence (3, 1, 7, 7, 4) we have 3 > 1 < 7 = 7 > 4, Baška would've written down  >  <  =  > .

Olívia doesn't know Baška's original sequence. She only knows N, M and the sequence of characters that Baška wrote down. Now, she'd like to reconstruct Baška's sequence — as far as possible.

You can get a partial score by writing a program which reconstructs any correct sequence (if it exists). In order to get full score, your program needs to find the sequence whose sum is minimal.

Input and output format

The input consists of 2 lines. The first contains integers N and M; the second contains a string of N - 1 characters [ <  =  > ] — the sequence that Baška wrote down.

Print one line containing your reconstruction of Baška's original sequence — N space-separated integers. If no such sequence exists, print N times  - 1.

Problem 5: Balanced strings

(original time limit: 1500 ms)

We call a string balanced if all its characters (those which occur in it at least once) occur in it an equal number of times. For example, aaaaa, badcx, bbaaab are balanced strings. However, abacb isn't a balanced string.

Given a string, find its longest (continuous) balanced substring.

The substring we're looking for doesn't have to contain all characters which occur in the original string. For example, the correct answer for cbababac is the substring bababa.

Input and output format

The input consists of a single string of lowercase letters of English alphabet. The string has length N and the characters are indexed from 0 to N - 1.

Print a single line containing two space-separated integers: indices of the character by which the substring we're looking for starts and the one by which it ends. If there are multiple optimal solutions, find the one that starts the earliest.

Problem 6: ACGT

(original time limit: 3000 ms)

Usámec is trying to construct a genome from DNA fragments. A DNA fragment is a sequence of letters [ACGT]. Usámec has found N fragments already, let's denote them as F_1..N. There are also M rules describing which fragments can follow directly after which ones.

Constructing a DNA

DNA is a sequence of fragments F_ai (for some sequence 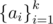; 1 ≤ a_i ≤ N) such that for every i > 1, the a_i-th fragment can follow after the a_i - 1-st one. We construct the DNA by concatenating those fragments and obtain a string of letters [ACGT] as a result.

Distance of strings

We can modify a string in steps, where each step is one of these 3 types of changes: adding a character into the string, removing or changing one character in the string. We define the distance of strings p and q as the smallest number of steps we need to make in p to turn it into q (clearly, any string has distance 0 from itself). For example, strings ATTA and AGA have distance 2 — we need to remove 1 T and change the other into G.

You're given some DNA fragments and rules that describe which fragment can follow after which one. You're also given a target DNA string r, a very small non-negative integer d and indices of 2 fragments, u and v (u ≠ v). You should write a program that finds one possible sequence of fragments that starts with fragment u, ends with fragment v and the DNA that's constructed by it has distance from r of at most d. Specifically, it's not required to minimize this distance.

You may assume that no fragment can follow directly after itself and that if fragments y and z can follow after x, then the first characters of F_y and F_z are different.

Input and output format

The first line of the input contains the number of fragments N and number of rules M. The following N lines contain one fragment F_i each. The following M lines contain 2 integers a, b (1 rule) each — it means that fragment F_b can follow directly after fragment F_a. The next-to-last line contains integers d, u, v and the last one contains the string r.

In case there's no sequence of fragments that satisfies the conditions, print one line with one integer  - 1. Otherwise, print 2 lines — the size of your sequence on the first line and this sequence, as space-separated indices of fragments, on the second one.

Note

The input files are based on real data, which means there won't be many similar fragments.

Solutions

Problem 4

Let's ignore equality signs for now — this is the same as replacing multiple consecutive identical numbers by just one copy of that number, which can't make a valid sequence invalid, and we can uniquely find out what sequence we'd get by adding the equality signs.

Take some valid sequence (not necessarily with minimal sum), and in it some number which is between signs  >  <  (or there's an end of the sequence instead of one of those signs). If it's larger than 0, we can set it to 0 and the sequence will remain valid. Notice that no other number can be 0, because it must have a smaller number next to it.

Now, what do the inequality signs tell us? If there's number a and to the right of it is a  <  sign, then the number to the right of that a must be at least a + 1. Applying mathematical induction, we can see that if we have k consecutive  >  signs and a 0 after the last one, then the number before the first  >  must be at least k; similarly for k consecutive  <  signs and a 0 before the first one.

Any number can only have 1 such sequence of identical signs after it and one before it. It's clear that if we set this number to maximum (identical  <  signs to its left,  >  to its right), then we'll get a correct original sequence. Besides, each number of this sequence is independent on the other numbers, and they're all equal to the proven lower bounds, so this sequence's sum is minimal. We win!

Counting identical signs before and after each number is easy and can be done in O(N) time. We just need to check if all numbers in the resulting sequence are  ≤ M — if they aren't, then we can output -1.

Problem 5

The optimal solution runs in 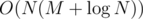time, where M is the alphabet size. My explanation of it can be found in the blog post about USACO Open. Here, we'll just show a solution that passes in the original competition.

First, let's solve this problem with an additional restriction — all M letters must occur in our chosen substring an equal number of times.

Let's assign, to each prefix [1..i] of the input string (including the empty one), an array A[i][], such that A[i][x] is the number of occurences of the (x + 1)-st letter of the alphabet in that prefix minus the number of occurences of letter a in that prefix. It's clear that we can get an equivalent array for a substring [i + 1, j] as the difference of A[j][] - A[i][]. What we want is the longest substring whose A[][x] = 0 for all x, or equivalently, A[j][] = A[i][]. It can be found by iterating over j from 1 to N and storing A[i][] for all i < j in a suitable structure (STL map<>, any hash-map...) together with the smallest index i at which they appeared; for each j, we only need to check whether an array identical to A[j][] appeared before, and if it had, the earliest index i at which it did; this gives us at most 1 substring [i + 1, j] for each j, and we only need to pick the longest one (or say that it doesn't exist). When incrementing j, we also need to update A[][x] — either by incrementing A[][s[j] - 1] (if s[j] ≠ a) or by decrementing all A[][x] (otherwise).

So, what to do when we can choose any subset of letters? Try all subsets of letters, of course :D. Just run the algorithm above while considering each subset; letters not in it can be handled as "if you see this letter, clear the map" (e.g. don't consider substrings containing it) and you can re-number the letters in that subset into 1..L for slightly better performance. The subtracted letter won't be a now, but the letter with number 1; this also solves the problem of "what if a isn't in our subset?".

Time complexity: with a fixed subset of size L and using a map<>, 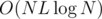, since comparing (and updating) arrays takes O(L) time. Over all subsets of size  ≤ L, it's 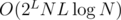; we can get rid of the log-factor using hashes. In this case, it's sufficient, since L ≤ 8 and smaller N is used for larger L.

Problem 6

This is by far the hardest problem of the three. Taking advantage of the fact that real data are used, so there won't be any evil cases, we can make an algorithm that runs in much better time than could be expected from its asymptotic complexity (up to 1 second on each test case).

We're doing a DP on states (current distance remaining d, last added fragment, position i in the target string). (d from the problem statement is retconjured to D :D) If such a state is reachable, we're able to construct a sequence starting with the given start-fragment and ending with the "last added" one, such that its distance from prefix r[1..i] is at most D - d, and we remember some state from which we were able to get to this one.

Suppose we're adding a fragment f of length l to such a state; this way, we can only reach fragments with the second parameter being f, so we just need to find out what the other 2 could be. We can do another DP for that — this time on states (distance remaining, position j in f, position i in r). From each such state, we have several possibilities:

• if r[i] = f[j], the characters match; we can happily reach the state with (the same distance remaining, j + 1, i + 1)

• if j > l, we've processed all characters of f and reached a state (distance remaining d, f, i) in the original DP

• if we have distance remaining at least 1, we can decrease it by 1 and use 1 change, moving to

  • i + 1 without changing j — equivalent to removing a character from r (in case i isn't at the end of r)
  • j + 1 without changing i — adding a character (f[j]) to r
  • j + 1, i + 1 — changing r[i] to match f[j]

This could be very slow for larger inputs — just 1 such DP has O(DlR) states! (R denotes the length of r.) But we can again use that D is small — we already know that states where |j - (i - i₀)| > D (i₀ is the i at which we started matching this fragment) can't be reached at all, which gives us just O(D²l) states. We could remember them not as (d,j,i), but (d,j,j - (i - i₀)), from which i can be re-calculated.

What's the total complexity? For each state (d,f,i), it takes O(D²l); there are O(DNR) such states (of the first DP) in total, and we can move along the M given rules (edges of a graph) to other states in O(D²L) time (L is the maximum length of a string in the input); since for all states with given d and i, there are M rules, the total worst-case omplexity is O(D³MRL).

That's obviously too much. But since the fragments aren't very similar and D is small, there'll be just very few actually reachable states; we can only do DP by keeping them in a queue (imagine that they're vertices traversed in a BFS). That could still come out too slow, though. A good optimization in this case is keeping the reachability of states of the second DP for given d and j as bits of an int and using bitwise operations on them if possible.

The last part is reconstructing the answer. If we have a final state, then we can reconstruct a sequence of states from the starting one to it; this sequence includes fragments in the order of placing them, which is what we were asked to find.

Originally, the memory limit for all problems was 1 GB.