andu9's blog

Old District Round Problem from Romania
By andu9, history, 19 months ago, In English

Hi. I have encountered this problem recently and didn't know how to approach it.

We want to construct compounds with these properties:

  • C has 4 links and can bond with either C, H or I
  • H can bond with C only through 1 link
  • I can bond with C only through 2 links
  • there is no atom with one or more free links

For example, H-C=C is not a compound because the middle C needs another link and the right one 2 more.

Two compounds are different if the numbers of C, H or I differ.

Now we define the mass of a compound as 5 * no. of C + 3 * no. of I + no. of H.

Task

Given 30 <= N <= 100000, find how many compounds with mass N there are with at least one C, I and H.

Example:

Input: N = 40

Output: 3

Explanation

These are the only possible compounds with mass 40:

Poza

  • Vote: I like it
  • +14
  • Vote: I do not like it

Comments Comments (2)
| Write comment?
»
19 months ago, # |
← Rev. 5   Vote: I like it +3 Vote: I do not like it

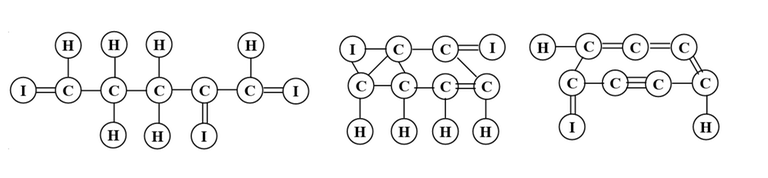
First of all, notice that the picture is a little misleading; it’s always enough to check configurations where the graph induced by the C-molecules is a chain. It’s a little tough to formally prove, but the rough idea is that this setup maximizes both the number of I-molecules that you can attach and the number of H-molecules that you can further attach (for a fixed number of I).

Another important observation is that there should be an even number of H-molecules (the sum of degrees in the graph is even).

Then, let’s fix the number $$$C$$$ of C ($$$N \geq 30$$$ implies $$$C \geq 2$$$) molecules. For each fixed $$$C$$$, you have two cases:

  1. $$$H = 0$$$: The constraints forbid that, so we can safely ignore this case.
  2. $$$H = 2 + 2H’$$$: Put two of the molecules in the endpoints. Now you have $$$C$$$ interchangeable C-molecules each of which can support either one I-molecule or one or two H-molecules. It turns out that you can attach the remaining molecules iff $$$I + 2H’ \leq C$$$. So you just need to count the number of pairs $$$(I, H’)$$$ with $$$3I + 2H’ = N - 5C - 2$$$ and $$$H’, I \geq 0$$$ and $$$I \leq C-2H’$$$. Again, see if you can derive a formula for computing that.
→ Reply