Hello Codeforces!
Thanks for participating in the round, We hope you liked the problems!
Also huge thanks to EndlessDreams for preparing the editorial.
Calculate the units first, and then calculate the value according to the units
void elysia() {
int n;cin >> n;
if(n<1024ll) cout << n << "B" << endl; else
if(n<1024ll*1024ll) cout << n/1024ll << "KiB" << endl; else
if(n<1024ll*1024ll*1024ll) cout << n/1024ll/1024ll << "MiB" << endl; else
if(n<1024ll*1024ll*1024ll*1024ll) cout << n/1024ll/1024ll/1024ll << "GiB" << endl;
}
You can compute this with fast powers, or you can compute whether n is odd or even.
void elysia() {
int n,m;
cin >> n >> m;
cout << power(245,m,10)*n%10 << endl;
}
Just simulate the problem.
Python has several tools for converting into bases and reversing strings.
for _ in range(int(input())):
n=int(input())
s=0
if bin(n)[2:]==bin(n)[2:][::-1]:
s+=1
if str(n)==str(n)[::-1]:
s+=1
if hex(n)[2:]==hex(n)[2:][::-1]:
s+=1
if s>=2:
print("ghavi")
else:
print("fanni khordim")
Obviously, the answer is equal to the longest common subsequence of the two sequences. You can reach this point by deleting all numbers except LCS.
You can then get the code by googling "LCS in n log n".
#include<bits/stdc++.h>
using namespace std;
void solve()
{
int n;
cin>>n;
vector<int> a(n+1),b(n+1),mp(n+1),f(n+1);
for(int i=1;i<=n;i++){scanf("%d",&a[i]);mp[a[i]]=i;}
for(int i=1;i<=n;i++){scanf("%d",&b[i]);f[i]=0x7fffffff;}
int len=0;
f[0]=0;
for(int i=1;i<=n;i++)
{
int l=0,r=len,mid;
if(mp[b[i]]>f[len])f[++len]=mp[b[i]];
else
{
while(l<r)
{
mid=(l+r)/2;
if(f[mid]>mp[b[i]])r=mid;
else l=mid+1;
}
f[l]=min(mp[b[i]],f[l]);
}
}
cout << 2*(n-len) << endl;
}
int main() {
int T;cin >> T;
while(T--) solve();
}
First of all, each merge causes us to lose two 1's. So if the number of 1's is odd, the merge will fail.
Second, the left and right endpoints of the string cannot be 0. Otherwise, the merge cannot be completed.
- the leftmost and rightmost 1s must be merged at the last operation, then the current goal is make the substring $$$s[2,l-1]$$$ into a 00...0 string.
Then we greedily choose the longest consecutive "1" string and merge it with the adjacent "1" string.
As long as no one consecutive "1" string is more than half the length of the total, the merge can always be completed.
void elysia() {
string t;cin >> t;
if(t=="0") {
cout << "YES" << endl;
return;
}
if(t[0]=='0'||t.end()[-1]=='0'||(int)t.size()<=2) {
cout << "NO" << endl;
return;
} else {
t.pop_back();
reverse(t.begin(),t.end());
t.pop_back();
}
vector<int> Q;int sum=0;
for(char i:t) sum+=i=='1';
for(int i=0,cnt=0;i<(int)t.size();++i) {
if(t[i]=='1') cnt++;
if(t[i]=='0'||i==(int)t.size()-1) {
if(cnt>sum/2) {
cout << "NO" << endl;
return;
}
cnt=0;
}
}
cout << (sum%2==1?"NO":"YES") << endl;
}
There are two ways to solve this problem.
1
Copy the string and evaluate the suffix array. Find the minimum value in the first half, and that's the answer.
The proof is easy. After one copy, one of the first half suffixes becomes the result of the operation, which is then done according to the suffix array definition.
#include<bits/stdc++.h>
using namespace std;
const int N = 1000010;
int n, sa[N], rk[N], oldrk[N << 1], id[N], key1[N], cnt[N];
bool cmp(int x, int y, int w) {
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
int main() {
int i, m = 127, p, w ,n;
string s;
cin >> n >> s;
n*=2;s+=s;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i-1]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1;; w <<= 1, m = p) {
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
memset(cnt, 0, sizeof(cnt));
for (i = 1; i <= n; ++i) ++cnt[key1[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[key1[i]]--] = id[i];
memcpy(oldrk + 1, rk + 1, n * sizeof(int));
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
if (p == n) {
for (int i = 1; i <= n; ++i) sa[rk[i]] = i;
break;
}
}
for(int i=1;i<=n;++i)
if(sa[i]<=n/2) {
for(int j=sa[i];j<=n/2;++j) cout << s[j-1];
for(int j=1;j<sa[i];++j) cout << s[j-1];
return 0;
}
return 0;
}
2
All strings after shift can be concatenated from two strings in the original string. To compare any two shift strings, you can use a hash and binary search to find the first distinct position and then compare.
// Code by blxst
#include <bits/stdc++.h>
#define int long long
#define fi first
#define se second
#define all(x) (x).begin(), (x).end()
using namespace std;
const int mod = 1e9 + 9;
const int key = 131;
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n;
cin >> n;
string s;
cin >> s;
s = s + s;
s = '?' + s;
vector<int> pre(2*n+5);
int res = 0;
for (int i = 1; i <= 2*n; i++) {
res = (res*key + s[i])%mod;
pre[i] = res;
}
vector<int> pow(2*n+5);
pow[0] = 1;
for (int i = 1; i <= 2*n; i++) {
pow[i] = (pow[i-1] * key)%mod;
}
auto get = [&](int l, int r) {
return (pre[r] - (pre[l-1]*pow[r - l + 1])%mod + mod)%mod;
};
auto comp = [&](int l1, int l2) {
int lf = 1;
int rg = n;
int pos = 0;
while (lf <= rg) {
int md = (lf + rg)/2;
if (get(l1, l1 + md - 1) == get(l2, l2 + md - 1)) {
pos = md;
lf = md + 1;
} else {
rg = md - 1;
}
}
if (s[l1 + pos] > s[l2 + pos]) return 1;
else return 2;
};
int ans = 1;
for (int i = 2; i <= n; i++) {
if (comp(ans, i) == 1) ans = i;
}
cout << s.substr(ans, n) << '\n';
return 0;
}
This is a dp problem.
Let $$$dp_{l,r}$$$ represent the number of methods to delete the interval $$$(l,r)$$$. We enumerate $$$x$$$ to indicate that $$$a_l$$$ and $$$a_x$$$ are eventually deleted.
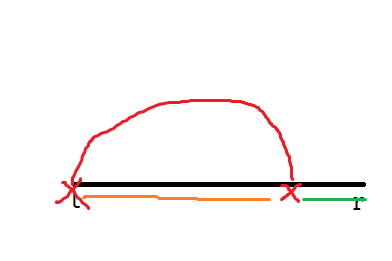
We must delete everything within $$$(l+1,x-1)$$$ before $$$a_l-a_x$$$, while $$$(x+1,r)$$$ is free to delete.
We deleted all of this with the $$$\frac{x-l}{2}$$$ step, so we have $$$\frac{x-l}{2}+1$$$ Spaces, and we just insert the $$$(x+1,r)$$$ step into these Spaces. This is the combination part.
Time complexity is $$$\Theta(n^3)$$$.
#define MOD 1000000007
int f[501][501],cntVII[502][502];
int dfs(int l,int r) {
if(l==r+1) return 1;
if(f[l][r]!=-1) return f[l][r];
int sum=0;
for(int i=l+1;i<=r;++i)
if(a[l]>a[i]&&(i-l-1)%2==0)
sum+=dfs(l+1,i-1)*dfs(i+1,r)%MOD*cntVII[(i-l+3)/2][(r-i)/2]%MOD;
return f[l][r]=sum%MOD;
}
void elysia() {
cin >> n;
for(int i=1;i<=n;++i) cin >> a[i];
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
f[i][j]=-1;
cout << dfs(1,n) << endl;
}
signed main() {
combi::init(10000,MOD);
for(int i=1;i<=501;++i)
for(int j=0;j<=501;++j)
cntVII[i][j]=combi::C(i+j-1,i-1);
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
elysia();
}










Wow! fast editorial, thanks for these nice contests.
What is the proof for $$$F$$$? I had some intutions. First, I translated this problem into an equivalent problem:
You have an array of positive integers. In one operations you select two adjacent elements, subtract $$$1$$$ from both of them. If any element becomes $$$0$$$ after this operation, remove it from the entire array, otherwise just put the remaining element back into its place. Can you remove all the elements of the entire array?
Now obviously if any element $$$a[i]$$$ exists (I call this element the "majority" element) such that $$$a[i] > sum - a[i]$$$ where $$$sum$$$ is sum of all elements of the array then clearly its not possible to remove all elements of the array.
Otherwise we will try to select adjacent element such that after applying operations the condition above (majority should exist) holds false. So obviously, after applying operation $$$sum$$$ will surely decrease by $$$2$$$ no matter what, so we will obviously try to apply operation on the maximum element $$$a[i]$$$.
However, (this is the part which I'm having confusion with) if multiple such maximums exist then we should try to apply the operation on that element whose adjacent element is also maximum (in the hope that adjacent element is also the global maximum so, we will reduce two maximums by $$$1$$$). Still, this doesn't guarantee that by following this strategy we will complete our task of deleting all the elements.
However, when I just checked the existence of majority element it simply got AC! I have no idea why this is the sufficient condition.
Great contest! Thanks to the problem setters for providing such interesting problems.
can some one explain E?
Here is an awesome blog about various approaches to this problem Lexicographically Minimal String Rotation by SPyofgame
My way of solving problem 104349E - Shift in TheForces.
Well, the first character of lex-min-shift must be minimum character.
Imagine iterating from every start. All those are candidates for the answer.
If some candidate has the next character bigger than others, then that candidate is out. Otherwise, all still present candidates keep up by having the same string.
a b . . . a b a b . . . . a bx . . . . x . x . . . . . x .> < . . . > < > < . . . . > <And now the key idea: if the candidate expands to another candidate, then he remains and the other quits.
a b . . . a b a b . . . . a b< . . . . > > < . . . . . > >That is true, from my point of view, for the following reason:
The candidate that remains will have string
[cur][cur][rest]. And the candidate that quits will have the string[cur][rest]. Those two strings have common beginning, socompare([cur][cur][rest], [cur][rest]) = compare([cur][rest], [rest]).And
[cur][rest]beats[rest], I think.Each element of string will be examined not much time, so time complexity, is fine, not more than n*log(n), maybe. If we examine a cell at point of time t, then the length of candidates is already t and we need to go through all of it by some other candidate. 1 + 2 + 4 .. k times .. <= n. So k is O(log(n))
anyone explain me the authors code for D