Есть задача timus1590. Проще говоря надо найти кол-во различных подстрок в строке. Было бы интересно услышать решение быстрее, чем O(n*n), если оно существует =).
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.11.2024 16:22:52 (l2).
Десктопная версия, переключиться на мобильную.
При поддержке
O(NlogN)
Можно решать за:
O(nlogn). Построим суффиксный массив, а вместе с ним — массив lcp, в котором будем обозначать длины наибольших общих префиксов соседних в массиве суффиксов. Тогда ответ будет таким: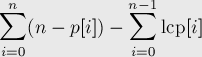
Подробнее о суффиксном массиве можно почитать на e-maxx.
O(n). Суффиксное дерево или суффиксный автомат. Можно заметить, что различные подстроки = различные пути в этих структурах. В суффиксном дереве (в "разжатом" виде) каждой подстроке будет соответствовать одна вершина. Значит, мы можем пройтись по всем рёбрам сжатого суффиксного дерева и добавлять к ответу last - first этого ребра. В суффиксном автомате можно явно посчитать кол-во путей динамикой с dfs'ом, а можно заметить, что суфф ссылки образуют суффиксное дерево перевёрнутой строки и сложить символы, которые они охватывают. Это тоже даст верный ответ.
P.S.
Строить суффиксный массив можно за O(N), искать lcp соседних суффиксов тоже — алгоритм Касаи. Почему O(NlogN)?
В принципе, можно. Но лично я не умею этого и не знаю, насколько это оправданно в плане отношения сложности написания алгоритмов и реального выигрыша во времени работы. Буду рад, если раскроешь тему.
На хабре неплохо написано.
Кстати, это, возможно, интересно. Суффиксное дерево можно построить за O(n), если иметь суффиксный массив и массив lcp. Правда, в оффлайне...
а правда, что dfs по суфдереву -> суфмас?
Ага.
Ну, если мы переходы в нём по алфавиту сортируем, а не рандомно храним.
на хабре написано про алгоритм 10-летней давности, который уже множество раз улучшили.
Сейчас есть два основных алгоритма построения суффиксного массива:
SA-IS и его улучшенная версия SACA-K, не требующая дополнительной памяти — O(n), на практике работают в 4-5 раз быстрее того, что описано у е-макса. страница автора
DivSufSort.
. Во всех статьях пишут, что работает еще в 1.5-2 раза быстрее предыдущего алгоритма, но код поистине ужасен.
Они работают быстрее на практике или для worst-case? Это разные вещи.
для SACA-K в худшем случае длина сортируемой строки на каждой итерации уменьшается в 2 раза. Проверял на строках Фибоначчи, которые близки к этому (на каждой итерации получается переход от n-й к (n-2)-й строке Фибоначчи) — все равно работает в разы быстрее qsufsort.
про DivSufSort ничего не могу сказать, кроме того что написано здесь
double post
Delete