RCC 2014 WarmUp Analysis

417A - Отбор. Автор и реализация Aksenov239.

Сначала нужно заметить, что если k больше либо равно, чем n·m, то ответ — 0. Нам осталось набрать n·m - k человек. Есть три способа их набрать:

Взять раунды только первого типа: $\text{[math]}$ .
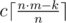Взять чуть раундов второго типа до числа, делящегося на n: $\text{[math]}$ .
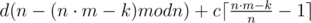Взять только раунды второго типа: d(n·m - k).

Также в данной задаче можно было написать переборное решение — сколько мы берём раундов первого типа, и сколько раундов второго.

Код: 6396283

417B - Сбой. Автор и реализация Aksenov239.

Заведём массив a на 10⁵ элементов, изначально заполненный - 1, и в ячейке с номером k будем хранить максимальный номер посылки k-го участника, который сейчас есть. Будем обрабатывать посылки последовательно. Пусть обрабатывается посылка x k. Если a[k] < x - 1, то очевидно, что ответ NO, иначе обновляем массив — a[k] = max(a[k], x).

Код: 6396297

418A - Футбол. Автор и реализация Aksenov239.

Представим турнир себе как граф. Из каждой вершины ровно k выходящих рёбер. Тогда всего nk рёбер. В полном графе максимум 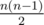$\text{[math]}$ рёбер, поэтому если n < 2k + 1, тогда ответ - 1. Иначе, соединим i-ую вершину с i + 1, ..., i + k, зациклим если нужно.

Код: 6396331

418B - Хитрый Гена. Автор и реализация Aksenov239.

Давайте отсортируем друзей по возрастанию требуемого количества мониторов. Будем считать динамику на масках — какое минимальное число денег нужно заплатить, чтобы решить такие-то задачи, если мы взяли первых i друзей. Тогда ответ надо сравнить с ответом для i первых друзей плюс количество мониторов, которое требует i-ый друг. Не трудно заметить, что если брать друзей последовательно, то пересчитывать динамику можно как рюкзак. Время работы данного алгоритма O(nlog(n) + n2^m).

Код pashka: 6396347

418C - Квадратная таблица. Автор и реализация Aksenov239.

Давайте для любого n построим массив длины n, что сумма квадратов чисел на нём является квадратом:

Если n = 1, то берём [1].
Если n = 2, то берём [3, 4].
Если n чётно, то берём $\text{[math]}$ .
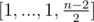Если n нечётно, то берём $\text{[math]}$ .

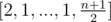Нам дано 2 числа n и m. Пусть массив a соответствует числу n, а b соответствует числу m.

Тогда итоговый массив c построим следующим способом — c_ij = a_i·b_j.

Код: 6396358

418D - Большие проблемы организаторов. Автор chavit, реализация Aksenov239.

В данной задаче есть два решения.

Первое. Подвесим за какую-нибудь вершину. Предподсчитаем для каждой, 3 самые удалённые вершины в её поддереве, а также для каждой вершины её глубину. Также предподсчитаем массивы для двоичного подъёма. Для каждой вершины i и степени двойки 2^j предподсчитаем следующие массивы — p[i][j], up[i][j] и down[i][j]. p[i][j] — это предок вершины i на расстоянии 2^j. В up[i][j] будет храниться наидлиннейший путь из i, до вершин, которые находятся в поддереве вершин, которые находятся на пути между i и p[i][j]. down[i][j] отличается от up[i][j], что хранит путь из вершины p[i][j].

Теперь осталось дело за малым. Нам приходит запрос u v, мы ищем его наименьшего общего предка — w. Осталось найти вершину hu, которая будет находиться на середине это пути. Обрезать дерево по этой вершине, и посчитать длиннейшее расстояние от вершины u в её дереве и длиннейшее расстояние от вершины v в её дереве. Представляя на дереве это, если мы не будем удалять, то можно воспользовавшись нашими предподсчитанными массивами аккуратно пересчитать значение длиннейшего пути.

Решение за O(nlog(n)).

Код: 6396376

Второе. Вкратце. Найдём диаметр этого дерева. Предподсчитаем там ответ на префиксе для каждой вершины. Тогда при ответе на запрос — мы находим, когда путь вливается диаметр. На это отрезке находим среднюю вершину, а далее отвечаем на запрос на префиксе или суффиксе.

Код cerealguy: 6396390

418E - Хитрый пароль. Авторы enot110, Aksenov239, реализация Aksenov239

Ключевая теоретическая идея данной задачи заключается в том, что 2 строка совпадает с 4, 3 с 5 и т. д. Поэтому нам нужно уметь менять что-то только на первых трёх строках.

Теперь дело остаётся за практической частью. В первую очередь сожмём все значения, чтобы они не превосходили 10⁵. Разобьём массив на отрезки длиной LEN. На каждом отрезке будем считать следующее — для каждого значения будем хранить сколько раз он встречался на префиксе cnt, а так же дерево Фенвика, в котором в ячейке f[k] будет храниться количество чисел на данном префиксе, встречающихся ровно k раз. Несложно заметить, что в первом массиве хранится ответ на запросы ко второй строке, а чтобы получить ответ для третьей строки, нужно посчитать f[cnt[k]... 10⁵]. Понятно так же, как делать пересчёт данной динамики.

Итого, получаем время на запрос за 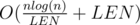$\text{[math]}$ . Если мы возьмём 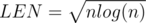$\text{[math]}$ , то время ответа на запрос составит $\text{[math]}$ .

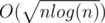Код: 6396412

Комментарии (51)

Показать архивные | Написать комментарий?

lisang

11 лет назад, # |

Дайте пожалуйста права на просмотр кода.

→ Ответить

xDEMONx

Если на Java писать, то ограничения времени жестковатое.

redjohn

Можно пояснить, для чего сортировать друзей по требуемому количеству мониторов в див2D?

Aksenov239

11 лет назад, # ^ |

Смотрите. Давайте зафиксируем число мониторов, которые мы будем покупать. Тогда мы автоматически можем брать всех друзей, которые требуют меньше мониторов. Поэтому можно отсортировать друзей по этому количеству и добавлять по одному.

Вроде понял, спасибо.

caustique

Можно разбор задачи E поподробнее пожалуйста? Интуитивно очень непонятная задача. И еще там в формулах где-то явно есть баг — видимо, в сумме лишний множитель написан.

Прошу прощения. В формуле действительно есть ошибка. Какой шаг точнее повторить? Теоретический ясен?

Начиная с момента "На каждом отрезке будем считать следующее".

Еще уточни, пожалуйста, терминологию.

Например, тут "встречался на префиксе cnt" cnt вроде как индекс префикса, а тут "нужно посчитать f[cnt[k]... 10^5]" уже вроде массив. Ну и кстати почему надо суммировать на таком отрезке?

Да. cnt[k] — сколько число k встречается раз на префиксе. cnt[k] — это на самом деле число, которое стоит во второй строке. Тогда какое количество чисел во второй строке имеют тоже самое значение, что и cnt[k]. А оно именно равно количеству чисел с cnt[k], cnt[k]+1 и так далее. А так как максимальное количество встреч равно 10⁵, то от этого и такой массив.

Я понятнее объяснил, надеюсь.

Lightless

← Rev. 2 →

...

Можете отформатировать тест? Мне не очень понятно. Но судя по тому, что я вижу — ответ YES.

Уже разобрался, извините, неправильно понял условие

Egor

← Rev. 4 →

+25

Мое решение Е с асимптотикой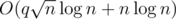 $\text{[math]}$

Будем называть число большим если оно встречается более $\text{[math]}$ Раз и маленьким в противном случае. Будем хранить для каждого большого числа дерево Фенвика с поддержкой запроса "сколько раз даннный элемент встречается на данном префиксе". Кроме того будем хранить $\text{[math]}$ Деревьев Фенвика отвечающих на вопрос сколько различных маленьких чисел встречается на префиксе не менее k раз

Тогда апдейт довольно простой — при изменениях касающихся больших чисел просто удаляем/добавляем элемент, при изменениях касающихся маленьких — пересчитываем все вхождения данного элемента в деревья Фенвика. Получаем асимптотику на запрос как указано выше

Запрос для четных строк делается втупую, для нечетных — одним запросом в соответствующее дерево Фенвика и сравнением с каждым большим числом

vlade087

+55

Nice editorial very good english!!

mathlover

+11

the problems in this contest are all very interesting.

Sammarize

В задаче div1.C про квадратную таблицу для тех, у кого нет такой математической интуиции, чтобы придумывать пример суммы n квадратов, дающих квадрат, есть другой способ. Можно обойтись простой динамикой: для каждого x от 0 до 10 000 и для каждого k от 0 до 100 вычислим can[k][x] — можно ли представить x в виде суммы k квадратов чисел, не превосходящих 100. Это очень просто пишется (6390336). После этого оказывается, например, что 10 000 можно представить в виде суммы любого количества квадратов от 1 до 100.

yeputons

Надо сказать, что чтобы искать ответ в виде c_i, j = a_i·b_j тоже нужна некоторая интуицая, с которой мне вчера не повезло. Пришлось вгонять перебор ответов вида

aaaabb
aaaabb
ccccdd
ccccdd
ccccdd

Вогналось даже на контесте: 6393584. И, да, два ифа в начале существенны, иначе не работает на каких-то тестах :)

Перед тем, как написать что-нибудь подобное, я всегда смотрю на это:

и начинаю искать более простое решение)

Я тоже так делаю. Не помогло. А сдавать надо.

Мне кажется, тебе надо было решать D, больше толку было бы =) Хотя бы из тех соображений, что ты потренировался бы решать задачи, а так ты потренировался пропихивать какой-то отстой) Да и место могло быть получше.

qwerty787788

Я вот тоже смотрел на сабмит по D на 9й минуте и искал простое решение...

Э, ну надо же смотреть не на произвольные сабмиты, а на Генины) Ну или, по крайней мере, человека, который очень редко лажает.

tyamgin

Ровно такое же решение сдал (даже константа 30 совпала). А каким образом оно не работает на этих тестах (для которых костыли)? Убрал их — что-то выводит.

Там не работает на каких-то конкретных, в стиле 42x83 и <что-то-еще>x62. Я просто на всех тестах запустил и подкостылил, где падало.

ashu1461

How to solve div1C ??

monkey.master

+13

Here's the trick: if an integer p can be written as the sum of the square of n integers, then p² can also be written as the sum of the square of n integers. For example, if

p = a₁² + a₂² + a₃²,

then

p² = (a₁² + a₂² + a₃²)² = (a₁² + a₂² - a₃²)² + (2a₁a₃)² + (2a₂a₃)².

Generally, if

p = a₁² + a₂² + ... + a_n²,

p² = (a₁² + ... + a_n - 1² - a_n²)² + (2a₁a_n)² + ... + (2a_n - 1a_n)².

So for an array of length $n$, how to make the sum of the square of its elements be a square of an integer? We can simply set a₁ = ... = a_n = 1, and the array becomes {n - 2, 2, 2, ..., 2}. Then you can apply this method to generate the matrix.

ccdd4211

yeah, from author's opinion, what we do is to generate n or m postive integers that the sum of their squares is also a square number.

andreyv

В 418C - Квадратная таблица можно обобщить последовательности таким образом:

Если n нечётное, то берём $\text{[math]}$ .
Если n чётное, то берём $\text{[math]}$ .
При малых n берём только n самых правых элементов из соответствующей последовательности.

dj3500

How to solve div1-D? We have computed p, down and up, what next?

nju_v_o_f

Problem Div1 E has a solution with complexity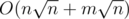 $\text{[math]}$ , just need to maintain two arrays sum1[n/Len][N], sum2[n/Len][N], where sum1[i][j] is the number of j in the first i*Len positions of row 1, and sum2[i][j] is the number of j in the first i*Len positions of row 2.

jbaramidze

Can anybody please give bit more explanation about 418B — Cunning Gena? Thanks in advance

afrizal

Consider we have dp[msk][last] = amount of min money spent on solving problems chosen on msk with hire maximum first last friends. (msk is bitmask of chosen problems)

Then suppose we want to hire the (last + 1)'s friend which cost is dp[msk][last] + cost[last + 1]. If this amount less than dp[msk|solve[last + 1]][last + 1], update it.

The answer is minimum of dp[allproblems][k] for all (1<=k<=N) plus cost of monitors required.

got it, Thanks!

But still, how do we know that optimal solution will be first k friends? why cannot it be, for example, first and fourth friends?

dont mind it

ivplay

Strange explanation to problem div1 C. Do this, you will get accepted. No explanation , no proof, why this works. there is a comment regarding this problem but that's not also enough. seems like pure math :( . this is "Code"-forces not "math"-forces. Authors should send these kinds of problem in IMOs, not here.

I think that enough information is given to understand the solution. You have to think a little, but it is a nice thing to do.

For the first part, you can manually verify that the sum of the given values squared is a square. For the second part, note that if a₁² + a₂² + ... + a_n² is a square, then (k·a₁)² + (k·a₂)² + ... + (k·a_n)² is also a square.

bezhimr

Explanation of the idea how to make such arrays is simple. If you take first n - 1 nubmers such that the sum of their squares is odd, you should suppose it equals to some 2t + 1 and make last element equal to t. Then sum of all squares will be 2n + 1 + n² = (n + 1)².

JuanMata

thanks a lot for explaining!
P.S. i think editorial should have this idea too, not just the answer!

Thanks, now its clear to me. and I agree with JuanMata , the editorial should have this idea too, not just the answer!

Swistakk

Div1-D, second solution: "Let's find the diameter of the tree. (...) Then on the query we find two distant vertices on this diameter and the path. Obviously, diameter should contain the middle of the path," There are two possibilites: 1. I don't understand what author meant. 2. This is not true. One thing is for sure — I don't understand second sentence — what are "two distant vertices" ?? Which path is third sentence about? Obviously diameter doesn't have to contain middle of every path, so I guess author meant something else.

ffao

I think he meant "every maximal path goes through at least one node in the diameter".

It's not hard to see that a path that does not go through the diameter at least once cannot be maximal, because otherwise there would be a path bigger than the diameter.

Amyc

In 417 A-Elimination, You've said: if k ≤ n·m, then the answer is equal to 0. I think it's: if n·m ≤ k, then the answer is equal to 0.

hzyfr

I just can't understand what 'realization' means...

-8

implementation

aryan29

6 лет назад, # |

54416306 why tle n^2 complexity should work according to constrains given in the problem 417C/418A

54416306 why tle I think n^2 complexity should work for problem 417C/418A according to constrains given

AryaKnight

6 лет назад, # ^ |

Heres your accepted code . https://codeforces.net/contest/418/submission/54417725

thanks

Shantanu

4 года назад, # |

I just wanna know the name of the fucker who is putting tags in the problem and putted dp 1500 tag in problem A (Elimination).

granadierfc

12 месяцев назад, # |

Could anyone explain me problem A. Very poor statements.