Hi everybody!
A new kind of contest starts today at HackerRank. The contest is named "Daily Challenge".
Each day you get to solve a problem, the difficulty increases as the week progresses. You have a weekend to solve the final problem and there will be five problems in total.
This time, I'm a writer of this contest, so I invite everybody to participate. After the contest, there will be an editorial on HackerRank.
Now the contest has started and you have about 20 hours left to solve the first, the easiest problem.










Seems like login through Google is broken
Is there going to be a "challenge" problem? I mean, there are usually lots of people who solve all the tasks in long contests, especially when full feedback is available. Or maybe some tiebreaking rules?
There should be a systest at the end of each day, so I think that getting perfect score becomes quite harder that it was.
I guess, it should be written in the rules somewhere..
Constraints in task C are crazy :) How to solve it?
i'm also interested to know the solution. :)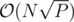 . ;)
. ;)
although i have this gut feeling that it will be
A helpful observation to make in this problem is that for every a_i and a_(i+1), at most one of these can be greater than sqrt(P). Using this with some dynamic programming gets you an O(N sqrt(P)) solution.
It's a little bit unclear how to use this observation, can you please share the details? I also have an O( N * sqrt P ) solution, but it's based on another idea.
Let W(n, x) be the number of ways to make a sequence of n more elements if the previously used element is x. Also, let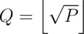 . We will find the final answer, W(N, 1), by using only W(n, x) where x ≤ Q.
. We will find the final answer, W(N, 1), by using only W(n, x) where x ≤ Q.
It should be clear that
But, we have a problem. Some of the values of i can be greater than Q. So, to fix this, we can split up the sum into two sums:
Note that this only works for x ≤ Q, but that's all we're worried about anyway. At this point it is nice to notice that W(n, x) ≥ W(n, x + 1), which is intuitive and can also be seen from above. Now, what is W(n, x) - W(n, x + 1)?
This sum can have a lot of terms, but if i > Q,
can have at most Q different values of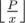 . Because of this, we can find W(n, x) - W(n, x + 1) for all the x < Q in
. Because of this, we can find W(n, x) - W(n, x + 1) for all the x < Q in 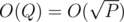 amortized time.
amortized time.
Does that explain clearly enough?
By the way, it now appears to me that my solution is sort of complicated. Do you mind sharing your solution to the problem?
Awesome, thanks.
Turned out, that your solution is almost the same with mine. I also used the idea, that there are about sqrt(P) different values of the expression [P / x] for integer x from 1 to P.
Here's my implementation: http://pastie.org/9112567
I've written a post about this on Stack Overflow
Something like this.
You can also take a look to my post which sketches a simpler solution. Are you the problem setter?
Yeah. Actually, I'm the writer of the whole contest ^^"
Until now it has been really rewarding for me, thank you, hope to see more contests from you.
Мало ли кому интересно будет решение по задаче Randomness без хешей.
Авторский разбор: https://www.hackerrank.com/blog/w1-randomness
Заведем сет отсортированных лексикографически суффиксов. Так как у нас всё рандомное, LCP'шки будут маленькие, поэтому компаратор используем самый простой: тупо сравниваем символы. Эмперически можно проверить, что максимальная LCP'шка будет ~8, для уверенности возьмем число 10.
Ну а дальше всё просто, тогда получается при изменении символа мы должны удалить 10 суффиксов из сета, поменять символ, добавить 10 суффиксов, при этом пересчитывая ответ, используя значения lcp'шек с соседними элементами в сете.
Получается что-то типа O(N * lg(N) * MAGIC + Q * lg(N) * MAGIC2) с O(n) памяти, где за MAGIC мы взяли 10. Код: http://pastie.org/private/81pidkdrdeynayxvfncaa
When the system test for the last problem will begin?
Can somebody describe his 140-pt solution to BST Maintenance?
Mine is based on centroid decomposition, but I have seen a lot of non-similar ideas in the solutions.
My solution is based on heavy-light decomposition. Let's build the final binary search tree, we can do it in O(n log n), and build heavy-light decomposition for it. Then we will add vertexes one by one. Suppose we are adding vertex u at the current step. How to calculate the distances from u to all previous vertexes? For each old vertex(v) it will be distToRoot(u) + distToRoot(v) — 2 * distToRoot(lca(u, v)). So the most difficult part is to calculate the sum of distToRoot(lca(u, v)) for all previous vertexes. It will be the sum of the sizes of subtrees for all vertexes on the path from root to u(actually except u and root). We can do it with heavy-light decomposition and segment tree for sum, with updates on the segment.
My solution is almost identical to yours, except that I computed the sums of distances in reverse order (from the last added node to the first one). This way we got an O(N * log^2(N)) solution.
I have a feeling this solution actually works in ... At least I couldn't think of counterexample.
... At least I couldn't think of counterexample.
I spent some time sharpening my solution from O(n lg^2 n) to O(n lg n) and the runtime difference is only 0.2s. I used the centroid decomposition approach. The only difference is using a linear loop instead of sorting. Weird...
I think you're right. I didn't fully analyze the time complexity. I mean, there are BSTs where, for one node, it is possible to spend O(log^2(N)) time with this approach. But summed up over all the nodes, I cannot find any example which takes more than O(N*log(N)).