I have to find min value of [a/x]+[b/x]+x-1 ,where x belongs to (1,10^9) ,here [] denotes ceil value. I then observed it is monotonic in nature. Its graph will be like 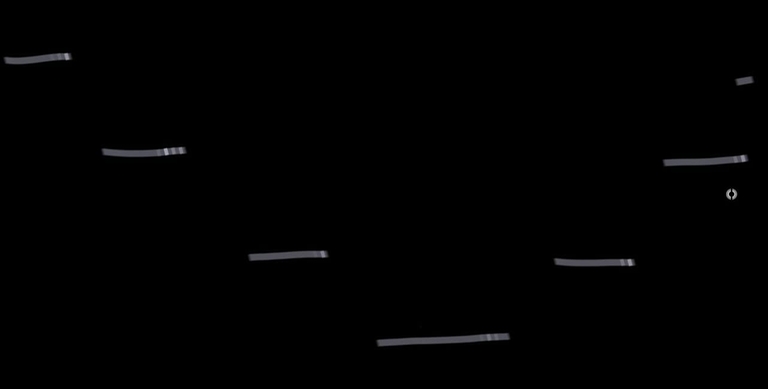
The only problem i am having is to find slope(from slope i meant if every step is assumed as points ,this will help me to shift l and r) and slope can be find by use of its previous neighbour points to find neighbour of y=f(x),we need to find length of y so for given y=[a/x]+[b/x]+x-1 i need the range of the solution










??
You can try ternary search
Where have you seen that problem? I'll gladly help you if you link the source of the problem.
https://codeforces.net/problemset/problem/1814/B
I am trying to do binary search on stepping function
You can't. It's not monotonic. The idea of the problem is that a and b is limited and by choosing x = sqrt(a+b), we find an answer that's O(sqrt(a+b)) so we can try all values up until c * sqrt(a+b) for some c and it works.
There is no method to solve stepping function using binary search?
Where length of steps varies*
You've observed something that isn't real. Check your data again.
I think graph is correct for integers
.
You forgot to add x-1.
sorry about that i forgot to match equation chatgpt fault, I have drawn some example (I am generalizing it due to my intuition ), If i am wrong give me some case where it is wrong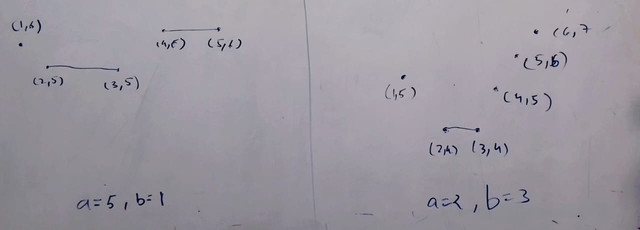
I made a python script that prints out the points where the y changes. The following is what I got for a = b = 31.
look at what happens in (7, 16), (8, 15), (9, 16), (10, 17), (11, 16). That by itself is enough.
You're suposedly a programmer, why don't you go write something really quickly to try checking your guesses for low values? I guess you're just a product of the guessing culture cultivated in recent codeforces rounds.
tfg sorry about that :(, thanks next time i will just code to check my guess(I never thought about that )
Also, you shouldn't trust ChatGPT over things related to math. It's extremely bad at it.
.
This problem can be effectively addressed using calculus, leveraging some pivotal concepts to unravel the given predicament.
1.When we differentiate an equation, we derive its slope.
2.The points of minimum or maximum correspond to instances where the slope equals zero.
3.For every point where the slope is zero:
So Now,
Applying differentiation to both sides, we arrive at y' = -[a/x^2] — [b/x^2] + 1. Upon equating y' to 0, we deduce x = √(a+b) and -√(a+b).
Subsequently, performing a secondary differentiation yields y" = 2[a/x^3] + 2[b/x^3]. When evaluating for x = √(a+b), we ascertain a minimum as y" remains positive at this point.
chatGPT is not a trustable for CP coding