1898A - Milica and String
Author: n0sk1ll
In one move, Milica can replace the whole string with $$$\texttt{AA} \ldots \texttt{A}$$$. In her second move, she can replace a prefix of length $$$k$$$ with $$$\texttt{BB} \ldots \texttt{B}$$$. The process takes no more than $$$2$$$ operations. The question remains — when can we do better?
In the hint section, we showed that the minimum number of operations is $$$0$$$, $$$1$$$, or $$$2$$$. We have $$$3$$$ cases:
No operations are needed if $$$s$$$ already contains $$$k$$$ characters $$$\texttt{B}$$$.
Else, we can use brute force to check if changing some prefix leads to $$$s$$$ having $$$k$$$ $$$\texttt{B}$$$s. If we find such a prefix, we print it as the answer, and use only one operation. There are $$$O(n)$$$ possibilities. Implementing them takes $$$O(n)$$$ or $$$O(n^2)$$$ time.
Else, we use the two operations described in the hint section.
A fun fact is that only one operation is enough. Can you prove it?
1898B - Milena and Admirer
Author: OutrunMyGun & n0sk1ll
Try a greedy approach. That is, split each $$$a_i$$$ only as many times as necessary (and try to create almost equal parts).
We will iterate over the array from right to left. Then, as described in the hint section, we will split the current $$$a_i$$$ and create almost equal parts. For example, $$$5$$$ split into three parts forms the subarray $$$[1,2,2]$$$. Splitting $$$8$$$ into four parts forms the subarray $$$[2,2,2,2]$$$. Notice that the subarrays must be sorted. Because we want to perform as few splits as possible, the rightmost endpoint value should be as high as possible (as long as it is lower than or equal to the leftmost endpoint of the splitting of $$$a_{i+1}$$$ if it exists).
When we iterate over the array, it is enough to set the current $$$a_i$$$ to the leftmost endpoint of the splitting (the smallest current value). It will help to calculate the optimal splitting of $$$a_{i-1}$$$. For the current $$$a_i$$$, we want to find the least $$$k$$$ such that we can split $$$a_{i-1}$$$ into $$$k$$$ parts so the rightmost endpoint is less than or equal to $$$a_i$$$. More formally, we want $$$\lceil \frac{a_{i-1}}{k} \rceil \leq a_i$$$ to hold. Afterwards, we set $$$a_{i-1}$$$ to $$$\lfloor \frac{a_{i-1}}{k} \rfloor$$$ and continue with our algorithm. The simplest way to find the desired $$$k$$$ is to apply the following formula:
The answer is the sum over all $$$k-1$$$.
There are $$$q \leq 2\cdot 10^5$$$ queries: given an index $$$i$$$ and an integer $$$x>1$$$, set $$$a_i := \lceil \frac{a_i}{x} \rceil$$$. Modify the array and print the answer to the original problem. Please note that the queries stack.
1898C - Colorful Grid
Author: n0sk1ll
The solution does not exist only for "small" $$$k$$$ or when $$$n+m-k$$$ is an odd integer. Try to find a construction otherwise.
Read the hint for the condition of the solution's existence. We present a single construction that solves the problem for each valid $$$k$$$.
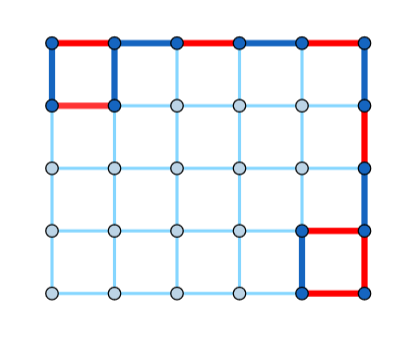
One can verify that the pattern holds in general.
How would you write a checker? That is, how would you check that a valid walk of length $$$k+1$$$ exists in the given grid (with all the edges colored beforehand)?
1898D - Absolute Beauty
Author: n0sk1ll
If $$$a_i > b_i$$$, swap them. Imagine the pairs $$$(a_i,b_i)$$$ as intervals. How can we visualize the problem?
The pair $$$(a_i,b_i)$$$ represents some interval, and $$$|a_i - b_i|$$$ is its length. Let us try to maximize the sum of the intervals' lengths. We present three cases of what a swap does to two arbitrary intervals.



Notice how the sum of the lengths increases only in the first case. We want the distance between the first interval's right endpoint and the second interval's left endpoint to be as large as possible. So we choose integers $$$i$$$ and $$$j$$$ such that $$$i \neq j$$$ and $$$a_j - b_i$$$ is maximized. We add twice the value, if it is positive, to the original absolute beauty. If the value is $$$0$$$ or negative, we simply do nothing.
To quickly find the maximum of $$$a_j - b_i$$$ over all $$$i$$$ and $$$j$$$, we find the maximum of $$$a_1,a_2,\ldots a_n$$$ and the minimum of $$$b_1,b_2, \ldots b_n$$$. Subtracting the two extremum values produces the desired result.
How to handle point updates? (change a single value in either $$$a$$$ or $$$b$$$, and print the answer after each query.)
1898E - Sofia and Strings
Author: OutrunMyGun
Notice how sorting only the substrings of length $$$2$$$ is enough. Try a greedy approach.
We sort only the substrings of length $$$2$$$. We can swap two adjacent characters if the first is greater than or equal to the second. Let us fix some character $$$s_i$$$ and presume we want to change its position to $$$j$$$. We have to perform the described swaps if they are possible. More formally:
- if $$$j<i$$$, then every character in the segment $$$s_j s_{j+1} \ldots s_{i-1}$$$ must be greater than or equal to $$$s_i$$$;
- if $$$i<j$$$, then every character in the segment $$$s_{i+1} s_{i+2} \ldots s_j$$$ must be smaller than or equal to $$$s_i$$$.
We want to reorder the string $$$s$$$ and get the string $$$s'$$$. Then, we check if we can delete some characters in $$$s'$$$ to achieve $$$t$$$. In other words, we want $$$t$$$ to be a subsequence of $$$s'$$$. A general algorithm that checks if the string $$$a$$$ is a subsequence of the string $$$b$$$ is as follows. We iterate through $$$a$$$, and for each character, we find its first next appearance in $$$b$$$. If such a character does not exist, we conclude that $$$a$$$ is not a subsequence of $$$b$$$. If we complete the iteration gracefully, then $$$a$$$ is a subsequence of $$$b$$$. We will try to check if $$$t$$$ is a subsequence of $$$s$$$, but we allow ourselves to modify $$$s$$$ along the way.
We maintain $$$26$$$ queues for positions of each lowercase English letter in the string $$$s$$$. We iterate through the string $$$t$$$, and for every character $$$t_i$$$, we try to move the first available equivalent character in $$$s$$$ to position $$$i$$$. In other words, at every moment, the prefix of string $$$s$$$ is equal to the prefix of string $$$t$$$ (if possible). For the current character $$$t_i$$$ and the corresponding $$$s_j$$$, prefixes $$$t_1t_2\dots t_{i-1}$$$ and $$$s_1s_2\dots s_{i-1}$$$ are the same, which means that $$$j\geq i$$$. To move $$$s_j$$$ to position $$$i$$$, we need to delete all characters between $$$s_i$$$ and $$$s_j$$$ that are smaller than $$$s_j$$$. We will delete them and all characters from the current prefix $$$s_1s_2\dots s_{i-1}$$$ from the queues because they are no longer candidates for $$$s_j$$$. By doing so, $$$s_j$$$ will be the first character in the corresponding queue. If at some moment in our greedy algorithm, the queue we are looking for becomes empty, then the answer is "NO". Otherwise, we will make the prefix $$$s_1s_2\dots s_m$$$ equal to the $$$t$$$ and delete the remaining characters from $$$s$$$.
Why is this greedy approach optimal? Let's suppose for some character $$$t_{i_1}$$$ we chose $$$s_{j_1}$$$ and for $$$t_{i_2}$$$ we chose $$$s_{j_2}$$$, such that $$$i_1< i_2$$$, $$$j_1>j_2$$$ and $$$t_{i_1}=t_{i_2}=s_{j_1}=s_{j_2}$$$. We need to prove that if we can move $$$s_{j_1}$$$ to position $$$i_1$$$ and $$$t_{i_2}$$$ to position $$$i_2$$$, when we can move $$$s_{j_2}$$$ to $$$i_1$$$ and $$$s_{j_1}$$$ to $$$i_2$$$. In the moment when we chose $$$s_{j_1}$$$, prefixes $$$t_1t_2\dots t_{i_1-1}$$$ and $$$s_1s_2\dots s_{i_1-1}$$$ are the same, so $$$j_1\geq i_1$$$. Similarly, $$$j_2\geq i_2$$$, which means the only possibility is $$$i_1<i_2\leq j_2<j_1$$$.
If we can move $$$s_{j_1}$$$ to position $$$i_1$$$, than we can also move $$$s_{j_2}$$$ to $$$i_1$$$ because $$$s_{j_1}=s_{j_2}$$$ and $$$j_2<j_1$$$. Also, if we can move $$$s_{j_1}$$$ to $$$i_1$$$, than we can move $$$s_{j_1}$$$ to $$$i_2$$$ because $$$i_1<i_2$$$, from which it follows that we can move $$$s_{j_2}$$$ to $$$i_2$$$, because $$$s_{j_2}=s_{j_1}$$$ and $$$j_2<j_1$$$.
The overall complexity is $$$O(\alpha \cdot (n+m))$$$, where $$$\alpha$$$ is the alphabet size ($$$\alpha=26$$$ in this problem).
Solve the problem when the size of the alphabet is arbitrary (up to $$$n$$$).
1898F - Vova Escapes the Matrix
Author: n0sk1ll
To solve the problem for matrices of $$$3$$$-rd type, find the shortest path to $$$2$$$ closest exits with a modification of BFS. Block all cells not belonging to the path with obstacles.
For a matrix of type $$$1$$$, Misha can block all empty cells (except the one Vova stands on).
For a matrix of type $$$2$$$, Misha finds the shortest path to some exit with a single BFS and then blocks every other cell.
Matrices of type $$$3$$$ are more complicated. We want to find two shortest paths to the two closest exits and block the remaining empty cells.
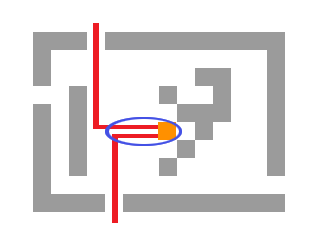
But, notice how the paths will likely share their beginnings. We do not have to count those cells twice. Let's take a look at the junction where the two paths merge. If we first fix the junction, finding the shortest path to Vova can be done by running a single BFS and precalculating the shortest distances from each cell to Vova. Finding the shortest path from the junction to the two closest exits can also be done with BFS and precalculation. We modify the BFS, making it multi-source, with a source in each exit. Also, we will allow each cell to be visited twice (but by different exits). We will need to maintain the following data for each cell:
- How many times was it visited;
- The last exit/source that visited it;
- The sum of paths from all exits/sources that visited the cell so far.
Running the BFS with proper implementation produces the answer. When everything said is precalculated, we fix the junction in $$$O(nm)$$$ ways (each empty cell can be a valid junction), and then calculate the shortest path from Vova to the two closest cells in $$$O(1)$$$ per junction.
Total complexity is $$$O(nm)$$$.
Solve the problem with LCA, or report that such a solution does not exist.










Lightning speed editorial!
Thanks for the greatly balanced round !
The bonus problems don't have a tutorial?
Hello! Can someone explain the bug in my code at this submission? I really can't find it after spending hours on it and it's really annoying me. Thanks!
233462452
I think this is a breaking testcase: NIL (sorry false statement, but it was what broke my code which failed on testcase 3 also)
Here is a test case that fails:
Your code outputs 3, but the correct answer should be 2. Split the 12 into 8+4, then split the produced 8 into 4+4. After two splits, the resulting array is [4, 4, 4, 4, 5]
Even I was getting the same wrong answer. Thanks for pointing out the mistake!
Delete
Would you like to share the link please?
delete
us
Thanks for preparing the editorial beforehand! I'm seeing a pattern of this, hopefully it will be the norm soon.
E = obvious treap: 233471686
That's like using a bazooka to kill an ant
you should learn how works std::set
You are right. Often I write treap, and then realize that using set is enough
But in this problem, I used treap with implicit key, which cannot be replaced with
std::setsegtree also works good here
I knew there will be overkillers! When I was making a test solutions, I typed a segtree of 260 lines.
Great! Share your code plz
normal vectors are also good.
problem B only has around 2500-2600 solves accepted solves. Div2B shouldnt have this low solves. I didnt like this round.
i did solve B and i am still wondering why so many less solves i mean it is not that hard after all just gotta start thinking from the end of the array and working with greeedy solutin that's it
i couldnt code it
B problem -- SEE HERE
[redacted]
They are not misplaced, they allow to do a "detour" of size 2: at position (n-2, m-1) (counting from 0), you go left, then down, then right instead of just going down.
The first loop (top left) is to do cycles of 4 or multiples. And together, you can make "detours" of length 2,4,6,8,10,... By detour I mean additional steps compared to doing only n-1 + m-1 steps (the fastest trip from top left to bottom right).
Ohh yeah that makes sense. Sorry.
cant you just use top left loop for 2 also i mean only 2 additioanal sides are only added if you go downfirst
Smart idea! Going clockwise (in cycle) for "detours" that are multiple of 4, going counter clockwise for "detours" like 2 + 4*k with k being integer. We don't even need a cycle bottom right, you are right!
why B is too hard?
Because it is greedy algorithm, as I can see
Thinking about the solution (like the greedy approach) was very easy in my opinion it was the implementation that was hard and required concentration and patience
Will you add solutions in Russian?
But also thanks)
Fun fact: we wanted put this D(but with minimisation) to our div.3 as F, but tester have seen it before and we removed it :)
n0sk1ll OutrunMyGun
bro your profile picture is insane
your pic is insane too bro
bro your is also really cool
bro your profile picture is insane too, what a coincidence!
Isn't they different? Ideas are not the same. I knew for that problem before our round.
I knew about the task and informed the rest of the team, but we concluded that they were not similar enough.
imo idea for both of them is to represent given value into sum of lengths of segments
Really like the idea behind the Problem D. There was similar problem in the contest before, back then it was impossible to figure out by myself, but now I got it.
(deleted)
When I registered for this round, I thought I was registering for Div 2, not Educational
Why is this editorial downvoted? Is it because problem B is repeated (from what I've read in some comments)?
A < C < E < D < B
Observing the testing, it would be said that this time it was a rather subjective thing. Anyways, thanks for your feedback!
A < B < E < D < C
.
.
what a fantastic well-made problems ?? I'm really impressed and horribly depressed ....
why this is wrong for the first test case in problem C ?
Better question, why do you think it is correct? Can you outline the path of length 11 from the top-left corner to the bottom-right corner? Personally, I'm not able to see such a path. The closest I can see travels the left edge and then the bottom edge, and then takes a detour near the end, but the colors on the last two edges do not allow for such a detour. Can you elaborate on what path you had in mind?
Yep, I see now I missed the edge in the square of bottom right corner, thanks
Very balanced problems! (sarcasm)
didn't my favorite one.
im dumb and i apologize
B appeared as a subproblem in a different problem (https://codeforces.net/contest/1603/problem/C), and n0sk1ll even solved it during the contest (https://codeforces.net/contest/1603/submission/133683209).
Any comments from the authors?
wow such an amazing round, problem b appearing two other problems, one of them is sub-problem the other is the exact copy
Can one of the authors respond? Like, isn't it a serious accusation? Did the coordinator know about that?
n0sk1ll OutrunMyGun
I am very sad to find B in this contest is exactly same to this 2366. Minimum Replacements to Sort the Array ,a problem in LeetCode.And there are many people having Accept it but I haven't
What makes me even sadder is that I spent too much time on question B, which caused me to AC on question D one minute after the competition.
".And there are many people having Accept it but I haven't" not because you were unable to solve it means everybody who got AC had already seen the problem besides B is not that hard if you are specialist you gotta solve it iwas gray before this contest and i have solved it, besides the fact that it lost youu a lot of time is because of your bad time management
I'm gonna be honest, C was excruciatingly painful. The idea was simple but the implementation was awful.
I feel like a much more natural way to do D is as follows:
Let $$$S = \sum_\limits{i=1}^n |a_i - b_i|$$$, then a swap of two elements of $$$b$$$ at indices $$$i,j$$$ is equivalent to $$$S \to S + |a_j - b_i| + |a_i - b_j| - |a_i - b_i| - |a_j - b_j|$$$
$$$S$$$ is clearly invariant, so to maximise $$$S + |a_j - b_i| + |a_i - b_j| - |a_i - b_i| - |a_j - b_j|$$$, it suffices to maximise $$$|a_j - b_i| + |a_i - b_j| - |a_i - b_i| - |a_j - b_j|$$$.
We can iterate over $$$i$$$ and find the best $$$j < i$$$ that maximises the above, and then take max over all $$$i$$$. If we are at index $$$i$$$, then $$$|a_j - b_i| + |a_i - b_j| - |a_i - b_i| - |a_j - b_j| = |a_j - B| + |b_j - A| - C - |a_j - b_j|$$$, where $$$A,B,C$$$ are known "constants".
Then, we just need to maximise $$$|a_j - B| + |b_j - A| - |a_j - b_j|$$$. The way I thought to do this was to just use the fact that $$$x \leqslant |x|$$$, so
$$$(a_j - B) + (b_j - A) - |a_j - b_j| \leqslant |a_j - B| + |b_j - A| - |a_j - b_j|$$$
$$$(a_j - B) + (-b_j + A) - |a_j - b_j| \leqslant |a_j - B| + |b_j - A| - |a_j - b_j|$$$
$$$(-a_j + B) + (b_j - A) - |a_j - b_j| \leqslant |a_j - B| + |b_j - A| - |a_j - b_j|$$$
$$$(-a_j + B) + (-b_j + A) - |a_j - b_j| \leqslant |a_j - B| + |b_j - A| - |a_j - b_j|$$$
So I made 4 arrays that stored each type of modified element, then just took the cumulative max up to index $$$i-1$$$ (i.e. $$$\max(\text{arr}[0:i-1])$$$) of all 4 arrays at each index to find the best configuration, and added in the constants later.
233479793
(I don't think this idea works for the min variant, i.e. minimise the score when swapped)
I solved this way too
I have just upsolved problem D based on your method! Thank you for your detail explanation!
What is A B C -> "where A,B,C are known "constants".
$$$A = a_i$$$, $$$B = b_i$$$ and $$$C = |a_i - b_i|$$$, those are constant for a fixed $$$i$$$.
im dumb and i apologize
Your solution for 1898C — Colorful Grid does not work for the edge case m=2, k=(m-1+n-1)+2
3 <= m, n <= 16.
thanks. I misread and solved it for m, n >= 2 :p
The C question was retarded. If you keep an implementation question try to keep it so that atleast some good pattern shows up.
Why so many dislikes? Problems are hard but good.
I don't like the editorials. For example problem C editorial doesn't have explanation at all.
It's simple from picture, like we can rotate for %4 in first loop and only thing remaining will be remainder 2 that is handled via second loop if exist
Yeah but not everyone understands from the picture. Also they should explain how they got to the picture.
Bro I have question,why we are using mass reduction in spacecrafts wouldn't radiation pressure will be better option?
yes
So why don't we work on radiation pressure to use it on spacecrafts
idk
Problem B and D is repeated.Also a poor distribution of problems
I have a question. What did you learn from this contest guys?
Please encourage people to solve problems.
I learned a lot from C. Mainly because I thought it would be smart to use two 2-dimensional arrays to calculate the solution and then output them.
Only using one 2-dimensional array is a lot easier though. Easier to debug, easier to fill and not harder to output.
E could have been better, a little bit too detailed sample testcases for a div2E.
Can someone tell me why I got 'Idleness limit exceeded' in my submission? I couldn't get it. Thanks!
233470642
Your code is a TLE but since you are using cerr, you are getting Idleness limit exceeded.
Here it is without cerrs: 233490794
Problem E is very similar to 1187D - Subarray Sorting, the idea behind both problems are just the same, E just need one more not-so-hard-to-see observation. I just added a few lines of code and got AC: 233489174, 233489126
If you don't want to invent a new type of BFS for F but just want to use a normal BFS as a black box, you can still do it using a cool idea: we want to choose two exits and find distances from them to all points in the greed. Let's split all exits randomly into two types and run two different BFSs from the first exit and from the second exit. With probability $$$1/2$$$ our desired pair of exits will be in different groups, so we will find the answer. By repeating this process $$$T$$$ times for some constant $$$T$$$ we may bring the error probability down to $$$1/2^T$$$.
Maybe this solution can be improved to 0 error probability if we don't split exits randomly, instead we number each exit from $$$0$$$ to $$$n + m - 1$$$, then process $$$log_2(n+m)$$$ times, and for the $$$i$$$-th process, split those exits by $$$i$$$-th bit of their index. So that every pair of exits will be checked.
True, I did this in my solution and it worked, well I didn't split according to i-th bit
Oh, yes, that's great. (I guess, there are at most $$$2 \cdot (n + m) - 4$$$ exits though but whatever).
When submitting code, I observed that the speed of C's spj is very slow. Although the construction of C is indeed not difficult, I want to know how C's spj checks whether the construction scheme is correct. Does it find all the cycles? Thanks, n0sk1ll.
I am also interested in the bonus for Problem C (how to implement the checker for C).
My initial idea is to split each node into two ones (red and blue, representing the color of the last edge traversed when reaching that node).
The problem would then be transformed into: how to determine if there exists a path of length
lbetween two specified points in a cyclic undirected graph. However, I haven't found a straightforward solution to solve this problem.Solution for D
submission 233513167
Can someone help with the proof of this solution!
i generalized all cases as A1<=B2 and A2>=B1
after swapping the contribution is
(b2 - a1) + (a2 - b1) - abs(a1-b1) - abs(a2-b2)=
b2+a2-abs(a2-b2) - (b1+a1+abs(a1-b1))MAX( b2+a2-abs(a2-b2)) - MIN(b1+a1+abs(a1-b1))=> ansThe proof is almost complete.
Since the left and right terms are independent, they can be computed separately, and later combined to optimize the solution **** Think of having one loop for MAX and another for MIN. Since you want to maximize contributions, you want the to take the best combination (keeping track of max for all i).
Might be easier to grasp if you convert the MIN into a max of the negative value. See: https://codeforces.net/contest/1898/submission/233522779
There is a no brainer solution for problem D. We can use the idea from https://www.geeksforgeeks.org/maximum-value-arri-arrj-j/.
My submission:https://codeforces.net/contest/1898/submission/233490749
This contest stole some problem. It is stupid and should be unrated.
I've seen in your account that you didn't join the contest. If you don't support the writers of this contest, do not make them feel bad. They poured their heart in the contest, and they do not need to suffer more. Comment responsibly or don't comment at all. Roasting the writers is not a good thing to do and no one should do it. I love the CF community but I hope the community keeps itself in order and to punish any members that doesn't support the community.
I might get downvote for saying this but this is my alt to comment because I don't want negative contribution, my main account did join the contest, also I don't think they poured their heart in the contest(just look at the copied problem). Even if they do, what's good of poured their heart in the contest when the quality is bad.
And... look at how you support the community: https://codeforces.net/blog/entry/119772#comment-1067920
ok, that may be true, but just don't roast 'em that bad
Solution to bonus A: Only 1 operation.
Let numb be the number of letters of B in string S
Case1: if numb = k -> 0 operations needed
Case2: if numb < k -> 1 operation, iterate over every position in string, if A -> B, numb + 1 until numb = k
Case2: if numb > k -> 1 operation, iterate over string and any letter B change to A and numb-- until numb = k
Maximum 1 operation
Will be russian translations?
n0sk1ll, can you please tell why in 1898F - Vova Escapes the Matrix, it will always be optimal to find shortest path to 2 exit points in the 3rd type matrix??
Because , cannot there be a such construction of matrix where the shortest path to 2 closest exit points can flow the path in such a way that later on we will not be able to put maximum obstacles in remaining blocks ??
We will fill all the cells that are not part of at least 1 path. Therefore, we need the least amount of cells empty, but they need to form at least 2 exit paths.
I might have not understood your question correctly, if that is the case, please let me know.
NemanjaSo2005, thanks for the reply.
But, what I am asking is that how we are so sure that the shortest path to 2 closest exist points will be optimal.
Because I am thinking cannot there be such a matrix which is constructed such that , in reaching those closest points you got to fill the maximum cells in the grid later and that will not be optimal then.
And it can be rephrased also in the other way that " Cannot there be a path to some not closest points that can make the final answer optimal.(because in that unique construction of matrix the path to that not closest path is not very concentrated with initial obstacles compared to the path to closest exit points" I.e. will be able to fill out maximum cells with obstacle.
Can there such a case exist ? Because greedy have to be true for all the possible cases that's why I asked the doubt ?
NemanjaSo2005, I think my assumption will be wrong then ,the path I have said to the closest exit point will not be shortest then. And will become wrong by contradiction.
But , however can you please still clarify. It will be very helpful.
The optimal path goes from Vova's cell to some other with shortest path. From that cell, there is a divergence to 2 paths, each being shortest path to some edge. Just draw a few matrices and you can make sure yourself that it is the case.
Well B is just a leetcode problem.
Link
Thanks for the fast editorial.
greedy algorithm is so hard
How to solve F's Bonus? The graph truly look like a LCA problem but I cannot find a way to construct the tree. I have tried to construct the tree by the distance from the start point, but i failed. Cound someone give me a idea? It's better to use the following graph as an example.
Sorry for poor English expression.
Where can i attempt bonus problem??
C, i am getting this error on testcase 1:wrong answer Token parameter [name=answer] equals to "R", doesn't correspond to pattern "[Yy][Ee][Ss]|[Nn][Oo]" (test case 5)
my answer for 5th test case which is 4 4 8 is ~~~~~
YES R B R R R R B B B B B B B B B B B B B R B B R B ~~~~~
there's a path which follows. -> -> -> v v <- v ->
233730117
Check your output on the fourth test.
Any idea to solve the bonus for problem B? Thanks in advance!
Did you got the the solution for bonus part of problem B?
ELDRVD and nosk1ll , would you please tell how to solve bonus part of problem B?
I think for the bonus part of problem C , We can use meet in the middle concept.
K-(n+m) is odd or negative then no solution exit.
k-(n+m) is multiple of 6 then k = n+m+6
k-(n+m) is multiple of 4 then k = n+m+4
k-(n+m) is multiple of 2 then k = n+m+2
Now k can be at max 38.
Use meet in the middle concept here. Find number of nodes({point,last edge as red or blue}) where it can end starting from (1,1) and (n,m). And then take intersection. If null color pattern is bad, else it is good enough is have atleast one path.
how to solve bonus problem E?
Can someone intuitively explain why it's okay to swap a[i] and b[i] in problem D? I did some casework and am convinced that it is correct, but I can't wrap my head around it intuitively.
I have no idea why my solution 241233386 doesn't work for 1898D - Absolute Beauty. Please point out the issue. Thank you!
[Explanation] Let $$$S = \sum{|a_i - b_i|}$$$. This represents the initial absolute beauty. Let $$$S(i, j)$$$ denote the beauty after swapping elements at indices $$$i$$$ and $$$j$$$. We can express $$$S(i, j) = S + \delta(i, j)$$$, where
Hence, it suffices to maximize $$$\delta(i, j)$$$. Now, fixing index $$$i$$$ and considering $$$\delta(i, j)$$$ as a function of $$$j$$$, we can identify four possible expressions after removing absolute value brackets:
where $$$a_k$$$ and $$$b_k$$$ are constants. Each expression can be regarded as a linear function of the variables $$$a_j$$$, $$$b_j$$$, $$$a_j + b_j$$$, and $$$a_j - b_j$$$, respectively. Since a linear function within an interval takes its maximum at either endpoint, the candidates for $$$(a_j, b_j)$$$ to maximize $$$\delta(i, j)$$$ are at most 8. (Candidates are to maximize $$$a_j$$$, $$$b_j$$$, $$$a_j + b_j$$$, or $$$a_j - b_j$$$, or to minimize one of them). These candidates remain invariant even when iterating over $$$i$$$. Therefore, it is sufficient to iterate over $$$i$$$, check $$$8N$$$ pairs of $$$(i, j)$$$, and calculate $$$\delta(i, j)$$$ straightforwardly.
anyone can give hint for bonus problem in B
.
..